Движение заряженной частицы в электрическом и магнитном полях

Если частица, обладающая зарядом е, движется в пространстве,где имеется электрическое поле с напряжённостью E то на неё действует сила eE. Если, кроме электрического, имеется магнитное поле,то на частицу действует ещё сила Лоренца, равная e[uB] , где u - скорость движения частицы относительно поля, B - магнитная индукция. Поэтому согласно второму закону Ньютона уравнение движения частиц имеет вид: Рассмотрим частный случай, когда нет электрического поля, но имеется магнитное поле. Предположим, что частица, обладающая начальной скоростью u0, попадает в магнитное поле с индукцией B. Это поле мы будем считать однородным и направленным перпендикулярно к скорости u0,действующая на частицу сила Лоренца всегда перпендикулярна к скорости движения частицы. Это значит,что работа силы Лоренца всегда равна нулю; следовательно, абсолютное значение скорости движения частицы, а значит, и энергия частицы остаются постоянными при движении. Так как скорость частицы u не изменяется, то величина силы Лоренца остается постоянной. Эта сила, будучи перпендикулярной, к направлению движения, является центростремительной силой(при движении по кривой или по окружности-это сила,действующая на предмет таким образом, что он удерживается на круговой траектории.)

Закон Био-Савара-Лапласа для расчета магнитных полей токов

Физический закон для определения модуля вектора магнитной индукции в любой точке магнитного поля, порождаемого постоянным электрическим током на некотором рассматриваемом участке. Был установлен экспериментально в 1820 году Био и Саваром. Они провели исследования магнитных полей токов различной формы.Лаплас обобщил эти исследования.Он проанализировал данное экспериментальные данные и сделал вывод,что магнитное поле любого тока может быть вычеслено как векторная сумма(суперпозиция)полей,создаваемых отдельными элементарными участками тока. выражение и показал, что с его помощью путём интегрирования, в частности, можно вычислить магнитное поле движущегося точечного заряда, если считать движение одной заряженной частицы током. Закон Био-Савара-Лапласа для проводника с током I, элемент которого 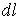создает в некоторой точкеА индукцию поля 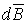записывается в ви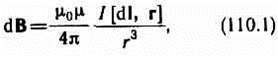де:
где 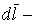вектор, по модулю равный длине 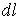проводника и совпадающий по направлению с током; 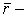радиус-вектор, проведенный от элемента 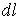проводника в точку А поля; 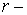модуль радиуса-вектора. Закон Био-Савара-Лапласа совместно с принципом суперпозиции позволяет рассчитывать магнитные поля, создаваемые любыми проводниками с током.

Закон Био-Савара-Лапласа: 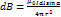,где r-расстояние от участка тока до рассматриваемой точки поля,α-угол между током и направлением в данную точку r(вектор), 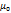–магнитная постоянная.