Волновые свойства микрочастиц. гипотеза луи де бройля
Тепловое излучение
1. Излучательная и поглощательная способность тела. АЧТ. З-ны излучения.
Тепловое излучение: 0.2×10-7¾10-3 м (ультрафиолетовое, видимое, инфракрасное).
Есть два вида излучения телами электромагнитных волн:
Тепловое - э/м излучение испускается нагретыми телами или возникает за счёт внутренней энергии тела.
Люминесценция - излучение за счёт других видов энергии (хемлюминисценция, электралюминисценция, фотолюминесценция, катодолюминесценция).
Тепловое излучение имеет особенность-единственный вид излучения, которое может находиться в равновесии с излучающим телом, т.е. быть равновесным.
Энергия ТИ и его спектральный состав, т.е. зависимость энергии от частоты определяется температурой и природой тела.
Постоянство температуры нагретого тела можно обеспечить двумя способами: 1) притоком энергии извне; 2) поглощение телом энергии из окружающего пространства.
Если 2-й случай - тело находится в состоянии термодинамического равновесия, и спектральный состав зависит только от температуры.
Термодинамическое равновесие носит динамический характер.
Eпоглощения=Eизлучения- правило Прево
Источником равновесного излучения может служить замкнутая полость со стенками не проводящими тепла и поддерживаемая при постоянной температуре.
1.2 Характеристики теплового излучения {к: 3-5}
1) Спектральная испускательная способность (испуск. способность):
СИС ¾ энергия, испускаемая в единицу времени единичной площадкой в единичном интервале частот: r(w,T)=dE/(dtdSsw)
2) Интегральная испускательная способность (аналитическая светимость):
ИИС ¾ поток энергии, испускаемый единичной площадкой во всех направлениях в пределах < 2p : R(T)=or(w,T)dw {0, ?}
Излучение может характеризоваться как w так и l. Участку спектра dw соответствует dl: w=(2pc)/l ;dw=[(-2pc)/l2]dl
Если dw и dl соответствуют одному и тому же участку спектра, то выполняется соотношение: r(w, T)dw = r ’(l,T)dl
Т.о.: r(w, T)=r’(l,T)?(l2/2pc)
3) Поглощательная способность:
ПС ? отношение потока энергии, поглощаемого элементарной площадкой к падающему на неё потоку: a(w, T)=dФ’/dФ
dФw- поток, заключённый в dw ; a(w, T)?1
Тело, полностью поглощающее все падающие на него потоки ? Абсолютно Чёрное Тело (АЧТ) (a=1)
Существует максимально возможное количество энергии, испускаемое при данной температуре. Источник -АЧТ.
АЧТ в природе не существует.
Устройством, моделирующим АЧТ, является вогнутая полость с отверстием и непроницаемыми стенками с некоторой постоянной температурой.
Излучение АЧТ - равновесное.
2. Закон Стефана-Больцмана. Вина.
Попытки найти аналитический вид f(  ,T) или U(
,T) или U(  ,T) привели к установлению рада законов теплового излучения:
,T) привели к установлению рада законов теплового излучения:
Закон Стефана-Больцмана .На основе экспериментальных данных Стефан ошибочно предположил, что R ~ T4 (в 1879).В 1884 Больцман выяснил, что это справедливо только для АЧТ.
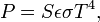
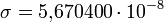 Дж·с−1·м−2 · К−4.
Дж·с−1·м−2 · К−4.
Закон смещения Вина
На основе т/д соображений и э/м теории немецкий физик Вин в 1893 году нашёл общий вид функции распределения энергии по частотам в спектре излучения АЧТ: f(  ,T)= λ 3F(λ,T);
,T)= λ 3F(λ,T);
j( λ,T)=[(2пc)/ λ]3×F[(2пc)/  T] × [(2пc)/ λ 2] Как следует из приведённых выражений, при изменении температуры вид f(λ, T) и j( λ, T) сохраняется в смещённой шкале частот.
T] × [(2пc)/ λ 2] Как следует из приведённых выражений, при изменении температуры вид f(λ, T) и j( λ, T) сохраняется в смещённой шкале частот.
Отсюда следует название закона.
Положение максимума этих функций удовлетворяет условию:
λmax/T=const ;
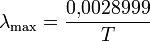
закон смещения Вина; м\к ¾ постоянная Вина.Закон Рэлея-Джинса
Для получения явного вида 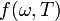 необходимо обратиться к конкретной модели излучения.С точки зрения классической теории АЧТ можно представить как совокупность осцилляторов, совокупная энергия которых ~ квадрату амплитуды колебаний и непрерывно меняется.Равновесное излучение в полости можно представить как совокупность стоячих волн различных частот, количество которых в единице объёма:
необходимо обратиться к конкретной модели излучения.С точки зрения классической теории АЧТ можно представить как совокупность осцилляторов, совокупная энергия которых ~ квадрату амплитуды колебаний и непрерывно меняется.Равновесное излучение в полости можно представить как совокупность стоячих волн различных частот, количество которых в единице объёма:
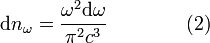
Рэлей и Джинс попытались установить аналитический вид f(  ,T), опираясь на
,T), опираясь на 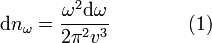
и исходя из теоремы равномерном распределении энергии по степеням свободы.
Они предположили, что на каждую стоячую волну в среднем приходится энергия 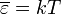 (по 1/2 на электрическую и магнитную составляющие).
(по 1/2 на электрическую и магнитную составляющие). 
Отсюда следует вид U(  ,T):
,T):
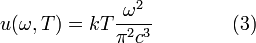
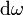 интервал частот
интервал частот
Вывод формулы Рэлея-Джинса безупречен с классической позиции, но он удовлетворяет экспериментальным данным только на малых частотах.
Закон Рэлея-Джинса
Для получения явного вида 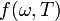 необходимо обратиться к конкретной модели излучения.
необходимо обратиться к конкретной модели излучения.
С точки зрения классической теории АЧТ можно представить как совокупность осцилляторов, совокупная энергия которых ~ квадрату амплитуды колебаний и непрерывно меняется.
Равновесное излучение в полости можно представить как совокупность стоячих волн различных частот, количество которых в единице объёма:
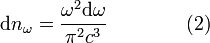
Рэлей и Джинс попытались установить аналитический вид f(  ,T), опираясь на
,T), опираясь на 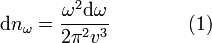
и исходя из теоремы равномерном распределении энергии по степеням свободы.
Они предположили, что на каждую стоячую волну в среднем приходится энергия 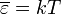 (по 1/2 на электрическую и магнитную составляющие).
(по 1/2 на электрическую и магнитную составляющие).  Отсюда следует вид U(
Отсюда следует вид U(  ,T):
,T):
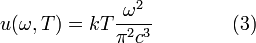
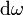 интервал частот
интервал частот
Вывод формулы Рэлея-Джинса безупречен с классической позиции, но он удовлетворяет экспериментальным данным только на малых частотах
ФОРМУЛА ПЛАНКА
В 1900 году Планку удалось отыскать вид f(  ,T), который удовлетворял опыту во всех диапазонах частот.
,T), который удовлетворял опыту во всех диапазонах частот.
Была выдвинута гипотеза, что энергия испускается в виде отдельных порций, величина которых ~ h  =
= 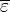 ;
;
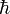 = 1.054 · 10−27эрг·с.Размерностьh совпадает с “размерностью действия” (энергия × время) => постоянная Планка называется квантом действия.
= 1.054 · 10−27эрг·с.Размерностьh совпадает с “размерностью действия” (энергия × время) => постоянная Планка называется квантом действия.
Из постулатов Планка следует, что если э/м излучение испускается порциями h  , то его энергия кратна этой величине.
, то его энергия кратна этой величине.
Математически это означает дискретность => нужно применять суммирование, а не интегрирование.
< 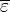 >=ЕnPn, Pn¾ вероятность того, что Е колебания с
>=ЕnPn, Pn¾ вероятность того, что Е колебания с  имеет значение Еn ;
имеет значение Еn ;
В состоянии равновесия распределение колебаний по значениям энергии подчиняется закону Больцмана:
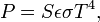
Среднее значение энергии колебаний частоты  равно:
равно:
; 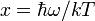 Допустим, что
Допустим, что  (и x) изменяется непрерывно:
(и x) изменяется непрерывно:
средняя 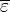 , приходящаяся на степень свободы, не одинакова для разных частот стоячих волн.
, приходящаяся на степень свободы, не одинакова для разных частот стоячих волн.
< 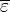 >=kT;
>=kT;
С ростом  средняя Е убывает => интеграл светимости сходится.
средняя Е убывает => интеграл светимости сходится.
U(  , T)d
, T)d  =<Е>/[
=<Е>/[  2/(п2c3)]d
2/(п2c3)]d 
Из формулы Планка следует:
1) Закон Рэлея-Джинса ( 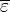
 <<kT):...
<<kT):...
f(  , T)=[
, T)=[  2/(4п2c2)]\kT;
2/(4п2c2)]\kT;
2) Закон излучения Вина ( 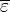
 >>kT):
>>kT):
f(  , T)=[(
, T)=[( 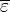
 3)/(4п2c2)]e-hw/kT);
3)/(4п2c2)]e-hw/kT);
3) Закон Стефана-Больцмана:
4) 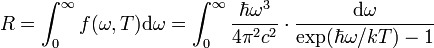 Закон смещения Вина:
Закон смещения Вина:
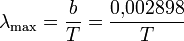
Таким образом формула Планка описывает все свойства равновесного теплового излучения.
5.Фотоэффе́кт — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
ЗАКОНЫ ФОТОЭФФЕКТА
1) При неизменном спектральном составе света сила тока насыщения пропорциональна падающему световому потоку: Iн ~ Ф
2) Начальная кинетическая энергия линейно растёт с увеличением частоты и не зависит от интенсивности: m  2max/2=
2max/2= 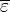 Uз ;
Uз ;
3) Существует минимальная частота (  minили λmax), характерная для каждого металла, начиная с которой фотоэффект не происходит.
minили λmax), характерная для каждого металла, начиная с которой фотоэффект не происходит.
 min¾ красная граница
min¾ красная граница
6. Внешний фотоэффект по Энштейну. Установленные экспериментально зависимости не могли быть объяснены. Все особенности фотоэффекта объяснил в 1905м году Эйнштейн ¾ “свет поглощается тоже квантами”.
Используя гипотезу квантов, он вывел формулу: 
 =Aвых + Ekmax
=Aвых + Ekmax
Ekmax = m  2max/2 ,
2max/2 ,  << c ; Ek = E-E0 ,
<< c ; Ek = E-E0 ,  ~ c
~ c
Ekmax = Ekmax (  );y=kx-b;
);y=kx-b;
Мы рассматриваем однофотонный фотоэффект при малых световых потоках: квант поглощается одним электроном.
Мощные лазеры дают многофотонный фотоэффект.
В полупроводниках и диэлектриках имеет место внутренний фотоэффект.
Для объяснения законов теплового излучения Планк предположил, что электромагнитное излучение испускается квантами. Для объяснения фотоэффекта Эйнштейн предположил поглощение квантами.Он же предположил, что электромагнитное излучение распространяется квантами => оно ¾ совокупность фотонов, а классическое представление об электромагнитном поле оказывается верным лишь для предельного случая (число фотонов велико).
Подтверждающий эксперимент ¾ опыт Ботэ.
Слабое рентгеновское излучение падает на фольгу, которая становится источником вторичного излучения (флуоресценция), которое попадает на счётчик => отметка на ленте.
Если бы излучаемая энергия распределялась равномерно, то отметки на ленте были бы симметричны. Беспорядок отметок => дискретные частицы (фотоны).
Точная теория электромагнитного поля, как поля квантованного, ¾ называется квантовой электродинамикой, согласно которой движение фотонов не может быть описано без учёта волновых свойств.Соотношения между волновыми и корпускулярными свойствами можно выяснить по распределению интенсивности освещения экрана.
I ~ A2 (волновое представление)
Согласно корпускулярному представлению ¾I ~ плотности потока фотона.Количество фотонов, регистрируемое фотоумножителем, ¾ случайное в данной точке => вероятность обнаружения фотона в пределах dV определяется выражением: dP=cA2dV, c¾ коэффициент пропорциональности
Эффект Комптона
1923 ¾ рассеивающее вещество в рентгеновском излучении содержит кроме исходного (с λ) излучение и с большей λ’ ,
причём D λ = λ’- λ = λc(1-cos α) ¾ зависит только от угла α между начальным пучком и направлением рассеивания и не зависит от λ и типа вещества: λc= 0.0243 Ao = const;
Эффект Комптона объясняется как эффект упругого рассеивания фотонов на практически свободных внешних (валентных) электронах атомов рассеивания.
В этом процессе выполняются законы сохранения энергии и импульса.
P=mc=(E/c2)c = E/c = 
 /c =
/c =  2п/ λ =k
2п/ λ =k  ; P=
; P=  k ;
k ;
Фотоны имеют нулевую массу покоя, как и все частицы,
движущиеся с C;
ЗСЭ: 
 +mc2=
+mc2= 
 ’+c\sqrt(p2+m2c2) ; ЗСИ:
’+c\sqrt(p2+m2c2) ; ЗСИ:  k=
k=  k+Pe ;
k+Pe ;  =kc;
=kc;
p2=  2(k2-k’2-2kk’)+2mc(k-k’)
2(k2-k’2-2kk’)+2mc(k-k’)  ;
;
λ’- λ =[(2п  )/(mc)]\(1-cos α);
)/(mc)]\(1-cos α);
λc=(2п  )/(mc)=h/mc¾ комптоновская длина волны для частицы
)/(mc)=h/mc¾ комптоновская длина волны для частицы
массой m (тут ¾ для e¾);
Полученная формула согласуется с экспериментом.
Замечание: фотон не может передать часть энергии электрону в поле ядра, т.к. это квант (неделимая порция энергии) => рассеивание следует рассматривать как цепочку событий.
1) Поглощение фотона электроном, слабо связанным с атомом.
2) Изменение состояния электрона (образование виртуального электрона).
3) Испускание этим электроном другого фотона под углом α к начальной траектории.
Фотон не может передать всю свою энергию электрону, иначе нарушится ЭСИ и ЗСЭ
8.Бо́ровскаямоде́льа́тома (Моде́льБо́ра)
Атом может находиться только в особенных стационарных, или квантовых, состояниях, каждому из которых отвечает определенная энергия. В стационарном состоянии атом не излучает электромагнитных волн.Излучение и поглощение энергии атомом происходит при скачкообразном переходе из одного стационарного состояния в другое, при этом имеют место два соотношения: 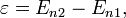 где
где  — излучённая (поглощённая) энергия,
— излучённая (поглощённая) энергия, 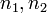 — номера квантовых состояний. В спектроскопии
— номера квантовых состояний. В спектроскопии 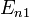 и
и 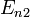 называются термами.Правилоквантованиямомента импульса:
называются термами.Правилоквантованиямомента импульса: 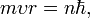
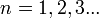 Далее исходя из соображений классической физики о круговом движении электрона вокруг неподвижного ядра по стационарной орбите под действием кулоновской силы притяжения, Бором были получены выражения для радиусов стационарных орбит и энергии электрона на этих орбитах:
Далее исходя из соображений классической физики о круговом движении электрона вокруг неподвижного ядра по стационарной орбите под действием кулоновской силы притяжения, Бором были получены выражения для радиусов стационарных орбит и энергии электрона на этих орбитах: 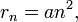
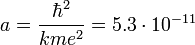 м — боровский радиус.
м — боровский радиус. 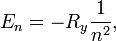
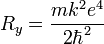 — энергетическая постоянная Ридберга (численно равна 13,6 эВ).Движение электрона вокруг атомного ядра в рамках классической механики можно рассматривать как «линейный осциллятор», который характеризуется «адиабатичным инвариантом», представляющим собой площадь эллипса (в обобщенных координатах):
— энергетическая постоянная Ридберга (численно равна 13,6 эВ).Движение электрона вокруг атомного ядра в рамках классической механики можно рассматривать как «линейный осциллятор», который характеризуется «адиабатичным инвариантом», представляющим собой площадь эллипса (в обобщенных координатах):
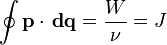
где — 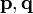 — обобщенный импульс и координаты электрона,
— обобщенный импульс и координаты электрона, 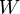 — энергия,
— энергия,  — частота. А квантовый постулат утверждает, что площадь замкнутой кривой в фазовой
— частота. А квантовый постулат утверждает, что площадь замкнутой кривой в фазовой 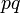 — плоскости за один период движения, равна целому числу умноженному на постоянную Планка
— плоскости за один период движения, равна целому числу умноженному на постоянную Планка 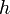 (Дебай, 1913 г.). С точки зрения рассмотрения постоянной тонкой структуры наиболее интересным является движение релятивистского электрона в поле ядра атома, когда его масса зависит от скорости движения. В этом случае мы имеем два квантовых условия:
(Дебай, 1913 г.). С точки зрения рассмотрения постоянной тонкой структуры наиболее интересным является движение релятивистского электрона в поле ядра атома, когда его масса зависит от скорости движения. В этом случае мы имеем два квантовых условия:
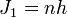 ,
, 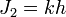 ,
,
где 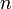 определяет главную полуось эллиптической орбиты электрона (
определяет главную полуось эллиптической орбиты электрона ( 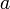 ), а
), а 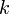 — его фокальный параметр
— его фокальный параметр 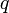 :
:
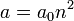 ,
, 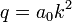 .
.
В этом случае Зоммерфельд получил выражение для энергии в виде
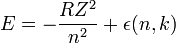 .
.
где 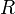 — постоянная Ридберга, а
— постоянная Ридберга, а 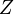 — порядковый номер атома (для водорода
— порядковый номер атома (для водорода 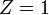 ).
).
Дополнительный член 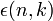 отражает более тонкие детали расщепления спектральных термов водородоподобных атомов, а их число определяется квантовым числом
отражает более тонкие детали расщепления спектральных термов водородоподобных атомов, а их число определяется квантовым числом 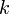 . Таким образом сами спектральные линии представляют собой системы более тонких линий, которые соответствуют переходам между уровнями высшего состояния (
. Таким образом сами спектральные линии представляют собой системы более тонких линий, которые соответствуют переходам между уровнями высшего состояния ( 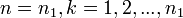 ) и низшего состояния (
) и низшего состояния ( 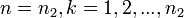 ). Это и есть т. н. тонкая структура спектральных линий. Зоммерфельд разработал теорию тонкой структуры для водородоподобных атомов (H,
). Это и есть т. н. тонкая структура спектральных линий. Зоммерфельд разработал теорию тонкой структуры для водородоподобных атомов (H, 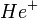 ,
, 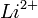 ), а Фаулер с Пашеном на примере спектра однократно ионизированного гелия
), а Фаулер с Пашеном на примере спектра однократно ионизированного гелия 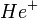 установили полное соответствие теории с экспериментом.
установили полное соответствие теории с экспериментом.
Зоммерфельд (1916 г.) еще задолго до возникновения квантовой механики Шредингера получил феноменологичную формулу для водородных термов в виде:
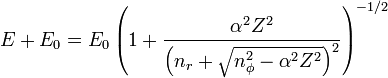 ,
,
где 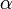 — постоянная тонкой структуры,
— постоянная тонкой структуры, 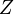 — порядковый номер атома,
— порядковый номер атома, 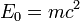 — энергия покоя,
— энергия покоя, 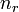 — радиальное квантовое число, а
— радиальное квантовое число, а 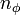 — азимутальное квантовое число. Позднее эту формулу получил Дирак используя релятивистское уравнения Шредингера. Поэтому сейчас эта формула и носит имя Зоммерфельда — Дирака.Появление тонкой структуры термов связана с прецессией электронов вокруг ядра атома. Поэтому появление тонкой структуры можно обнаружить по резонансному эффекту в области ультракоротких электромагнитных волн. В случае
— азимутальное квантовое число. Позднее эту формулу получил Дирак используя релятивистское уравнения Шредингера. Поэтому сейчас эта формула и носит имя Зоммерфельда — Дирака.Появление тонкой структуры термов связана с прецессией электронов вокруг ядра атома. Поэтому появление тонкой структуры можно обнаружить по резонансному эффекту в области ультракоротких электромагнитных волн. В случае 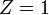 (атом водорода) величина расщепления близка к
(атом водорода) величина расщепления близка к
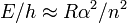
Поскольку длина электромагнитной волны равна
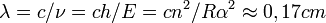
Поэтому для 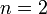 это будет почти 1 см.
это будет почти 1 см.
СВЕРХПРОВОДИМОСТЬ
Сверхпроводимость ¾ эффект скачкообразного падения сопротивления до нуля при T=Tk (критическая температура).
Сверхпроводимость открыта Киммерлинг-Оннесом в 1911 году, который наблюдал, что при Tk=4,2K электрическое сопротивление ртути скачкообразно падало до нуля.Сейчас известно ~ 1200 сверхпроводников.
МаксимальнуюTk=22,3K имеет сплав Na3Ge (1973 год).
Квантовая теория сверхпроводников создана в 1957 году Бардиным, Купером, Шриффером.
Резкий переход в сверхпроводящее состояние указывает на то, что все электроны проводимости одновременно во всём объёме металла переходят в новое состояние => должна быть корреляция состояний отдельных электронов. Физической причиной такой корреляции может быть взаимодействие электронов, но кулоновские силы приводят к отталкиванию. В данном же случае имеет место притяжение. Качественно механизм сверхпроводимости описывается через электронно-фононное взаимодействие. Это означает следующее: электроны, перемещаясь в решётке, деформируют её своим полем, т.е. смещают ионы из положения равновесия. Обратный переход ионов в исходное состояние сопровождается излучением энергии ¾ рождением фонона. Этот фонон поглощается другими электронами. В результате обмена фононами возникает связанное состояние электронов ¾куперовская пара. Минимальной энергией такая пара обладает, если импульсы взаимодействующих электронов равны по модули и противоположны по направлению, а спины ¾ антипараллельны.
Пара имеет спин = 0, т.е. она представляет собой бозе-частицу, которая не подчиняется принципу Паули. Они накапливаются в состоянии с минимальным значением энергии ¾бозе-конденсация.Куперовские пары, придя в согласованное движение, могут находиться в нём бесконечно долго сверхпроводимость.Участвовать в образовании куперовских пар могут лишь электроны, которые занимают энергетические уровни в слое;
При этом, если суммарная энергия двух электронов, находящихся на уровне Ферми, в нормальном состоянии = 2EF, то в состоянии сверхпроводимости энергия куперовской пары меньше и равна:
Куперовские пары при T=0 располагаются на уровне ниже уровня Ферми, который отделён от ближайшего уровня, отвечающего нормальному состоянию, наD.
При T=TkD=0 => сверхпроводимость исчезает.
Тепловое излучение
1. Излучательная и поглощательная способность тела. АЧТ. З-ны излучения.
Тепловое излучение: 0.2×10-7¾10-3 м (ультрафиолетовое, видимое, инфракрасное).
Есть два вида излучения телами электромагнитных волн:
Тепловое - э/м излучение испускается нагретыми телами или возникает за счёт внутренней энергии тела.
Люминесценция - излучение за счёт других видов энергии (хемлюминисценция, электралюминисценция, фотолюминесценция, катодолюминесценция).
Тепловое излучение имеет особенность-единственный вид излучения, которое может находиться в равновесии с излучающим телом, т.е. быть равновесным.
Энергия ТИ и его спектральный состав, т.е. зависимость энергии от частоты определяется температурой и природой тела.
Постоянство температуры нагретого тела можно обеспечить двумя способами: 1) притоком энергии извне; 2) поглощение телом энергии из окружающего пространства.
Если 2-й случай - тело находится в состоянии термодинамического равновесия, и спектральный состав зависит только от температуры.
Термодинамическое равновесие носит динамический характер.
Eпоглощения=Eизлучения- правило Прево
Источником равновесного излучения может служить замкнутая полость со стенками не проводящими тепла и поддерживаемая при постоянной температуре.
1.2 Характеристики теплового излучения {к: 3-5}
1) Спектральная испускательная способность (испуск. способность):
СИС ¾ энергия, испускаемая в единицу времени единичной площадкой в единичном интервале частот: r(w,T)=dE/(dtdSsw)
2) Интегральная испускательная способность (аналитическая светимость):
ИИС ¾ поток энергии, испускаемый единичной площадкой во всех направлениях в пределах < 2p : R(T)=or(w,T)dw {0, ?}
Излучение может характеризоваться как w так и l. Участку спектра dw соответствует dl: w=(2pc)/l ;dw=[(-2pc)/l2]dl
Если dw и dl соответствуют одному и тому же участку спектра, то выполняется соотношение: r(w, T)dw = r ’(l,T)dl
Т.о.: r(w, T)=r’(l,T)?(l2/2pc)
3) Поглощательная способность:
ПС ? отношение потока энергии, поглощаемого элементарной площадкой к падающему на неё потоку: a(w, T)=dФ’/dФ
dФw- поток, заключённый в dw ; a(w, T)?1
Тело, полностью поглощающее все падающие на него потоки ? Абсолютно Чёрное Тело (АЧТ) (a=1)
Существует максимально возможное количество энергии, испускаемое при данной температуре. Источник -АЧТ.
АЧТ в природе не существует.
Устройством, моделирующим АЧТ, является вогнутая полость с отверстием и непроницаемыми стенками с некоторой постоянной температурой.
Излучение АЧТ - равновесное.
2. Закон Стефана-Больцмана. Вина.
Попытки найти аналитический вид f(  ,T) или U(
,T) или U(  ,T) привели к установлению рада законов теплового излучения:
,T) привели к установлению рада законов теплового излучения:
Закон Стефана-Больцмана .На основе экспериментальных данных Стефан ошибочно предположил, что R ~ T4 (в 1879).В 1884 Больцман выяснил, что это справедливо только для АЧТ.
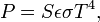
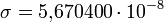 Дж·с−1·м−2 · К−4.
Дж·с−1·м−2 · К−4.
Закон смещения Вина
На основе т/д соображений и э/м теории немецкий физик Вин в 1893 году нашёл общий вид функции распределения энергии по частотам в спектре излучения АЧТ: f(  ,T)= λ 3F(λ,T);
,T)= λ 3F(λ,T);
j( λ,T)=[(2пc)/ λ]3×F[(2пc)/  T] × [(2пc)/ λ 2] Как следует из приведённых выражений, при изменении температуры вид f(λ, T) и j( λ, T) сохраняется в смещённой шкале частот.
T] × [(2пc)/ λ 2] Как следует из приведённых выражений, при изменении температуры вид f(λ, T) и j( λ, T) сохраняется в смещённой шкале частот.
Отсюда следует название закона.
Положение максимума этих функций удовлетворяет условию:
λmax/T=const ;
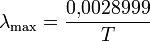
закон смещения Вина; м\к ¾ постоянная Вина.Закон Рэлея-Джинса
Для получения явного вида 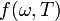 необходимо обратиться к конкретной модели излучения.С точки зрения классической теории АЧТ можно представить как совокупность осцилляторов, совокупная энергия которых ~ квадрату амплитуды колебаний и непрерывно меняется.Равновесное излучение в полости можно представить как совокупность стоячих волн различных частот, количество которых в единице объёма:
необходимо обратиться к конкретной модели излучения.С точки зрения классической теории АЧТ можно представить как совокупность осцилляторов, совокупная энергия которых ~ квадрату амплитуды колебаний и непрерывно меняется.Равновесное излучение в полости можно представить как совокупность стоячих волн различных частот, количество которых в единице объёма:
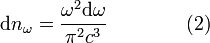
Рэлей и Джинс попытались установить аналитический вид f(  ,T), опираясь на
,T), опираясь на 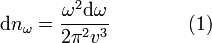
и исходя из теоремы равномерном распределении энергии по степеням свободы.
Они предположили, что на каждую стоячую волну в среднем приходится энергия 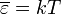 (по 1/2 на электрическую и магнитную составляющие).
(по 1/2 на электрическую и магнитную составляющие). 
Отсюда следует вид U(  ,T):
,T):
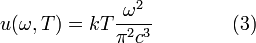
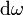 интервал частот
интервал частот
Вывод формулы Рэлея-Джинса безупречен с классической позиции, но он удовлетворяет экспериментальным данным только на малых частотах.
Закон Рэлея-Джинса
Для получения явного вида 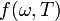 необходимо обратиться к конкретной модели излучения.
необходимо обратиться к конкретной модели излучения.
С точки зрения классической теории АЧТ можно представить как совокупность осцилляторов, совокупная энергия которых ~ квадрату амплитуды колебаний и непрерывно меняется.
Равновесное излучение в полости можно представить как совокупность стоячих волн различных частот, количество которых в единице объёма:
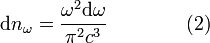
Рэлей и Джинс попытались установить аналитический вид f(  ,T), опираясь на
,T), опираясь на 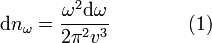
и исходя из теоремы равномерном распределении энергии по степеням свободы.
Они предположили, что на каждую стоячую волну в среднем приходится энергия 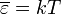 (по 1/2 на электрическую и магнитную составляющие).
(по 1/2 на электрическую и магнитную составляющие).  Отсюда следует вид U(
Отсюда следует вид U(  ,T):
,T):
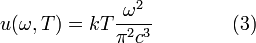
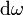 интервал частот
интервал частот
Вывод формулы Рэлея-Джинса безупречен с классической позиции, но он удовлетворяет экспериментальным данным только на малых частотах
ФОРМУЛА ПЛАНКА
В 1900 году Планку удалось отыскать вид f(  ,T), который удовлетворял опыту во всех диапазонах частот.
,T), который удовлетворял опыту во всех диапазонах частот.
Была выдвинута гипотеза, что энергия испускается в виде отдельных порций, величина которых ~ h  =
= 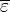 ;
;
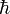 = 1.054 · 10−27эрг·с.Размерностьh совпадает с “размерностью действия” (энергия × время) => постоянная Планка называется квантом действия.
= 1.054 · 10−27эрг·с.Размерностьh совпадает с “размерностью действия” (энергия × время) => постоянная Планка называется квантом действия.
Из постулатов Планка следует, что если э/м излучение испускается порциями h  , то его энергия кратна этой величине.
, то его энергия кратна этой величине.
Математически это означает дискретность => нужно применять суммирование, а не интегрирование.
< 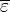 >=ЕnPn, Pn¾ вероятность того, что Е колебания с
>=ЕnPn, Pn¾ вероятность того, что Е колебания с  имеет значение Еn ;
имеет значение Еn ;
В состоянии равновесия распределение колебаний по значениям энергии подчиняется закону Больцмана:
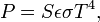
Среднее значение энергии колебаний частоты  равно:
равно:
; 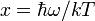 Допустим, что
Допустим, что  (и x) изменяется непрерывно:
(и x) изменяется непрерывно:
средняя 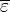 , приходящаяся на степень свободы, не одинакова для разных частот стоячих волн.
, приходящаяся на степень свободы, не одинакова для разных частот стоячих волн.
< 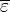 >=kT;
>=kT;
С ростом  средняя Е убывает => интеграл светимости сходится.
средняя Е убывает => интеграл светимости сходится.
U(  , T)d
, T)d  =<Е>/[
=<Е>/[  2/(п2c3)]d
2/(п2c3)]d 
Из формулы Планка следует:
1) Закон Рэлея-Джинса ( 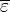
 <<kT):...
<<kT):...
f(  , T)=[
, T)=[  2/(4п2c2)]\kT;
2/(4п2c2)]\kT;
2) Закон излучения Вина ( 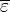
 >>kT):
>>kT):
f(  , T)=[(
, T)=[( 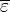
 3)/(4п2c2)]e-hw/kT);
3)/(4п2c2)]e-hw/kT);
3) Закон Стефана-Больцмана:
4) 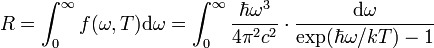 Закон смещения Вина:
Закон смещения Вина:
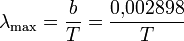
Таким образом формула Планка описывает все свойства равновесного теплового излучения.
5.Фотоэффе́кт — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
ЗАКОНЫ ФОТОЭФФЕКТА
1) При неизменном спектральном составе света сила тока насыщения пропорциональна падающему световому потоку: Iн ~ Ф
2) Начальная кинетическая энергия линейно растёт с увеличением частоты и не зависит от интенсивности: m  2max/2=
2max/2= 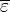 Uз ;
Uз ;
3) Существует минимальная частота (  minили λmax), характерная для каждого металла, начиная с которой фотоэффект не происходит.
minили λmax), характерная для каждого металла, начиная с которой фотоэффект не происходит.
 min¾ красная граница
min¾ красная граница
6. Внешний фотоэффект по Энштейну. Установленные экспериментально зависимости не могли быть объяснены. Все особенности фотоэффекта объяснил в 1905м году Эйнштейн ¾ “свет поглощается тоже квантами”.
Используя гипотезу квантов, он вывел формулу: 
 =Aвых + Ekmax
=Aвых + Ekmax
Ekmax = m  2max/2 ,
2max/2 ,  << c ; Ek = E-E0 ,
<< c ; Ek = E-E0 ,  ~ c
~ c
Ekmax = Ekmax (  );y=kx-b;
);y=kx-b;
Мы рассматриваем однофотонный фотоэффект при малых световых потоках: квант поглощается одним электроном.
Мощные лазеры дают многофотонный фотоэффект.
В полупроводниках и диэлектриках имеет место внутренний фотоэффект.
Для объяснения законов теплового излучения Планк предположил, что электромагнитное излучение испускается квантами. Для объяснения фотоэффекта Эйнштейн предположил поглощение квантами.Он же предположил, что электромагнитное излучение распространяется квантами => оно ¾ совокупность фотонов, а классическое представление об электромагнитном поле оказывается верным лишь для предельного случая (число фотонов велико).
Подтверждающий эксперимент ¾ опыт Ботэ.
Слабое рентгеновское излучение падает на фольгу, которая становится источником вторичного излучения (флуоресценция), которое попадает на счётчик => отметка на ленте.
Если бы излучаемая энергия распределялась равномерно, то отметки на ленте были бы симметричны. Беспорядок отметок => дискретные частицы (фотоны).
Точная теория электромагнитного поля, как поля квантованного, ¾ называется квантовой электродинамикой, согласно которой движение фотонов не может быть описано без учёта волновых свойств.Соотношения между волновыми и корпускулярными свойствами можно выяснить по распределению интенсивности освещения экрана.
I ~ A2 (волновое представление)
Согласно корпускулярному представлению ¾I ~ плотности потока фотона.Количество фотонов, регистрируемое фотоумножителем, ¾ случайное в данной точке => вероятность обнаружения фотона в пределах dV определяется выражением: dP=cA2dV, c¾ коэффициент пропорциональности
Эффект Комптона
1923 ¾ рассеивающее вещество в рентгеновском излучении содержит кроме исходного (с λ) излучение и с большей λ’ ,
причём D λ = λ’- λ = λc(1-cos α) ¾ зависит только от угла α между начальным пучком и направлением рассеивания и не зависит от λ и типа вещес<
