Дифракция электронов. Гипотеза Луи де Бройля.

Он постулировал универсальность корпускулярно волнового дуализма, т.е. все положения дуализма могут быть применимы ко всем частицам материи.

Это означает для каждой частицы материи можно ввести поннятия:

E = hn = hc/n сл-но можнл вычислит l.

Импульс P = h/l = ħk; ħ – волновое число ħ = р/2p; l_D = h/P = h/m₀n - длинна волны де Бройля.

Экспериментальное подтверждение гипотезы Луи де Бройля.

В эксперименте по рассеянию электронов на кристаллах и по прохождению этих частиц через вещество; если электрон рассеивается на кристалле.

По де Бройлю частица обладает волновыми свойствами сл-но с этой частицей связываем плоскую монохроматическую волну.

y(^®r,t)=Aexp(–I(wt - kr)) – плоская монохроматическая волна.

Сделаем замену переменной в экспаненте и перейдем от w к энергии, через e = hc/p от k перейти к импульсу:

y(^®r,t)=Aexp(-i/ħ (Et –®p®r)) – плоская волна де Бройля.

Соотношения неопределённостей.

Соотношения неопределённостей – фундаментальные соотношения квантовой механики, устанавливающие предел точности одновременного определения так называемых дополнительных физических величин, характеризующих систему (например, координаты и импульса). В упрощённой формулировке эти соотношения утверждают, что дополнительные физические величины не могут быть одновременно точно определены. Неопределённостей соотношения являются следствием двойственной, корпускулярно-волновой природы частиц материи, отражением вероятностной (статистической) сути квантовой механики.

Неопределённостей соотношения имеют вид неравенств, например, xp > = h/2, где x – неопределённость координаты (частицы или системы), p – неопределённость её импульса, а h = 6.6.10-34 Дж.с = 4.1.10-15 эВ.с - постоянная Планка. Отсюда видно, что произведение неопределённостей координаты и импульса не может быть меньше , и никаким усовершенствованием методов наблюдения нельзя преодолеть этот рубеж. Увеличение точности определения координаты неизбежно ведёт к потере точности определения импульса. Предельная точность одновременного определения координаты и импульса даётся соотношением x·p.

Уравнение Шредингера.

Квантовая механика способна объяснить поведение микрочастиц. Подобно тому, как законы Ньютона не выводятся, а является обобщением большого числа опытных фактов, так и уравнение Шредингера не выводятся. Оно постулируется. Шредингер записал уравнение, основываясь на экспериментальных результатах.

Состояние микрочастиц в квантовой механике описывается волновой функцией 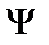. Она является функцией координат и времени и может быть найдена из уравнения Шредингера:

.

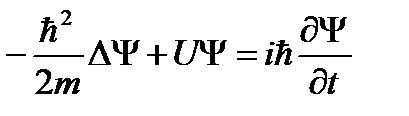Это временное уравнение Шредингера для случая, когда 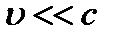. Здесь i - мнимая единица ( 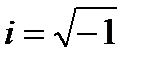), , 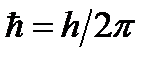m - масса частицы, - оператор Лапласа ( 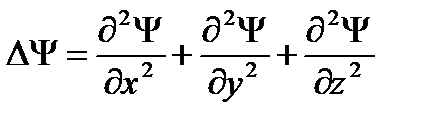), 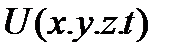- потенциальная энергия частицы.