Основные законы и формулы раздела “Волновая и квантовая оптика”.

•Скорость света в среде:

,

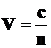где 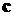– скорость света в вакууме; 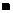– показатель преломления среды.

•Оптическая длина пути света в среде:

,

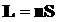где 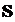– геометрическая длина пути в среде с показателем преломления n.

•Оптическая разность хода двух световых волн:

.

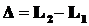•Разность фаз двух волн:

,

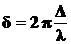где 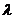– длина световой волны в вакууме.

•Условие максимального усиления света при интерференции (условие максимума):

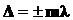или ,

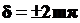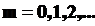
•Условие наибольшего ослабления света (условие минимума):

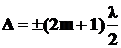или ,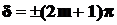

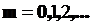
•Оптическая разность хода лучей, возникающая при прохождении и отражении монохроматического света от тонкой пленки, расположенной в воздухе, без учета дополнительной разности хода, возникающей при отражении от среды оптически более плотной:

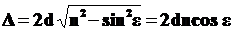
где 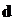– толщина пленки; 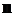– показатель преломления пленки; 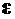– угол падения луча на пленку, 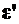– угол преломления света в пленке.

При каждом отражении от среды оптически более плотной к оптической разности хода добавляется .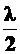

•Радиус светлых колец Ньютона в отраженном свете:

,

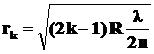где 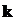– номер кольца ; 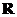– радиус кривизны линзы, 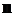- показатель преломления жидкости, налитой между линзой и плоскопараллельной пластинкой.

•Радиус темных колец Ньютона в отраженном свете:

.

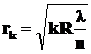
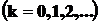При наблюдении колец Ньютона в проходящем свете вышеприведенные формулы для радиусов светлых и темных колец меняются местами.

•Расстояние между интерференционными полосами на экране, которые получаются в результате сложения волн от когерентных источников:

,

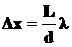где 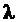– длина волны света; 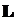– расстояние от экрана до источников света, отстоящих друг от друга на расстояние .

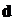•Радиус 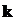-й зоны Френеля для сферической волны:

,

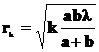где 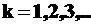, 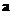– расстояние от источника волн до волновой поверхности и 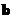– расстояние от волновой поверхности до точки наблюдения.

•Радиус 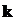-й зоны Френеля для плоской волны:

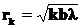
•Положение минимумов (темная полоса) освещенности при дифракции от щели, на которую нормально падает пучок параллельных лучей, определяется условиями:

, ,

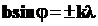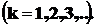где 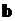– ширина щели; 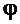– угол дифракции; 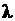– длина волны падающего света.

•Положение главных максимумов при дифракции на решетке, на которую нормально падает пучок параллельных лучей, определяется условием:

, ,

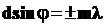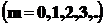где 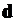– период дифракционной решетки; 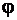– угол дифракции, - номер максимума для монохроматического света (порядок спектра для белого света).

•Разрешающая способность дифракционной решетки:

,

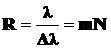где 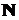– общее число щелей решетки; и 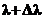– длины волн двух близких спектральных линий, которые в 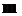порядке видны как раздельные.

•Закон Брюстера:

,

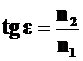где 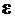– угол падения луча, при котором отразившийся от диэлектрика луч полностью поляризован; 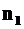– показатель преломления первой среды, 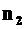– показатель преломления второй среды.

•Закон Малюса:

,

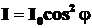где 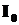– интенсивность плоскополяризованного света, падающего на поляризатор; 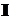– интенсивность света, вышедшего из поляризатора, – угол между плоскостью колебаний вектора 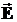в падающей волне и плоскостью колебаний вектора 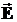в вышедшей волне.

•Закон Малюса с учетом потерь на отражение и поглощение в поляризаторе:

,

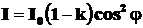где – коэффициент потерь на отражение и поглощение в поляризаторе; 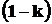– коэффициент пропускания.

•Энергетическая светимость:

,

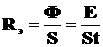где 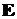– энергия, излучаемая поверхностью, площадь которой 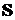, 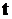– время излучения, 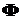– поток излучения.

•Закон Стефана-Больцмана:

,

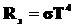где 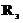– энергетическая светимость черного тела, 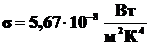– постоянная Стефана-Больцмана, 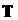– термодинамическая температура по шкале Кельвина.

•Энергетическая светимость серого тела:

,

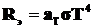где 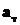– поглощательная способность серого тела/

•Закон смещения Вина:

,

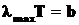где 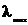– длина волны, на которую приходится максимум спектральной плотности энергетической светимости; 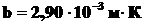– постоянная Вина.

•Энергия фотона:

,

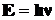где 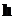– постоянная Планка; 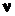– частота.

•Импульс фотона:

.

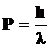•Формула Эйнштейна для фотоэффекта:

,

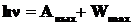где – энергия фотона, падающего на поверхность металла; – работа выхода электрона из металла; 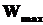– максимальная кинетическая энергия фотоэлектрона.

•Красная граница фотоэффекта:

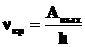
•Задерживающее напряжение:

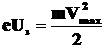
•Формула Комптона:

,

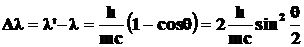где 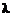– длина волны падающего фотона; 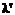– длина волны фотона, рассеянного на угол 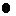после столкновения; – масса частицы, на которой происходит рассеяние.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. От двух когерентных источников О₁ и О₂ (λ = 600нм) лучи падают на экран. На экране наблюдается интерференционная картина. Когда на пути одного из лучей перпендикулярно ему поместили тонкую стеклянную пластинку, показатель преломления которой n = 1,5, то центральная светлая полоса сместилась в положение, первоначально занятое пятой светлой полосой. При какой толщине d пластинки это возможно?

Решение

В результате внесения стеклянной пластинки разность хода между интерферирующими лучами изменится. Первоначальная разность хода равна , после внесения пластинки: . Так как произошло смещение на полос, то добавочная разность хода . Следовательно, . Откуда . После подстановки числовых значений величин найдем:

Пример 2.На стеклянный клин (n_ст = 1,5) с малым углом нормально к его грани падает параллельный пучок лучей монохроматического света с длиной волны l = 0,6 мкм. Число m возникающих при этом интерференционных полос, приходящихся на 1 см, равно 10. Наблюдение ведется в отраженном свете. Определить угол a клина.

Решение

Интерферировать будут волны 1 и 2,отраженные соответственно от верхней и нижней грани клина. Интерференционная картина наблюдается вблизи поверхности клина.

Пусть произвольной темной интерференционной полосе k-ого номера соответствует толщина b_k клина, а темной интерференционной полосе k+m-ого номера—толщина b_k+m клина. Разность хода D двух волн, образующих интерференционную полосу, складывается из разности оптических длин путей этих волн и добавочной разности хода , которая возникает при отражении волны 1 от оптически более плотной среды.

Темные полосы видны на тех участках клина, для которых разность хода волн удовлетворяет условию минимума, т. е.:

После упрощения получим для k-той полосы

Соответственно для k+m-ой полосы

Из рисунка видно, что

Выразив из предыдущих равенств и , получим:

Учитывая, что угол мал , получим:

Подставляя числовые значения физических величин, найдем

.

Пример 3. На дифракционную решетку нормально падает параллельный пучок лучей с длиной волны λ = 500 нм. На экране, параллельном дифракционной решетке и отстоящем от нее на расстояние L = 1 м, получается дифракционная картина. Расстояние между максимумами первого порядка, наблюдаемыми на экране, равно =20,2 см. Определить: 1) постоянную дифракционной решетки; 2) число максимумов, даваемых дифракционной решеткой; 3) максимальный угол отклонения лучей.

Решение

Воспользуемся формулой, определяющей положение максимумов при дифракции на решетке: , где – порядок спектра. Из рисунка видно, что . Обычно угол дифракции ( =1) первого порядка мал и можно считать

, тогда .

Подставив численные значения, имеем:

Для определения числа максимумов, даваемых дифракционной решеткой, вычислим максимальный порядок спектра m_max, который определяется из условия, что максимальный угол отклонения лучей дифракционной решеткой не может превышать 90^о, т.е. . Тогда для получим:

Так как – обязательно целое число, то (округлять до 10 нельзя, т.к. тогда ).

Итак, влево и вправо от центрального (нулевого) максимума будет наблюдаться одинаковое число максимумов, равное , учитывая также центральный максимум, получаем:

.

Максимальный угол отклонения лучей, соответствующих последнему дифракционному максимуму, найдем по формуле

,

т.е.

Откуда искомое значение угла

.

Пример 4. Естественный свет проходит через поляризатор и анализатор, установленные так, что угол между их плоскостями пропускания равен φ. Как поляризатор, так и анализатор поглощают и отражают 8% падающего на них света. Оказалось, что луч, вышедший из анализатора, имеет 9% от интенсивности естественного света, падающего на поляризатор. Найти угол φ.

Решение. Интенсивность естественного света, прошедшего через поляризатор, по закону Малюса равна:

,

где – коэффициент потерь интенсивности света в поляризаторе; коэффициент 1/2 появляется при усреднении по всем состояниям поляризации падающего света.

Интенсивность света, прошедшего через анализатор, определяется также по закону Малюса:

.

Где – интенсивность света, падающего на анализатор; – угол между плоскостями пропускания поляризатора и анализатора; – коэффициент потерь интенсивности света в анализаторе.

Подставим из первой формулы и учтем, что вышедший из анализатора свет составляет 9% от интенсивности естественного света:

По условию задачи = = 0,08. Сокращая на , получим:

Искомое значение угла

.

Пример 5. Определить максимальную скорость фотоэлектронов, вырываемых с поверхности серебра ультрафиолетовыми лучами с длиной волны λ = 0,160 мкм.

Решение. Максимальную скорость фотоэлектронов можно найти из уравнения Эйнштейна для фотоэффекта:

,

где – энергия фотонов, падающих на поверхность металла; – работа выхода электрона из металла; – максимальная кинетическая энергия фотоэлектронов.

Энергию фотона можно выразить через длину волны :

.

Кинетическая энергия электрона может быть определена по классической формуле:

,

Подставим энергию фотона и кинетическую энергию в уравнение Эйнштейна:

,

откуда

Используя значение (из таблиц), получаем

.

Пример 6. В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол . Энергия рассеянного фотона . Определить энергию фотона до рассеяния.

Решение. Для определения энергии первичного фотона воспользуемся формулой Комптона:

,

где – изменение длины волны фотона в результате рассеяния на свободном электроне; Θ – угол рассеяния фотона.

Выразим длины волн и через энергии и фотонов:

.

Умножая числитель и знаменатель правой части формулы Комптона на скорость фотона c, получаем:

Сократим на и найдем :

Вычисления по этой формуле удобно вести во внесистемных единицах, где энергия покоя электрона :

Пример 7.В результате эффекта Комптона фотон с энергией 0,51 МэВ был рассеян на свободном электроне на угол . Определить угол рассеяния электрона.

Решение: Энергия фотона 0,51 МэВ соответствует энергии покоя электрона mс². Длина волны фотона с такой энергией равна =2,43 пм, что соответствует комптоновской длине волны . Рассчитаем по формуле Комптона длину волны рассеянного фотона: Так как , получаем . Из закона сохранения импульса для проекции на ось X: следует: . Подставив найденные величины, получим: . Упростив, получим: .

Импульс электрона можно определить из известной релятивистской формулы: . Кинетическую энергию электрона найдем из закона сохранения энергии: . Подставим найденное соотношение в предыдущую формулу: .

Упрощая, получим: . Тогда, использовав эту формулу, будем иметь: следовательно, . Искомый угол равен .

Пример 8. Длина волны, на которую приходится максимум энергии в спектре излучения черного тела, равна λ_max = 0,58 мкм. Определить энергетическую светимость поверхности тела.

Решение. Энергетическая светимость черного тела может быть найдена из закона Стефана-Больцмана:

Температуру найдем из закона смещения Вина:

.

Отсюда:

.

Контрольная работа № 5

Указания к выполнению и оформлению контрольной работы.

К решению задач следует приступать после тщательного изучения теории соответствующего раздела. Каждая задача должна быть оформлена на отдельном листе с указанием фамилии студента, группы, номера варианта и дня сдачи. Условие задачи нужно переписывать полностью. Решение задачи должно сопровождаться подробными пояснениями. Работы, содержащие в решении только набор формул, к проверке не принимаются. Как правило, необходимо делать чертеж (р[1]исунок), поясняющий решение задачи. Решение задачи желательно получить в общем виде, а затем подставить числовые значения заданных величин, выраженных в единицах системы СИ.

Номер варианта соответствует порядковому номеру фамилии студента в журнале группы.

№ номер в журнале группы	Н о м е р а з а д а ч

Интерференция света

В задачах данного раздела обязателен рисунок, показывающий ход лучей и область интерференции.

501. Сферическая поверхность плосковыпуклой линзы (n₁ = 1,52) соприкасается со стеклянной пластинкой (n₂ = 1,7). Пространство между линзой, радиус кривизны которой R = 1,0 м, и пластинкой заполнено жидкостью. Наблюдая кольца Ньютона в отраженном свете (λ = 0,589 мкм), измерили радиус десятого темного кольца r₁₀ = 2,05 мм. Определить показатель преломления жидкости n_ж, если n_ж<n₁<n₂.

502. Для уменьшения потерь света при отражении от стекла на поверхность объектива (n₂ = 1,7) нанесена прозрачная пленка (n = 1,3). При какой наименьшей толщине ее произойдет максимальное ослабление отраженного света, длина волны которого приходится на среднюю часть видимого спектра (λ = 0,56 мкм)? Считать, что лучи падают нормально к поверхности объектива.

503. Между двумя плоскопараллельными стеклянными пластинками заключен очень тонкий воздушный клин. На пластинки нормально падает монохроматический свет (λ = 0,50 мкм). Определить угол α между пластинками, если в отраженном свете на протяжении l = 1см наблюдается N = 20 интерференционных полос.

504. Сферическая поверхность плосковыпуклой линзы (n₁ = 1,52) соприкасается со стеклянной пластинкой (n₂ = 1,7). Пространство между линзой, радиус кривизны которой R = 1,0 м, и пластинкой заполнено жидкостью. Наблюдая кольца Ньютона в отраженном свете (λ = 0,608 мкм), измерили радиус десятого темного кольца r₁₀ = 1,90 мм. Определить показатель преломления жидкости n_ж, если n₁<n_ж<n₂.

505. Плоскопараллельная пластинка с показателем преломления n = 1,50 освещается параллельным пучком монохроматического света (λ = 0,59 мкм). При постепенном увеличении угла падения лучей ε интерференционная картина в отраженном свете изменяется. Определить толщину пластинки b, зная, что при измерении угла ε в некотором интервале имеются лишь два значения ε₁ = 30° и ε₂ = 34°, соответствующие максимальной интенсивности отраженного света.

506. Между двумя плоскопараллельными стеклянными пластинками (n_ст = 1,5) заключен очень тонкий клин, заполненный жидкостью (n_ж = 1,7). Угол клина равен 30¢¢. На пластинки нормально падает монохроматический свет с длиной волны λ = 0,55 мкм. Определить, какое число светлых интерференционных полос наблюдается на протяжении 1см, если наблюдение проводится в отраженном свете.

507. Свет с длиной волны λ = 0,55 мкм падает на поверхность стеклянного клина под углом ε = 15°. Показатель преломления стекла n = 1,5, угол при вершине клина α = 1¢. Определить расстояние между двумя соседними минимумами при наблюдении интерференции в отраженном свете.

508. Какого цвета будет мыльная пленка в отраженном и проходящем свете, если на нее падает белый свет под углом 45°? Толщина пленки 0,45 мкм, показатель преломления равен 1,33.

509. На тонкий стеклянный клин падает нормально монохроматический свет с длиной волны 600нм. Расстояние между соседними интерференционными полосами в отраженном свете L = 0,4 мм, показатель преломления стекла n_cn = 1,5. Определить угол между поверхностями клина.

510. В установке для наблюдения колец Ньютона пространство между стеклянной линзой и стеклянной пластинкой заполнено жидкостью (n_ж<n_ст). Определить показатель преломления жидкости, если радиус третьего светлого кольца получился равным 3,65 мм. Наблюдение ведется в проходящем свете. Радиус кривизны линзы 10 м. Длина волны света 5,89∙10^-5 см.

511. Плосковыпуклая линза положена на стеклянную пластинку выпуклой стороной и освещается монохроматическим светом с длиной волны 600 нм. Найти радиус кривизны линзы, если радиус седьмого темного кольца Ньютона в отраженном свете равен 2,2 мм.

512. Расстояние между пятым и двадцать пятым светлыми кольцами Ньютона равно 9 мм. Радиус кривизны линзы равен 15 м. Найти длину волны монохроматического света, падающего нормально на установку. Наблюдение проводится в отраженном свете.

513. Установка для наблюдения колец Ньютона освещается монохроматическим светом с длиной волны 589 нм, падающим нормально. Определить толщину воздушного слоя между линзой и стеклянной пластинкой в том месте, где наблюдается шестое темное кольцо в отраженном свете.

514. Плосковыпуклая стеклянная линза с радиусом кривизны 1 м положена на стеклянную пластинку выпуклой стороной. Радиус пятого светлого кольца Ньютона в проходящем свете равен 1,5 мм. Найти длину волны монохроматического света, падающего нормально на установку, если пространство между линзой и пластинкой заполнено жидкостью с показателем преломления n_ж = 1,33. Показатель преломления стекла n_ст = 1,5.

515. В установке для наблюдения колец Ньютона пространство между линзой с радиусом кривизны 5 м и стеклянной пластинкой заполнено жидкостью с показателем преломления n_ж = 1,33. Определить радиус третьего светлого кольца Ньютона в проходящем свете. Длина волны света равна 600 нм. Свет падает нормально к поверхности линзы.

Дифракция света

В задачах данного раздела обязателен рисунок, показывающий ход лучей

516. На диафрагму с круглым отверстием падает нормально параллельный пучок монохроматического света (λ = 600 нм). На экране наблюдается дифракционная картина. При каком наибольшем расстоянии между диафрагмой и экраном в центре дифракционной картины еще будет наблюдаться минимум освещенности? Диаметр отверстия 1,96 мм.

517. На какую длину волны в спектре второго порядка накладывается фиолетовая линия (λ = 0,4 мкм) спектра третьего порядка, если на дифракционную решетку падает нормально параллельный пучок белого света?

518. На дифракционную решетку, содержащую 500 штрихов на миллиметр, падает нормально белый свет. Определить длину спектра первого порядка на экране, если расстояние от решетки до экрана 1м. Границы видимого спектра: λ_кр= 780нм, λ_ф = 400 нм.

519. На дифракционную решетку, имеющую 5000 штрихов на 1 см, падает нормально параллельный пучок белого света. Найти разность углов отклонения конца первого и начала второго порядков спектра. Длины красных и фиолетовых волн принять равными 760нм и 400нм.

520. Дифракционная картина наблюдается на расстоянии X от точечного источника монохроматического света (λ = 600 нм). На расстоянии 0,3∙X от источника помещена круглая непрозрачная преграда диаметром 1 мм. Чему равно расстояние X, если преграда закрывает только центральную зону Френеля?

521. Найти наибольший порядок спектра для линий с длинами волн 400нм и 600 нм, если постоянная дифракционной решетки равна 5 мкм. Сколько штрихов на 1 см имеет такая решетка?

522. Между точечным источником света и экраном поместили диафрагму с круглым отверстием, радиус r которого можно менять. Расстояния от диафрагмы до источника и экрана равны a = 100 см и b = 125 см. Определить длину волны света, если максимум освещенности в центре дифракционной картины на экране наблюдается при r₁ = 1,0 мм и следующий при r₂ = 1,29 мм.

523. На круглое отверстие диаметром d = 4мм падает нормально параллельный пучок лучей (λ = 0,5 мкм). Точка наблюдения находится на оси отверстия на расстоянии b = 2м от него. Сколько зон Френеля укладывается в отверстии? Минимальная или максимальная освещенность пятна получится в центре дифракционной картины, если в месте наблюдения поместить экран?

524. Период дифракционной решетки d = 0,01 мм. Какое наименьшее число штрихов должна содержать решетка, чтобы две составляющие желтой линии натрия (λ₁ = 589,0 нм, λ₂ = 589,6 нм) можно было видеть раздельно в спектре первого порядка? Определить наименьшую длину L решетки

525. Длина решетки L = 15 мм, период d = 5 мкм. В спектре какого наименьшего порядка получаются раздельные изображения двух спектральных линий с разностью длин волн ∆ λ = 0,1 нм, если линии лежат в крайней красной части спектра (от 780 до 700 нм)?

526. Сколько порядков спектров для линий с длинами волн 400 нм и 600 нм можно наблюдать от дифракционной решетки, имеющей 500 штрихов на 1 мм? Найти максимальные углы отклонения этих спектральных линий.

527. На дифракционную решетку, имеющую 5000 штрихов на 1 см, падает нормально белый свет. Спектр проектируется на экран линзой, помещенной вблизи решетки. Определить ширину спектра второго порядка на экране, если расстояние от линзы до экрана 0,5 м. Границы видимого спектра: l_кр = 750 нм и l_ф = 400 нм.

528. Длина дифракционной решетки L = 16 мм и период d = 4 мкм. В спектре какого наименьшего порядка получаются раздельные изображения двух спектральных линий с разностью длин волн Dl = 0,1 нм, если линии лежат в области 400 нм? Найти угол отклонения спектральной линии (l = 750 нм) в этом порядке.

529. На непрозрачную преграду с отверстием диаметром d = 2 мм падает монохроматическая плоская световая волна. Когда расстояние от преграды до экрана равно b₁ = 57,5 см, в центре дифракционной картины наблюдается максимум интенсивности. При увеличении расстояния до b₂ = 86,2 см максимум интенсивности сменяется минимумом. Определить длину волны света.

530. На препятствие с круглым отверстием диаметром 1мм падает плоская монохроматическая волна l=600нм. С какого минимального расстояния между отверстием и экраном в центре дифракционной картины будет наблюдаться только максимум освещенности?

Поляризация света

531. Угол полной поляризации для некоторого вещества равен 56°. Чему равен предельный угол полного отражения для этого вещества?

532. Естественный свет падает на систему из трех последовательно расположенных одинаковых поляроидов, причем плоскость пропускания среднего поляроида составляет угол φ = 60° с плоскостями пропускания двух других поляроидов. Каждый поляроид обладает коэффициентом пропускания τ = 0,81. Во сколько раз уменьшится интенсивность света после прохождения этой системы?

533. Интенсивность луча, вышедшего из анализатора, равна 10% интенсивности естественного света, падающего на поляризатор. Найти угол между плоскостями пропускания поляризатора и анализатора, если каждый из них поглощает и отражает 5% падающего на них света.

534. Во сколько раз уменьшится интенсивность естественного света после прохождения двух николей, каждый из которых поглощает 10% падающего на него света, если угол между их плоскостями пропускания 60°?

535. На какой угловой высоте над горизонтом должно находиться Солнце, чтобы солнечный свет, отраженный от поверхности воды, был полностью поляризован? n_воды = 1,33

536. Луч света, идущий в воде, отражается от грани алмаза, погруженного в воду. При каком угле падения отраженный луч полностью поляризован? n_воды = 1,33, n_алм = 2,42

537. Угол полной поляризации при отражении света от кристалла каменной соли 57°. Определить скорость распространения света в этом кристалле

538. Предельный угол полного отражения для некоторого вещества равен 45°. Чему равен для этого вещества угол полной поляризации отраженного луча?

539. Чему равен угол м