Потенциальная энергия во внешнем поле сил

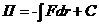, С – постоянная интегрирования.

Связь силы с потенциальной энергией

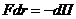
№14

Закон сохранения инергии

Рассмотрим систему мат. точек с массами 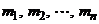со скоростями 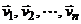. Пусть 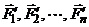– равнодействующие внутренних консерв. сил, действующих на точки, а 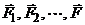– равнодействующая внешних консерв. сил. Равнодействующие внешних неконсерв. сил: .

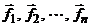По второму ур. Ньютона:

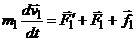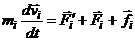, => . Умножим каждое из ур. скалярно на соответствующее перемещение, учитывая, что 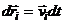и просуммируем:

;

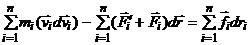Первый член равен: ;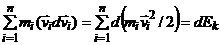

Второй член равен: ,.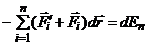

Правая часть задает работу внешних консервативных сил. Получаем: .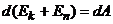

Если внешние неконсерв. силы отсутствуют, то получим: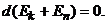

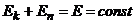, т. е. полная мех. энергия системы сохраняется постоянной.

№15

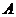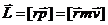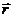Моментом импульсаматериальной точки относительно неподвижной точки О наз. физ. величина, определяемая векторным произведением: , где – радиус-вектор проведенный из точки 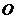в точку .

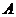Модуль момента импульса: .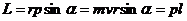

Моментом силыFотносительно неподвижной точки О наз. физ. величина, определяемая векторным произведением радиуса вектора 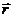, проведенного из точки 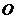в точку 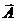приложения силы, на силу : ,

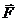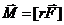Модуль момента силы: 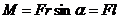, где 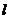– кратчайшее расстояние между линией действия силы и точкой 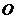– плечо силы.

Момент пары сил: взятое со знаком "плюс" или "минус" произведение модуля сил, образующих пару, на ее плечо. Момент пары сил по­ложителен, если пара стремится вращать тело против часовой стрелки, и отрицателен в противоположном случае.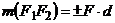

№16

Закон изменения момента импульса.

Рассмотрим произвольную систему тел. Моментом импульса системы назовем величинуL, равную векторной сумме моментов импульсов отдельных ее частей L_i, взятых относительно одной и той же точки выбранной системы отсчета.

L = ΣL_i.

Найдем скорость изменения момента импульса системы. Проведя рассуждения, аналогичные описанию вращательного движения твердого тела, получим, что

скорость изменения момента импульса системы равна векторной сумме моментов внешних сил M, действующих на части этой системы.

dL/dt=M.

Причем вектора L и M задаются относительно одной и той же точки O в выбранной СО.

Закон сохранения импульса.

момент импульса системы тел сохраняется неизменным при любых взаимодействиях внутри системы, если результирующий момент внешних сил, действующих на нее, равен нулю.

№17

Закон всемирного тяготения: между любыми двумя материальными точками действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек (m1 и m2) и обратно пропорциональная квадрату расстояния между ними (r²):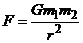

Первой космической(или круговой)
скоростью называют такую минималь-
ную скорость, которую надо сообщить те-
лу, чтобы оно могло двигаться вокруг Зем-
ли по круговой орбите. =>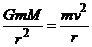

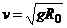
второй космической(или пара-
болической) скоростьюназывают ту
наименьшую скорость, которую надо со-
общить телу, чтобы оно могло преодолеть
притяжение Земли и превратиться в спут-
ник Солнца.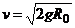

№18

Плоским движением твердого тела называется такое его движение, при котором каждая его точка все время движется в одной и той же плоскости.

Поступательное движение – движение при котором все точки тела движутся одинаково, описывая одинаковые траектории.

№19

Момент инерции - физическая величина, равная сумме произведений масс п материальных точек системы на квадраты их расстояний до рассматриваемой оси.

Уравн. вращательного движения твердого тела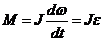

Свободные оси – оси вращения тел, которые не изменяют своей ориентации в пространстве без действия на них внешних сил.

Главные оси – три взаимно перпендикулярные оси, проходящие через центр масс любого тела, которые могут служить свободными осями.

№20.

Расчет момента инерции.

Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом г и внешним - r+dr Момент инерции каждого полого цилиндра dJ=r²dm (так как dr « r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm — масса всего элементарного цилиндра; его объем 2πrhdr. Если ρ — плотность материала, то dm=ρ2πrhdr и dJ=2πρr³hdr. Тогда момент инерции сплошного цилиндра 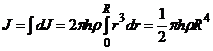, но так как πR²h — объем цилиндра, то его масса m=πR²hρ, а момент инерции J=1/2mR²

Теорема Штейнера. момент инерции тела J относительно любой оси вращения равен моменту его инерции J_C относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями:

№21

Кинетическая энергия вращающегося твердого тела.

№22

Кинетическая энергия твердого тела при плоском движении.

№23

Гироскопы. массивные однородные тела, вращающиеся с большой угловой скоростью около своей оси симметрии, являющейся свободной осью.

Гироскопический эффект.

Применение гироскопа.Гироскопы применяются в различных гироскопических навигационных приборах (гирокомпас, гирогоризонт и т. д.). Другое важное применение гироскопов — поддержание заданного направления движения транспортных средств, например судна (авторулевой) и самолета (автопилот).

№24