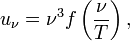Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа.

Абсолютно черное тело. Закон Кирхгофа

Электромагнитное излучение обусловлено, как уже неоднократко отмечалось, колебаниями электрических зарядов, в частности заря­дов, входящих в состав атомов и молекул вещества. Так, например, колебательное и вращательное движения молекул и атомов создают инфракрасное излучение, определенные перемещения электронов в атоме создают видимое и ультрафиолетовое излучение, торможение свободных электронов создает рентгеновское излучение и т. д.

Самым распространенным в природе видом электромагнитного излучения является тепловое излучение, или лучеиспускание; оно со­вершается за счет энергии теплового движения атомов и молекул ве­щества, т. е. за счет внутренней энергии вещества, и потому ведет к охлаждению излучающего тела. Лучеиспускание присуще всем телам при любой температуре, отличной от абсолютного нуля. Теп­ловое излучение имеет сплошной спектр, однако распределение энер­гии в нем существенно зависит от температуры: при низких темпе­ратурах тепловое излучение является преимущественно инфракрас­ным, при высоких температурах — видимым и ультрафиолетовым.

Всякое тело, излучая само, вместе с тем поглощает часть лучис­той энергии, испускаемой другими (окружающими) телами; этот процесс называется лучепоглощением. Он ведет к нагреванию данного тела.

Очевидно, что, теряя энергию путем лучеиспускания и в то же время получая энергию путем лучепоглощения, данное тело должно в конце концов прийти в состояние теплового, или лучистого, равно­весия, при котором потеря энергии за счет лучеиспускания компен­сируется притоком энергии за счет лучепоглощения. Температура, соответствующая этому состоянию, называется температурой лучи­стого равновесия.

Лучистое равновесие является обычным состоянием тел, предо­ставленных самим себе.

Для количественной оценки процессов лучеиспускания и луче­поглощения вводятся следующие характеристики.

Полная лучеиспускательная способность тела Е — величина энер­гии, испускаемой с единицы площади поверхности тела за 1 с; изме­ряется в Дж/(м2-с)*.

Полная лучепоглощательная способность тела А — отношение лу­чистой энергии, поглощаемой телом, ко всей падающей на него лу­чистой энергии; очевидно, что А — безразмерная величина.

Значения Е и А зависят от природы тела и температуры.

* Лучеиспускательную способность иногда называют энергетической све­тимостью.

Опыт показывает, что величина энергии, испускаемой (поглощае­мой) телом, различна для различных длин волн. В связи с этим вво­дится понятие спектральной лучеиспускательной (лучепоглощатель- ной) способности.

Спектральной лучеиспускательной способностью тела Е\ назы­вается лучеиспускательная способность, рассчитанная для узкого интервала длин волн АХ (от X—ДХ/2 до Х+ДХ/2).

Аналогичным образом вводится понятие спектральной лучепоглощательной способности

Лучепоглощательная способность всех реальных тел меньше еди­ницы. Так, например, для видимой части спектра лучепоглощатель­ная способность алюминия равна 0,1, меди—0,5, воды—0,67.

Воображаемое тело, поглощающее при любой температуре всю падающую на него лучистую энергию, называется абсолютно черным телом\ лучепоглощательная способность такого тела для всех длин волн одинакова и равна единице (Лх = А = 1). Для видимой части спектра те­лом, близким по своим свойствам к абсолютно черному, является сажа (А = 0,95).

Практически наиболее совершенным абсолют­но черным телом является малое отверстие в рИс. 352 стенке замкнутой полости, внутренняя поверх­ность которой зачернена (рис. 352). Луч, попав­ший в отверстие, многократно отражается стенками полости и прак­тически не выходит обратно, поскольку при каждом отражении значи­тельная часть его энергии поглощается стенками

Абсолютно черное тело, поглощая падающую на него лучистую энергию, вместе с тем само излучает. Поэтому при низкой температу­ре полости отверстие в ней кажется черным; если же полость на­грета до высокой температуры, то отверстие представляется ярко светящимся. Примерами практически абсолютно черных тел могут служить зрачок глаза и смотровое отверстие мартеновской печи.

Выясним теперь, как связаны между собой лучеиспускательная и лучепоглощательная способности тела. Представим себе изолирован­ную систему из двух тел, имеющих различную температуру и могущих обмениваться энергией только путем лучеиспускания и лучепогло- щения. Через некоторое время в такой системе установится тепловое равновесие. Обозначим лучеиспускательные и лучепоглощательные способности тел при температуре лучистого равновесия соответствен­но через £', Е" и А', А". Предположим, что первое тело испускает с 1 м2 поверхности за 1 с в п раз больше энергии, чем второе, т. е.

£' = пЕ\

Но тогда оно должно и поглощать в п раз больше энергии, чем второе тело, т. е. должно иметь место равенство

А' «= пА"\

в противном случае первое тело начнет нагреваться (или охлаждать­ся) за счет второго тела и его температура будет изменяться, что про­

тиворечит условию теплового равновесий.^Из двух последних равенств следует, что

Е' = Е"

А' ~~ А"

Если изолированная система состоит из многих тел с лучеиспу­скательными способностями £", Е", £"", ... и лучепоглощательными способностями А', А", Л'", ... и одно из них является абсолютно чер­ным, то аналогичные рассуждения приведут к следующему выводу:

где § — лучеиспускательная способность абсолютно черного тела (его лучепоглощательная способность равна единице и потому не на­писана в качестве делителя при 8).

Соотношение (1) представляет собой закон Кирхгофа: для всех тел при данной температуре отношение лучеиспускатель­ной способности к лучепоглощательной способности есть постоянная величина, равная лучеиспускательной способности абсолютно черного тела при той же температуре.

Этот закон остается справедливым и для спектральных лучеиспу­скательной и лучепоглощательной способностей тел:

Из закона Кирхгофа вытекают три важных следствия.

1. Лучеиспускательная способность любого тела при данной тем­пературе равна произведению его лучепоглощательной способности на лучеиспускательную способность абсолютно черного тела при той же температуре:

2. Лучеиспускательная способность любого тела меньше луче­испускательной способности абсолютно черного тела при той же температуре (Е = AS, но Л<1, следовательно, Е<8).

3. Если тело не поглощает каких-либо волн, то оно и не испускает их (Е\ = А\ 8\ у поэтому при = О будет и Е\ = 0).

Соотношения (2) позволяют определять лучеиспускательную спо­собность любого тела, если известна его лучепоглощательная способ­ность А и лучеиспускательная способность абсолютно черного тела 8\ значения А и 8 определяются опытным путем.

Основным источником нагревания почвы является, как известно, солнечное излучение. Изменяя лучепоглощательную способность поверхности почвы пу­тем покрытия этой поверхности различными красителями, можно в довольно значительных пределах регулировать .температуру теплового равновесия верх­него слоя почвы. Этот прием, широко применяемый в агрономической практике, называют мульчированием. В качестве покрытий, носящих общее название

(2)

мульчи, используют молотый мел, торфяной и угольный порошки, битум, ни­грозин и т. п.

Очевидно, что для увеличения лучепоглощательной способности почвы (и, следовательно, для повышения температуры почвы) надо применять темную мульчу, а для уменьшения лучепоглощательной способности почвы (и понижения температуры почвы) — светлую мульчу.

Законы излучения абсолютно черного тела. Гипотеза Планка.

Классический подход

Изначально к решению проблемы были применены чисто классические методы, которые дали ряд важных и верных результатов, однако полностью решить проблему не позволили, приведя в конечном итоге не только к резкому расхождению с экспериментом, но и к внутреннему противоречию — так называемой ультрафиолетовой катастрофе.

Изучение законов излучения абсолютно чёрного тела явилось одной из предпосылок появления квантовой механики.

[править] Первый закон излучения Вина

В 1893 году Вильгельм Вин, воспользовавшись, помимо классической термодинамики, электромагнитной теорией света, вывел следующую формулу:

• 

где u_ν — плотность энергии излучения,

ν — частота излучения,

T — температура излучающего тела,

f — функция, зависящая только от частоты и температуры. Вид этой функции невозможно установить, исходя только из термодинамических соображений.

Первая формула Вина справедлива для всех частот. Любая более конкретная формула (например, закон Планка) должна удовлетворять первой формуле Вина.

Из первой формулы Вина можно вывести закон смещения Вина (закон максимума) и закон Стефана — Больцмана, но нельзя найти значения постоянных, входящих в эти законы.

Исторически именно первый закон Вина назывался законом смещения, но в настоящее время термином «закон смещения Вина» называют закон максимума.

[править] Второй закон излучения Вина

В 1896 году Вин на основе дополнительных предположений вывел второй закон:

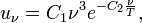
где C₁, C₂ — константы. Опыт показывает, что вторая формула Вина справедлива лишь в пределе высоких частот (малых длин волн). Она является частным конкретным случаем первого закона Вина.

Позже Макс Планк показал, что второй закон Вина следует из закона Планка для больших энергий квантов, а также нашёл постоянные C₁ и C₂. С учётом этого, второй закон Вина можно записать в виде:

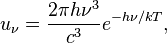
где h — постоянная Планка,

k — постоянная Больцмана,

c — скорость света в вакууме.

[править] Закон Рэлея — Джинса

Основная статья: закон Рэлея — Джинса

Попытка описать излучение абсолютно чёрного тела исходя из классических принципов термодинамики и электродинамики приводит к закону Рэлея — Джинса:

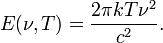
Эта формула предполагает квадратичное возрастание спектральной плотности излучения в зависимости от его частоты. На практике такой закон означал бы невозможность термодинамического равновесия между веществом и излучением, поскольку согласно ему вся тепловая энергия должна была бы перейти в энергию излучения коротковолновой области спектра. Такое гипотетическое явление было названо ультрафиолетовой катастрофой.

Тем не менее закон излучения Рэлея — Джинса справедлив для длинноволновой области спектра и адекватно описывает характер излучения. Объяснить факт такого соответствия можно лишь при использовании квантово-механического подхода, согласно которому излучение происходит дискретно. Исходя из квантовых законов можно получить формулу Планка, которая будет совпадать с формулой Рэлея — Джинса при .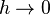

Этот факт является прекрасной иллюстрацией действия принципа соответствия, согласно которому новая физическая теория должна объяснять всё то, что была в состоянии объяснить старая.

[править] Закон Планка

Основная статья: Формула Планка

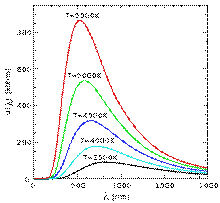
Зависимость мощности излучения чёрного тела от длины волны.

Интенсивность излучения абсолютно чёрного тела в зависимости от температуры и частоты определяется законом Планка:

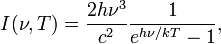
где 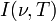— мощность излучения на единицу площади излучающей поверхности в единичном интервале частот в перпендикулярном направлении на единицу телесного угла (размерность в СИ: Дж·с⁻¹·м⁻²·Гц⁻¹·ср⁻¹).

Эквивалентно,

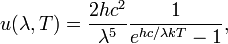
где 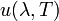— мощность излучения на единицу площади излучающей поверхности в единичном интервале длин волн в перпендикулярном направлении на единицу телесного угла (размерность в СИ: Дж·с⁻¹·м⁻²·м⁻¹·ср⁻¹).

Полная (т.е. испускаемая во всех направлениях) спектральная мощность излучения с единицы поверхности абсолютно чёрного тела описывается этими же формулами с точностью до коэффициента π: ε(ν, T) = πI(ν, T), ε(λ, T) = πu(λ, T)^[1].

[править] Закон Стефана — Больцмана

Основная статья: Закон Стефана — Больцмана

Общая энергия теплового излучения определяется законом Стефана — Больцмана, который гласит:

Мощность излучения абсолютно чёрного тела (интегральная мощность по всему спектру), приходящаяся на единицу площади поверхности, прямо пропорциональна четвёртой степени температуры тела:

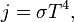
где 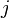— мощность на единицу площади излучающей поверхности, а

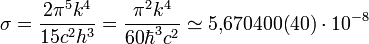Вт/(м²·К⁴) — постоянная Стефана — Больцмана.

Таким образом, абсолютно чёрное тело при 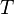= 100 K излучает 5,67 ватт с квадратного метра своей поверхности. При температуре 1000 К мощность излучения увеличивается до 56,7 киловатт с квадратного метра.

Для нечёрных тел можно приближённо записать:

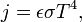
где — степень черноты (для всех веществ 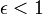, для абсолютно чёрного тела ).

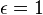Константу Стефана — Больцмана 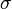можно теоретически вычислить только из квантовых соображений, воспользовавшись формулой Планка. В то же время общий вид формулы может быть получен из классических соображений (что не снимает проблемы ультрафиолетовой катастрофы).

[править] Закон смещения Вина

Длина волны, при которой энергия излучения абсолютно чёрного тела максимальна, определяется законом смещения Вина:

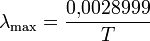
где 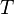— температура в кельвинах, а 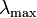— длина волны с максимальной интенсивностью в метрах.

Так, если считать в первом приближении, что кожа человека близка по свойствам к абсолютно чёрному телу, то максимум спектра излучения при температуре 36 °C (309 К) лежит на длине волны 9400 нм (в инфракрасной области спектра).

Видимый цвет абсолютно чёрных тел с разной температурой представлен на диаграмме.

Формула Планка — выражение для спектральной плотности мощности излучения абсолютно чёрного тела, которое было получено Максом Планком. Для плотности энергии излучения :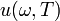

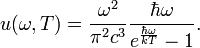
Формула Планка («форма» зависимости 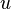от частоты и температуры) первоначально была «выведена» эмпирически. Формула Планка была получена после того, как стало ясно, что формула Рэлея—Джинса, которая следует из классической теории электромагнитного поля, удовлетворительно описывает излучение только в области длинных волн. С убыванием длин волн формула Рэлея—Джинса сильно расходится с эмпирическими данными. Более того, в пределе она даёт расхождение — бесконечную энергию излучения (ультрафиолетовая катастрофа). В связи с этим Планк в 1900 году сделал предположение, противоречащее классической физике, о том, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с частотой излучения выражением:

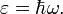
Коэффициент пропорциональности 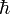впоследствии назвали постоянной Планка, 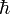= 1.054 · 10⁻²⁷ эрг·с. Это предположение позволило объяснить наблюдаемый спектр излучения теоретически.

Правильность формулы Планка подтверждается не только непосредственной эмпирической проверкой, но и следствиями из данной формулы, в частности из неё следует закон Стефана-Больцмана, также эмпирически подтверждённый. Кроме того, из неё выводятся также и приблизительные формулы, полученные до формулы Планка, — формула Вина и формула Рэлея-Джинса