Мощность, выделяемая в цепи переменного тока. Принцип работы теплового амперметра.
Активной мощностью переменного тока называется средняя за период мощность необратимых преобразований в цепи переменного тока (преобразование энергии электрического тока во внутреннюю энергию): 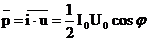 | 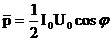 |
или, переходя к действующим значениям, 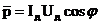 . . | 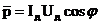 |
Величина 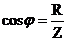 наз. коэффициентом мощности. При малом коэффициенте мощности потребляется лишь малая часть мощности, вырабатываемой генератором. Остальная часть мощности периодически перекачивается от генератора к потребителю и обратно и рассеивается в линиях электропередач. наз. коэффициентом мощности. При малом коэффициенте мощности потребляется лишь малая часть мощности, вырабатываемой генератором. Остальная часть мощности периодически перекачивается от генератора к потребителю и обратно и рассеивается в линиях электропередач. | 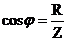 коэффициент мощности коэффициент мощности |
Амперме́тр (см. ампер + …метр от μετρέω — измеряю) — прибор для измерения силы тока в амперах. Шкалу амперметров градуируют в микроамперах, миллиамперах, амперах или килоамперах в соответствии с пределами измерения прибора. В электрическую цепь амперметр включается последовательно с тем участком электрической цепи, силу тока в котором измеряют; для увеличения предела измерений — с шунтом или через трансформатор. (Примером амперметра с трансформатором являются «токовые клещи»)
Принцип действия магнитоэлектрического прибора основан на создании крутящего момента, благодаря взаимодействию между полем постоянного магнита и током, который проходит через обмотку рамки. С рамкой соединена стрелка, которая перемещается по шкале. Угол поворота стрелки пропорционален силе тока.
Электродинамические амперметры состоят из неподвижной и подвижной катушек, соединённых параллельно или последовательно. Взаимодействие между токами, которые проходят через катушки, вызывает отклонения подвижной катушки и соединённой с нею стрелки. В электрическом контуре амперметр соединяется последовательно с нагрузкой, а при высоком напряжении или больших токах — через трансформатор
20. Введение в теорию волновых процессов, основные понятия. Математическое описание синусоидальной волны. Волновое уравнение.
Теория волновых процессов – область науки, исследующая волновые явления различной природы.
С колебаниями и волнами человек встречается постоянно. Существует большое многообразие волновых процессов: волны, порождаемые землетрясениями, звуковые волны, распространяющиеся в воздухе, волны механических колебаний в натянутых струнах музыкальных инструментов или в кристаллах кварца, используемые для стабилизации частоты радиопередатчика, электромагнитные волны, излучаемые антенной, и многие-многие другие. Несмотря на большое разнообразие, в колебательных процессах наблюдаются одни и те же закономерности, которые описываются одинаковыми математическими и физическими моделями и исследуются общими методами.
Синусоидалные волны
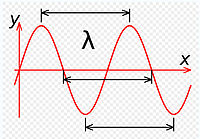

Схема графика синусоидальной волны
Математически, самая основная волна - волна синуса (или гармоническая волна или синусоида), с амплитудой u описанный уравнением:
u(x, t)=Acos(kx−ωt+ϕ) , где:
· A - полуамплитуда волны, половина амплитуды: пика-к-пику, часто называемой просто амплитуда или максимальное расстояние от самого высокого пункта волнения в среде (гребень) к пункту равновесия в течение одного цикла волны. На иллюстрации направо, это - максимальное вертикальное расстояние между основанием и волной;
· x - абсцисса (вектор распространения волны),
· t - координата времени,
· k - пространственная частота,
· ω - временная частота,
· φ - погашение фазы.
Единицы полуамплитуды зависят от типа волны — волн, выраженных через амплитуду как расстояние, например в метрах, от звуковых волн, выраженных через давление и электромагнитных волн, выраженных через амплитуду электрической области (вт/метр).
· λ - длина волны - расстояние между двумя последовательными гребнями (или впалдинами), измеряется в метрах.
· k - пространственная частота волны в радианах аналогиччно при подсчёте из расстояния единицы длины в метрах, может быть связана с длиной волны отношением:
k=2π λ .
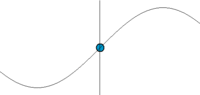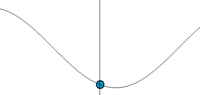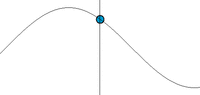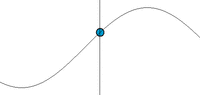

Волны синуса соответствуют простому гармоническому движению.
Период T - время для одного полного цикла колебания волны. Частота f (также часто обозначаемый как ν ) - число периодов в единицу времени (в секунду) и измерена в герц. Они связаны:
f=1 T .
Вообще, частота и период волны - аналоги. Угловая частота ω представляет частоту в радианах в секунду. Это связано с частотой:
ω=2πf=2π T .
Различные местные длины волны на основании гребня-к-гребню в океанской волне, приближающейся к берегу.[4]
Длина волны может быть полезным понятием, даже если волна не является периодической. Например, в океанской волне, приближающейся к берегу, показанному на фигуре, поступающая волна взаимодействует с переменной местной длиной волны, которая зависит частично от глубины морского дна по сравнению с высотой волны. Анализ волны может быть основанным на сравнении местной длины волны с местной водной глубиной.[5]
Хотя произвольные формы волны образуются неизменно без потерь в линейных инвариантных во времени системах, без присутствия дисперсии. Волна синуса - уникальная форма, которая создаётся неизменной, облегчая анализировать фазы и амплитуды.[6],[7]. Функция синуса является периодической, таким образом волна синуса или синусоида имеют длину волны в месте и периоде одновременно.[8],[9] Синусоида и расстояния определяются навсегда, тогда как в физических ситуациях мы обычно имеем дело с волнами, которые существуют для ограниченного диапазона в месте и в промежутке времени
Волновое уравнение в математике — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно линейная: звук в газах, жидкостях и твёрдых телах) и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн. Является одним из основных уравнений математической физики
