Вопрос 17. Частица в одномерной прямоугольной «потенциальной яме» c бесконечно высокими «стенками»

Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)

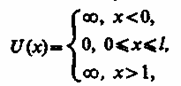
где l - ширина «ямы», а энергия отсчитывается от ее дна (рис. 296).

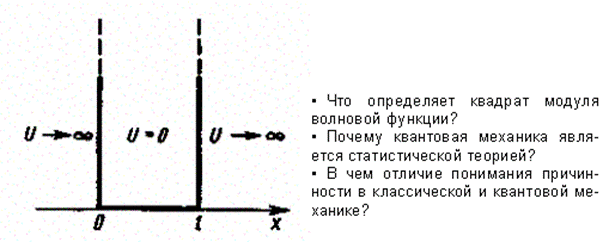
Рис. 296

Уравнение Шредингера (217.5) для стационарных состояний в случае одномерной задачи запишется в виде

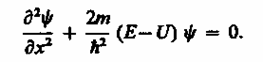
По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х = 0 и х = l)непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид

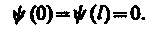(220.2)

В пределах «ямы» (0 £ х £ l) уравнение Шредингера (220.1) сведется к уравнению

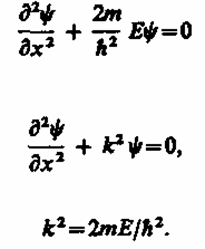
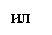
где

Общее решение дифференциального уравнения (220.3):

Y(x) = Asin kx + Bcos kx.

Так как по (220.2) y(x) = 0, то B = 0. Тогда

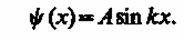(220.5)

Условие (220.2) Y(l) = Asin kl выполняется только при kl = np, где n - целые числа, т. е. необходимо, чтобы

(220.6)

Из выражений (220.4) и (220.6) следует, что

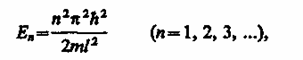(220.7)

т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях , зависящих от целого числа n. Следовательно, энергия E_nчастицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т. е. квантуется. Квантованные значения энергии E_nназываются уровнями энергии, а число л, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне E_n, или, как говорят, частица находится в квантовом состоянии n.

Подставив в (220.5) значение k из (220.6), найдем собственные функции:

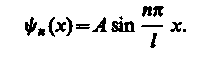
(6)

Эта формула была впервые предложена Максом Планком в 1900г. и называется в его честь. Она полностью соответствует экспериментальным данным для любых длин волн. Легко проверить, что в приближении классической электродинамики Максвелла, т.е. при больших длинах волн, формула Планка переходит в классическую формулу для плотности энергии излучения (2). Более того, сам Планк первоначально фактически угадал формулу (6), анализируя графики экспериментальных кривых . Константа Планка впервые в истории науки появилась именно в этой формуле. Квантовая теория родилась, когда Планк попытался теоретически вывести формулу (6) и обнаружил, что это возможно, только еслипредположить квантование энергии излучения.

Вопрос 18.

Одна из важных задач о движении микрочастиц – это задача о движении гармонического осциллятора - системе, способной совершать гармонические колебания.История квантовой теории реально начинается с Макса Планка, который в 1900 г. получил формулу для правильного описания спектрального распределения теплового излучения. Планк пришел к выводу, что не может обеспечить вывод своей магической формулы для распределения излучения, если только не сделать предположения, которое с философской точки зрения он считал почти неприемлемым. Это предположение заключалось в том, что рассматриваемые им в качестве излучателейгармонические осцилляторы должны обладать энергиями, не распределенными как непрерывные переменные (чего следовало бы ожидать), а принимающими дискретные и регулярным образом расположенные значения. Осцилляторы с частотой υ должны были обладать значениями энергии, которые были бы кратны, т.е. n раз умножены (гдеn = 0,1, 2,3,...) на нечто, названное им квантом энергии hυ.

Рассмотрим одномерный случай. (Трехмерные задачи сложны в математическом отношении, а практически все принципиальные особенности движения микрочастиц можно выявить и на одномерных задачах.) Изменение потенциальной энергии по оси x описывается формулой

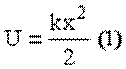
Какие примеры движения окружающего мира хотя бы приближенно описываются такой потенциальной функцией?

· Колебания маятника с малой амплитудой.

· Другой пример – вертикальные колебания грузика, подвешенного на пружине.

В мире микрочастиц примерами могут быть колебания двухатомной молекулы или колебания атомов в кристаллах. Существенным для всех примеров является ограничение движения некоторой областью значений x. Частица не может покинуть параболическую потенциальную яму, края которой уходят на бесконечность.

Из классической механики известно, что проекция движения частицы на ось x представляет собой синусоидальное колебание около положения равновесия x = 0 с частотой:

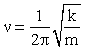
Точки a₀ и -a₀, в которых полная энергия частицы E равна потенциальной энергии, являются для частицы точками поворота. Плотность вероятности обнаружения колеблющейся частицы в различных точках оси x описывается формулой

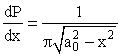
Минимальна вероятность найти частицу около положения равновесия, где она движется с максимальной скоростью. Вблизи точек поворота частица как бы "зависает", и там вероятность обнаружения максимальна.

Какие примеры движения окружающего мира хотя бы приближенно описываются такой потенциальной функцией?

· Колебания маятника с малой амплитудой.

· Другой пример – вертикальные колебания грузика, подвешенного на пружине.

В мире микрочастиц примерами могут быть колебания двухатомной молекулы или колебания атомов в кристаллах. Существенным для всех примеров является ограничение движения некоторой областью значений x. Частица не может покинуть параболическую потенциальную яму, края которой уходят на бесконечность.

Из классической механики известно, что проекция движения частицы на ось x представляет собой синусоидальное колебание около положения равновесия x = 0 с частотой:

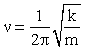
Точки a₀ и -a₀, в которых полная энергия частицы E равна потенциальной энергии, являются для частицы точками поворота. Плотность вероятности обнаружения колеблющейся частицы в различных точках оси x описывается формулой

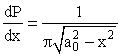
Минимальна вероятность найти частицу около положения равновесия, где она движется с максимальной скоростью. Вблизи точек поворота частица как бы "зависает", и там вероятность обнаружения максимальна.