Вопрос 13. Модель атома водорода по Бору

Закон Планка

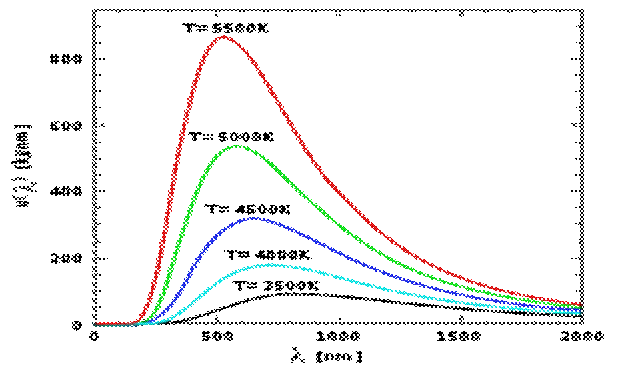
Зависимость мощности излучения чёрного тела от длины волны

Интенсивность излучения абсолютно чёрного тела в зависимости от температуры и частоты определяется законом Планка:

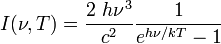
где I(ν,T)dν — мощность излучения на единицу площади излучающей поверхности в диапазоне частот от ν до ν + dν.

Эквивалентно,

,

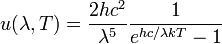где u(λ,T)dλ — мощность излучения на единицу площади излучающей поверхности в диапазоне длин волн от λ до λ + dλ.

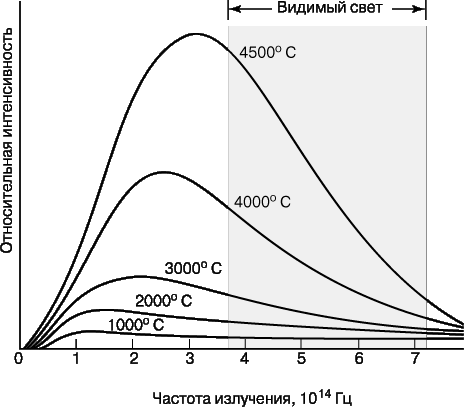
Закон смещения Вина - закон, определяющий положение максимума в распределении энергии в спектре излучения абсолютно черного тела при изменении его температуры.

Закон смещения Вина

Длина волны, при которой энергия излучения абсолютно чёрного тела максимальна, определяется законом смещения Вина:

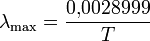
где T — температура в кельвинах, а λ_max — длина волны с максимальной интенсивностью в метрах.

Так, если считать в первом приближении, что кожа человека близка по свойствам к абсолютно чёрному телу, то максимум спектра излучения при температуре 36 °C (309 К) лежит на длине волны 9400 нм (в инфракрасной области спектра).

Видимый цвет абсолютно чёрных тел с разной температурой представлен на диаграмме.

Физический смысл

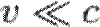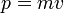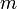Для частиц не очень высокой энергии, движущихся со скоростью (скорости света), импульс равен (где — масса частицы), и 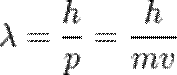. Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость. Например, частице с массой в 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля с 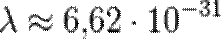м, что лежит за пределами доступной наблюдению области. Поэтому волновые свойства несущественны в механике макроскопических тел. Для электронов же с энергиями от 1 эВ до 10 000 эВ длина волны де Бройля лежит в пределах от ~ 1 нм до 10⁻² нм, то есть в интервале длин волн рентгеновского излучения. Поэтому волновые свойства электронов должны проявляться, например, при их рассеянии на тех же кристаллах, на которых наблюдается дифракция рентгеновских лучей.^[1]

Первое подтверждение гипотезы де Бройля было получено в 1927 году в опытах американских физиков К. Дэвиссона и Л. Джермера. Пучок электронов ускорялся в электрическом поле с разностью потенциалов 100—150 В (энергия таких электронов 100—150 эВ, что соответствует 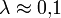нм) и падал на кристалл никеля, играющий роль пространственной дифракционной решётки. Было установлено, что электроны дифрагируют на кристалле, причём именно так, как должно быть для волн, длина которых определяется соотношением де Бройля.^[1]

Подтвержденная на опыте идея де Бройля о двойственной природе микрочастиц — корпускулярно-волновом дуализме — принципиально изменила представления об облике микромира. Поскольку всем микрообъектам (за ними сохраняется термин «частица») присущи и корпускулярные, и волновые свойства, то, очевидно, любую из этих «частиц» нельзя считать ни частицей, ни волной в классическом понимании. Возникла потребность в такой теории, в которой волновые и корпускулярные свойства материи выступали бы не как исключающие, а как взаимно дополняющие друг друга. В основу такой теории — волновой, или квантовой, механики — и легла концепция де Бройля. Это отражается даже в названии «волновая функция» для величины, описывающей в этой теории состояние системы. Квадрат модуля волновой функции определяет вероятность состояния системы, и поэтому о волнах де Бройля часто говорят^[3]как о волнах вероятности (точнее, амплитуд вероятности). Для свободной частицы с точно заданным импульсом p (и энергией 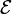), движущейся вдоль оси x, волновая функция имеет вид^[1]:

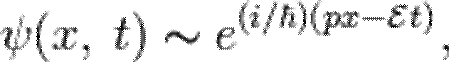
где 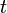— время, .

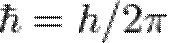В этом случае 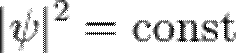, то есть вероятность обнаружить частицу в любой точке одинакова.

Классическая механика основана на законах Ньютона, преобразовании скоростей Галилея и существовании инерциальных систем отсчёт
Границы применимости классической механики

В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.

§ Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий (см.Классическая механика). Адекватным языком для описания свойств атомов и субатомных частиц является квантовая механика. Подчеркнём, что переход от классической к квантовой механике — это не просто замена уравнений движения, а полная перестройка всей совокупности понятий (что такое физическая величина, наблюдаемое, процесс измерения и т. д.)

§ При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности. Опять же, этот переход подразумевает полный пересмотр парадигмы, а не простое видоизменение уравнений движения. Если же, пренебрегая новым взглядом на реальность, попытаться всё же привести уравнение движения к виду F = ma, то придётся вводить тензор масс, компоненты которого растут с ростом скорости. Эта конструкция уже долгое время служит источником многочисленных заблуждений, поэтому пользоваться ей не рекомендуется.

§ Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц (или же большим числом степеней свободы). В этом случае практически целесообразно переходить к статистической физике.

Формулировка Общий случай

В квантовой физике вводится комплекснозначная функция 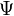, описывающая чистое состояние объекта, которая называется волновой функцией. В наиболее распространенной копенгагенской интерпретации эта функция связана с вероятностью обнаружения объекта в одном из чистых состояний (квадрат модуля волновой функции представляет собой плотность вероятности). Поведение гамильтоновой системы в чистом состоянии полностью описывается с помощью волновой функции.

Отказавшись от описания движения частицы с помощью траекторий, получаемых из законов динамики, и определив вместо этого волновую функцию, необходимо ввести в рассмотрение уравнение, эквивалентное законам Ньютона и дающее рецепт для нахождения 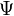в частных физических задачах. Таким уравнением является уравнение Шрёдингера.

Пусть волновая функция задана в N-мерном пространстве, тогда в каждой точке с координатами 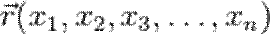, в определенный момент времени t она будет иметь вид 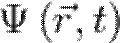. В таком случае уравнение Шрёдингера запишется в виде:

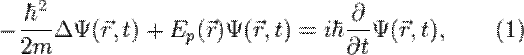
Заряд

Число протонов в ядре 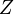определяет непосредственно его электрический заряд, у изотопов одинаковое количество протонов, но разное количество нейтронов. Ядерные свойства изотопов элемента в отличие от химических, могут различаться чрезвычайно резко^[1].

Впервые заряды атомных ядер определил Генри Мозли в 1913 году. Свои экспериментальные наблюдения учёный интерпретировал зависимостью длины волны рентгеновского излучения от некоторой константы 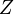, изменяющейся на единицу от элемента к элементу и равной единице для водорода:

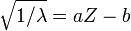, где

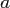и 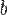— постоянные.

Из чего Мозли сделал вывод, что найденная в его опытах константа атома, определяющая длину волны характеристического рентгеновского излучения и совпадающая с порядковым номером элемента, может быть только зарядом атомного ядра, что стало известно под названием закон Мозли^[2].

Масса

Из-за разницы в числе нейтронов 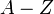изотопы элемента имеют разную массу 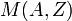, которая является важной характеристикой ядра. В ядерной физике массу ядер принято измерять в атомных единицах массы (а. е. м.), за одну а. е. м. принимают 1/12 часть массы нуклида ¹²C^{[сн 2]}. Следует отметить, что стандартная масса, которая обычно приводится для нуклида — это масса нейтрального атома. Для определения массы ядра нужно из массы атома вычесть сумму масс всех электронов (более точное значение получится, если учесть еще и энергию связи электронов с ядром).

Кроме того, в ядерной физике часто используется энергетический эквивалент массы. Согласно соотношению Эйнштейна, каждому значению массы 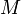соответствует полная энергия:

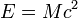, где — скорость света в вакууме.

Соотношение между а. е. м. и её энергетическим эквивалентом в джоулях:

,

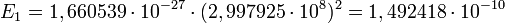а так как 1 электронвольт = 1,602176×10⁻¹⁹ Дж, то энергетический эквивалент а. е. м. в МэВ равен^[1][3]:

.

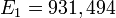[править]Радиус

Анализ распада тяжёлых ядер уточнил оценку Резерфорда^{[сн 3]} и связал радиус ядра с массовым числом простым соотношением:

,

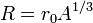где 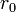— константа.

Так как радиус ядра не является чисто геометрической характеристикой и связан прежде всего с радиусом действия ядерных сил, то значение 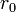зависит от процесса, при анализе которого получено значение 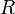, усреднённое значение 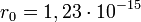м, таким образом радиус ядра в метрах^[1][2]:

.

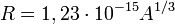Энергия связи

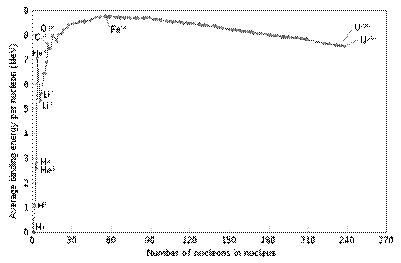
Зависимость средней энергии связи (по оси y) от массового числа (по оси x) ядер.

Большая энергия связи нуклонов, входящих в ядро, говорит о существовании ядерных сил, поскольку известныегравитационные силы слишком малы, чтобы преодолеть взаимное электростатическое отталкивание протонов в ядре. Связь нуклонов осуществляется чрезвычайно короткоживущими силами, которые возникают вследствие непрерывного обмена частицами, называемыми пи-мезонами, между нуклонами в ядре.

Экспериментально было обнаружено, что для всех стабильных ядер масса ядра меньше суммы масс составляющих его нуклонов, взятых по отдельности. Эта разница называется дефектом массы или избытком массы и определяется соотношением:

,

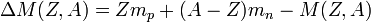где 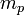и 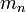— массы свободного протона и нейтрона, 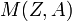— масса ядра.

Согласно принципу эквивалентности массы и энергии дефект массы представляет собой массу, эквивалентную работе, затраченной ядерными силами, чтобы собрать все нуклоны вместе при образовании ядра. Эта величина равна изменению потенциальной энергии нуклонов в результате их объединения в ядро.

Энергия, эквивалентная дефекту массы, называется энергией связи ядра и равна:

,

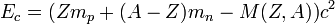где — скорость света в вакууме.

Другим важным параметром ядра является энергия связи, приходящаяся на один нуклон ядра, которую можно вычислить, разделив энергию связи ядра на число содержащихся в нём нуклонов:

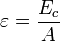
Эта величина представляет собой среднюю энергию, которую нужно затратить, чтобы удалить один нуклон из ядра, или среднее изменение энергии связи ядра, когда свободный протон или нейтрон поглощается в нём.

Как видно из поясняющего рисунка, при малых значениях массовых чисел удельная энергия связи ядер резко возрастает и достигает максимума при 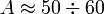(примерно 8,8 Мэв). Нуклиды с такими массовыми числами наиболее устойчивы. С дальнейшим ростом 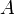средняя энергия связи уменьшается, однако в широком интервале массовых чисел значение энергии почти постоянно ( 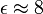МэВ), из чего следует, что можно записать .

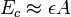Такой характер поведения средней энергии связи указывает на свойство ядерных сил достигать насыщения, то есть на возможность взаимодействия нуклона только с малым числом «партнёров». Если бы ядерные силы не обладали свойством насыщения, то в пределах радиуса действия ядерных сил каждый нуклон взаимодействовал бы с каждым из остальных и энергия взаимодействия была бы пропорциональна 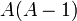, а средняя энергия связи одного нуклона не была бы постоянной у разных ядер, а возрастала бы с ростом .

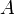Общая закономерность зависимости энергии связи от массового числа описывается формулой Вайцзеккера в рамках теории капельной модели ядра.

Радиоактивность. Лишь небольшая часть нуклидов являются стабильными. В большинстве случаев ядерные силы оказываются неспособны обеспечить их постоянную целостность, и ядра рано или позднораспадаются. Это явление получило название радиоактивности.

Радиоакти́вный распа́д (от лат. radius «луч» и āctīvus «действенный») — спонтанное изменение состава нестабильных атомных ядер (заряда Z,массового числа A) путём испускания элементарных частиц или ядерных фрагментов^[1]. Процесс радиоактивного распада также называютрадиоакти́вностью, а соответствующие элементы радиоактивными. Радиоактивными называют также вещества, содержащие радиоактивные ядра.

Установлено, что радиоактивны все химические элементы с порядковым номером, большим 82 (то есть начиная с висмута), и многие более лёгкие элементы (прометий и технеций не имеют стабильных изотопов, а у некоторых элементов, таких как индий, калий или кальций, часть природных изотопов стабильны, другие же радиоактивны).

Альфа-распад

Основная статья: α-распад

α-распадом называют самопроизвольный распад атомного ядра на дочернее ядро и α-частицу (ядро атома ⁴He).

α-распад, как правило, происходит в тяжёлых ядрах с массовым числом А≥140 (хотя есть несколько исключений). Внутри тяжёлых ядер за счёт свойства насыщения ядерных сил образуются обособленные α-частицы, состоящие из двух протонов и двух нейтронов. Образовавшаяся α-частица подвержена большему действию кулоновских сил отталкивания от протонов ядра, чем отдельные протоны. Одновременно α-частица испытывает меньшее ядерное притяжение к нуклонам ядра, чем остальные нуклоны. Образовавшаяся альфа-частица на границе ядра отражается от потенциального барьера внутрь, однако с некоторой вероятностью она может преодолеть его (см. Туннельный эффект) и вылететь наружу. С уменьшением энергии альфа-частицы проницаемость потенциального барьера экспоненциально уменьшается, поэтому время жизни ядер с меньшей доступной энергией альфа-распада при прочих равных условиях больше.

Правило смещения Содди для α-распада:

.

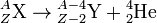Пример:

.

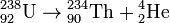В результате α-распада элемент смещается на 2 клетки к началу таблицы Менделеева, массовое число дочернего ядра уменьшается на 4.

]Бета-распад

Основная статья: β-распад

Беккерель доказал, что β-лучи являются потоком электронов. β-распад — это проявление слабого взаимодействия.

β-распад (точнее, бета-минус-распад, β ⁻ -распад) — это радиоактивный распад, сопровождающийся испусканием из ядра электрона и антинейтрино.

β-распад является внутринуклонным процессом. Он происходит вследствие превращения одного из d-кварков в одном из нейтронов ядра в u-кварк; при этом происходит превращение нейтрона в протон с испусканием электрона и антинейтрино:

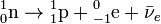
Правило смещения Содди для β ⁻ -распада:

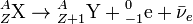
Пример:

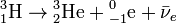
После β ⁻ -распада элемент смещается на 1 клетку к концу таблицы Менделеева (заряд ядра увеличивается на единицу), тогда как массовое число ядра при этом не меняется.

Существуют также другие типы бета-распада. В позитронном распаде (бета-плюс-распаде) ядро испускает позитрон и нейтрино. При этом заряд ядра уменьшается на единицу (ядро смещается на одну клетку к началу таблицы Менделеева). Позитронный распад всегда сопровождается конкурирующим процессом — электронным захватом (когда ядро захватывает электрон из атомной оболочки и испускает нейтрино, при этом заряд ядра также уменьшается на единицу). Однако обратное неверно: многие нуклиды, для которых позитронный распад запрещён, испытывают электронный захват. Наиболее редким из известных типов радиоактивного распада является двойной бета-распад, он обнаружен на сегодня лишь для десяти нуклидов, и периоды полураспадов превышают 10¹⁹ лет. Все типы бета-распада сохраняют массовое число ядра.

[править]Гамма-распад (изомерный переход)

Почти все ядра имеют, кроме основного квантового состояния, дискретный набор возбуждённых состояний с большей энергией (исключением являются ядра ¹H, ²H, ³H и ³He). Возбуждённые состояния могут заселяться при ядерных реакциях либо радиоактивном распаде других ядер. Большинство возбуждённых состояний имеют очень малые времена жизни (менее наносекунды). Однако существуют и достаточно долгоживущие состояния (чьи времена жизни измеряются микросекундами, сутками или годами), которые называются изомерными, хотя граница между ними и короткоживущими состояниями весьма условна. Изомерные состояния ядер, как правило, распадаются в основное состояние (иногда через несколько промежуточных состояний). При этом излучаются один или несколько гамма-квантов; возбуждение ядра может сниматься также посредством вылета конверсионных электронов из атомной оболочки. Изомерные состояния могут распадаться также и посредством обычных бета- и альфа-распадов.

Закон Планка

Зависимость мощности излучения чёрного тела от длины волны

Интенсивность излучения абсолютно чёрного тела в зависимости от температуры и частоты определяется законом Планка:

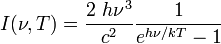
где I(ν,T)dν — мощность излучения на единицу площади излучающей поверхности в диапазоне частот от ν до ν + dν.

Эквивалентно,

,

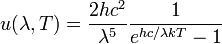где u(λ,T)dλ — мощность излучения на единицу площади излучающей поверхности в диапазоне длин волн от λ до λ + dλ.

Закон смещения Вина - закон, определяющий положение максимума в распределении энергии в спектре излучения абсолютно черного тела при изменении его температуры.

Закон смещения Вина

Длина волны, при которой энергия излучения абсолютно чёрного тела максимальна, определяется законом смещения Вина:

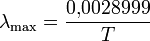
где T — температура в кельвинах, а λ_max — длина волны с максимальной интенсивностью в метрах.

Так, если считать в первом приближении, что кожа человека близка по свойствам к абсолютно чёрному телу, то максимум спектра излучения при температуре 36 °C (309 К) лежит на длине волны 9400 нм (в инфракрасной области спектра).

Видимый цвет абсолютно чёрных тел с разной температурой представлен на диаграмме.

Вопрос 13. Модель атома водорода по Бору

Исходя из этих постулатов и используя планетарную модель строения атома, Н. Бор разработал количественную теорию атома водорода. Он рассчитал радиусы стационарных орбит электрона в атоме водорода и вычислил соответствующие им значения энергии.

Расчет радиусов орбит.' Электрон движется вокруг ядра в атоме водорода по круговой орбите под действием кулоновской силы, которая сообщает

ему центростремительное ускорение. По второму закону Ньютона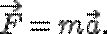

Центростремительное ускорение 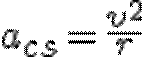электрону сообщает кулоновская сила притяжения со стороны ядра 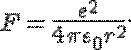Следовательно,

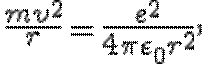откуда 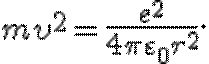(20.1)

Согласно III постулату Бора: 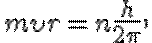отсюда

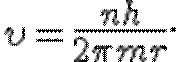(20.2)

Из уравнений (20.1) и (20.2) получим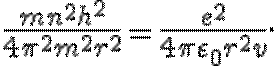

Откуда

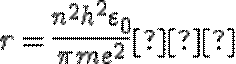(20.3)

выражение для радиусов разрешенных стационарных орбит электрона в атоме водорода. Здесь n — номер орбиты, радиус которой r, 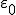— электрическая постоянная, h — постоянная Планка, m — масса электрона, е — заряд электрона.

Мы видим, что радиусы стационарных устойчивых орбит возрастают пропорционально квадратам номеров орбит (рис. 20.3): и т.д. Если электрон в атоме водорода находится на одной из стационарных орбит, то атом обладает определенным значением энергии, определяемой энергией электрона:

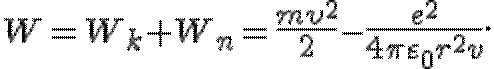
(Знак "-" перед потенциальной энергией означает, что за 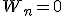принято то значение, которое соответствует 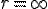). Подставив в эту формулу значения 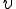и r из формул (20.2) и (20.3), получим:

Таким образом, энергия электрона, находящегося на n-й орбите,

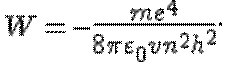(20.4)

Из этой формулы видно, что значения энергии атома водорода квантованы и, чем больше n, тем больше энергия W_n. Для наглядного представления возможных энергетических состояний атомов используются энергетические диаграммы, на которых каждое стационарное состояние атома отмечается горизонтальной линией, называемой энергетическим уровнем (рис. 20.4). Ниже всех на диаграмме располагается энергетический уровень, соответствующий основному состоянию (состояния с минимальной энергией). Энергетические уровни возбужденных состояний располагаются над основным уровнем на расстояниях, пропорциональных разности энергий возбужденного и основного состояний. Переходы атома из одного состояния в другое изображаются вертикальными линиями между соответствующими уровнями на диаграмме. Направление перехода обозначается стрелкой. При переходе электрона с k-й на n-ю орбиту излучается фотон с частотой

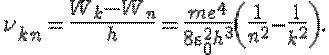
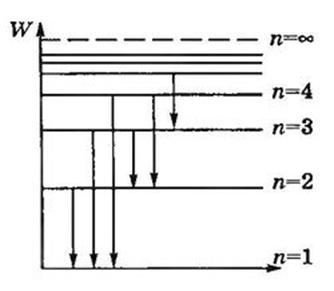
Рис. 20.4

Сравнивая это выражение с эмпирической формулой

(20.5)

видим, что постоянная Ридберга 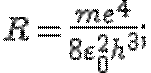следовательно, в формуле (20.5) k — номер орбиты, с которой происходит переход электрона в атоме, n — номер орбиты, на которую переходит электрон.

СПЕКТРАЛЬНЫЕ СЕРИИ

группы спектр. линий в ат. спектрах, частоты к-рых подчиняются определ. закономерностям. В спектрах испускания линии данной С. с. возникают при всех разрешённых излучательных квантовых переходах с разл. начальных возбуждённых уровней энергии на один и тот же конечный уровень и «сходятся» к границе серии, имеющей максимальную для данной серии частоту перехода ((см. АТОМ) рис. 1 в ст. ). Наиболее чётко С. с. выделяются в спектрах водорода и водородоподобных атомов, гелия, щелочных металлов.

Волн. числа линий в С. с. водорода определяются ф-лой:

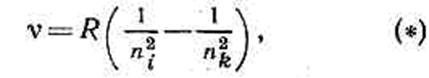
где R — Ридберга постоянная, ni и nk — целые числа, определяющие начальный и конечный уровни энергии. Для каждой С. с. ni постоянно, а числа, определяющие верхние уровни, nk=ni+1, ni+2, . . . Так, для ni=1 и nk=2, 3, ... получается серия Лаймана, частоты линий к-рой лежат в далёкой УФ области; при ni=2, nk=3, 4, . ...— серия Бальмера, её линии лежат в видимой и ближней УФ областях; при ni= 3, nk=4, 5, . . .— серия Пашена, расположенная в ИК области. В далёкой ИК области лежат серии Б рэкета (ni = 4), Пфунда. (ni=5) и Хамфри (ni=6). Ф-ла для С. с. водородоподобных атомов отличается от (*) коэфф. Z2 (Z — ат. номер).

В спектрах щелочных металлов расположение линий описывается более сложными закономерностями. В них выделяются главная, резкая, диффузная и Бергмана серии.

Вопрос 14.Во́лны де Бро́йля — волны, связанные с любыми микрочастицами и отражающие их волновую природу. В 1924 году^[1] французский физик Луи де Бройль высказал гипотезу о том, что установленный ранее^[1] для фотонов корпускулярно-волновой дуализмприсущ всем частицам — электронам, протонам, атомам и так далее, причём количественные соотношения между волновыми и корпускулярными свойствами частиц те же, что и для фотонов. Таким образом, если частица имеет энергию E и импульс, абсолютное значение которого равно p, то с ней связана волна, частота которой ν = E / h и длина волны λ = h / p, где h — постоянная Планка.^[1] Эти волны и получили название волн де Бройля

Физический смысл

Для частиц не очень высокой энергии, движущихся со скоростью 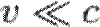(скорости света), импульс равен 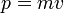(где 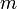— масса частицы), и 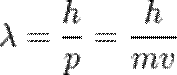. Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость. Например, частице с массой в 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля с 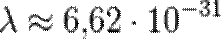м, что лежит за пределами доступной наблюдению области. Поэтому волновые свойства несущественны в механике макроскопических тел. Для электронов же с энергиями от 1 эВ до 10 000 эВ длина волны де Бройля лежит в пределах от ~ 1 нм до 10⁻² нм, то есть в интервале длин волн рентгеновского излучения. Поэтому волновые свойства электронов должны проявляться, например, при их рассеянии на тех же кристаллах, на которых наблюдается дифракция рентгеновских лучей.^[1]

Первое подтверждение гипотезы де Бройля было получено в 1927 году в опытах американских физиков К. Дэвиссона и Л. Джермера. Пучок электронов ускорялся в электрическом поле с разностью потенциалов 100—150 В (энергия таких электронов 100—150 эВ, что соответствует 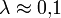нм) и падал на кристалл никеля, играющий роль пространственной дифракционной решётки. Было установлено, что электроны дифрагируют на кристалле, причём именно так, как должно быть для волн, длина которых определяется соотношением де Бройля.^[1]

Подтвержденная на опыте идея де Бройля о двойственной природе микрочастиц — корпускулярно-волновом дуализме — принципиально изменила представления об облике микромира. Поскольку всем микрообъектам (за ними сохраняется термин «частица») присущи и корпускулярные, и волновые свойства, то, очевидно, любую из этих «частиц» нельзя считать ни частицей, ни волной в классическом понимании. Возникла потребность в такой теории, в которой волновые и корпускулярные свойства материи выступали бы не как исключающие, а как взаимно дополняющие друг друга. В основу такой теории — волновой, или квантовой, механики — и легла концепция де Бройля. Это отражается даже в названии «волновая функция» для величины, описывающей в этой теории состояние системы. Квадрат модуля волновой функции определяет вероятность состояния системы, и поэтому о волнах де Бройля часто говорят^[3]как о волнах вероятности (точнее, амплитуд вероятности). Для свободной частицы с точно заданным импульсом p (и энергией 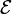), движущейся вдоль оси x, волновая функция имеет вид^[1]:

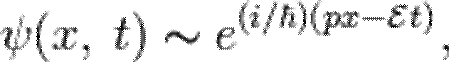
где 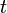— время, .

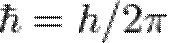В этом случае 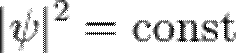, то есть вероятность обнаружить частицу в любой точке одинакова.

Классическая механика основана на законах Ньютона, преобразовании скоростей Галилея и существовании инерциальных систем отсчёт
Границы применимости классической механики

В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.

§ Свойства микромира не могут быть поняты в рамках классической механики. В частности, в сочетании с термодинамикой она порождает ряд противоречий (см.Классическая механика). Адекватным языком для описания свойств атомов и субатомных частиц является квантовая механика. Подчеркнём, что переход от классической к квантовой механике — это не просто замена уравнений движения, а полная перестройка всей совокупности понятий (что такое физическая величина, наблюдаемое, процесс измерения и т. д.)

§ При скоростях, близких к скорости света, классическая механика также перестаёт работать, и необходимо переходить к специальной теории относительности. Опять же, этот переход подразумевает полный пересмотр парадигмы, а не простое видоизменение уравнений движения. Если же, пренебрегая новым взглядом на реальность, попытаться всё же привести уравнение движения к виду F = ma, то придётся вводить тензор масс, компоненты которого растут с ростом скорости. Эта конструкция уже долгое время служит источником многочисленных заблуждений, поэтому пользоваться ей не рекомендуется.

§ Классическая механика становится неэффективной при рассмотрении систем с очень большим числом частиц (или же большим числом степеней свободы). В этом случае практически целесообразно переходить к статистической физике.