Объясните, почему волновая функция должна быть конечной, однозначной и непрерывной.

1)Условие конечности волновой функции. Волновая функция не может принимать бесконечные значения таких, что интеграл расходится; 2)Условие однозначности должна быть однозначной функцией координат и времени, т.к. плотность вероятности обнаружения частиц должна определяться в каждой задаче однозначно; 3)\Условие непрерывности. В любой момент t, волновая функция должна быть непрерывной.

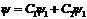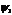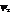33. Запишите принцип суперпозиции для волновых функций. заключается в том, что если система может прибывать в состояниях, описываемых волновой функции и , то она может прибывать в состоянии описываемых волновых функций, где 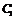и 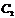- комплексные числа.

2.4. Временное истационарноеуравнения Шредингера

1. Запишите временное уравнение Шредингера.

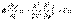
2. Запишите стационарное уравнение Шредингера.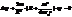

3. Что называют собственным значением энергии? Собственной волновой функцией?

Значения энергии которые имеют место не при любых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи, называется собственным значением энергии.

Собственные значения энергии могут образовывать как непрерывный, так и дискретный ряд.

Решения же, которые соответсвуют собственным значениям энергии, называются собственными функциями.

4. В чем отличие стационарного и временного уравнений Шредингера?

В стационарном уравнении Шредингера исключается зависимость Ψ от времени, и называется стационарным состоянием-состояние с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частица движется стационарно, т.е. функция U=U(x,y,z) не зависит явно от времени и имеет смысл потенциальной энергии.

5. Граничные условия для частицы в потенциальной яме с бесконечно высокими стенками.

На границах «ямы» (при х=0 и х=0) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид: Ψ(0)=Ψ(l)=0

6. Собственная волновая функция частицы в одномерном потенциальном ящике имеет вид 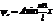. Как можно определить коэффициент пропорциональности А в этом выражении?

Постоянную интегрирования А найдем из условия нормировки, которое для данного случая запишется в виде:

А²∫sin²(nπ/l)xdx=1

В результате интегрирования получим А=√2/l

7. Собственные значения энергии частицы в одномерном потенциальном ящике имеют вид 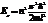. Каково расстояние между 3-м и 4-м энергетическими уровнями?

∆Е=E4-E3=(π²h²/2ml²)(2*4-1)=49π²h²/ml²

8. Собственные значения энергии частицы в одномерном потенциальном ящике имеют вид 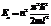. Каково расстояние между 1-м и 2-м энергетическими уровнями?

∆Е=E2-E1=(π²h²/2ml²)(2*2-1)=9π²h²/ml²

9. Собственные значения энергии частицы в одномерном потенциальном ящике имеют вид 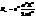. Во сколько раз отличаются значения энергии электрона и протона, находящихся в одинаковых ящиках?

m(электр)=9,1095*10(-31)кг

m(протон)=1,673*10(-27)кг

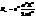
π²h²=10,976*10(-68)

h/2π=1,0545*10(-34)

Е(электр)=0,602*10(-35)пДж

Е(протон)=3,28*10(-39)пДж

Е(электр)/ Е(протон)=1,8*10(3)пДж

10. Собственные значения энергии частицы в одномерном потенциальном ящике имеют вид 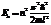. Как изменится энергия электрона в основном состоянии, если ширину ящика уменьшить в 2 раза.

Следуя формуле можно определить, как изменится энергия, в данном случае энергия должна увеличиться в 4 раза

11. Квантовая частица в бесконечно глубокой прямоугольной одномерной потенциальной яме имеет дискретный энергетический спектр (энергия частицы квантована). Как зависит эта энергия от значения квантового числа n?

Движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Е зависящих от целого числа n. Следовательно, энергия Е частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т.е.квантуется. Квантованные значения энергии Е называются уровнями энергии, а число n, определяющие энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне Е или, как говорят, частица находится в квантовом состоянии n.

12. Чему равна величина Dy в уравнении Шредингера ?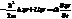

Dy- оператор Лапласа (d²Ψ∕dх²_+ d²Ψ∕dу²+ d²Ψ∕dz²)

13. Что называют туннельным эффектом?

Туннельный эффект -квантовое явлений, в результате которого микрообъект может «пройти» сквозь потенциальный барьер.

Суть туннельного эффекта заключается в прохождении частицы сквозь потенциальный барьер и возможности её обнаружения в области запрещенной с точки зрения классической механики.

14. На рисунке показана зависимость квадрата модуля волновой функции, 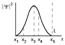определяющей состояние электрона в одномерной «потенциальной яме» шириной L в квантовом состоянии при n = 1. Какая из указанных координат соответствует состоянию, в котором вероятность обнаружить электрон наибольшая?

С увеличением квадрата модуля функции, т.е. с увеличением модуля амплитуды волн де Бройля увеличивается вероятность обнаружить электрон наибольшая. Следовательно в х3 вероятность больше.

15. Энергия электрона в одномерной «потенциальной яме» шириной l определяется формулой 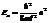. Как изменяется относительный энергетический интервал между уровнями 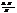при возрастании квантового числа n?

∆Е/Е-?

∆Е=(π²h²/8ml²)(2n+1)

Е=(π²h²n²/8ml²)можно заменить коэффициентом k.

∆Е/Е=k(n+1)²-kn²/kn²=2n+1/n²

подставляя значение в n, можно узнать как изменяется энергия с возрастанием n

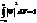-условие нормировки