Оптика. 1.1. Свет как электромагнитные волны. Геометрическая оптика

Интерференция света

Что собой представляет волновой пакет?

Суперпозиция волн, малоотличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства.

Что называют групповой скоростью?

Скорость перемещения интерференционной картины, образованной группой волн различных частот, распространяющихся в одном направлении. Она не имеет отношение к переносу энергии этими волнами.

Какой свет называется монохроматическим?

Монохроматические волны – строго синусоидальная волна с постоянным во времени циклической частотой (ω) и амплитудой (а) и начальной фазой (ф). Амплитуда и фаза могут меняться от одной точки пространства к другой, частота одна и та же для колебательного процесса во всем пространстве. Монохроматическое колебание в каждой точке пространства длится бесконечно во времени. Поэтому строго монохроматические волны не могут быть точно реализованы на практике.

Что называется интерференцией?

Интерференция –явление наложения когерентных волн, при котором, в зависимости от соотношения фаз складываемых волн происходит их усиление или ослабление, т.е. происходит перераспределение интенсивностей налагаемых волн.

Как выглядит интерференционная картина от красного источника?

Т.к. красный свет является монохроматическим, то интерференционная картина будет представлять собой чередование светлых и темных полос.

Условие максимума.

Если на оптической разности хода двух интерферирующих волн наблюдается четное число полуволн, то тогда наблюдается максимум интерференционной картины.

Условие максимума: cos (∆φ)= +1 при ∆φ=2mπ

∆s = (ln-l₁n) = ∆ln=(λ/2π) * ∆φ= (λ/2π)*2πm= 2m* λ/2

Условие минимума.

Если на оптической разности хода двух интерферирующих волн наблюдается нечетное число полуволн, то тогда наблюдается минимум интерференционной картины.

Условие минимума: cos (∆φ)= -1 при ∆φ=(2m+1)π

∆s = (l₂n-l₁n) = ∆ln=(λ/2π) * ∆φ= (λ/2π)*(2m+1)π= (2m+1)* λ/2

Докажите, что при интерференции двух одинаковых по интенсивности волн в максимуме наблюдается учетверение интенсивности.

φ₂ – φ₁=0 cos0=1 I=I₂+I₁

(√ I₂I₁) cos (φ₂ – φ₁)= I₁ + I₁ + 2I₂ = 4I

9.Какие волны называются когерентными?

Волны, у которых разность фаз возбуждаемые колебаниями, остается постоянной во времени, называются когерентными.

Что такое длина когерентности?

Расстояние, которое волна пройдет до тех пор, пока ее фаза не изменится на π. l_к = v t_к /n

Что называется временем когерентности?

Среднее время (t_к), в течение которого амплитуда, начальная фаза колебаний и частота остаются неизменными.

Почему при наложении двух пучков естественного света не наблюдается интерференционной картины?

Пучки должны быть когерентными.

Что называют оптическим путем луча?

Оптическим путем луча называется произведение геометрической длины пути (l) световой волны в среде на абсолютный показатель преломления света (n): S=nl

14. При какой разности фаз складываемых колебаний наблюдается интерференционный максимум?∆φ=2mπ

При какой разности фаз складываемых колебаний наблюдается интерференционный минимум?∆φ=(2m+1)π

Объясните, почему при наблюдении интерференции в тонких плёнках на просвет и на отражение максимумы и минимумы меняются местами.

Разность хода между лучами определяется удвоенной длиной AD и участком ВС. Однако следует иметь в виду, что пленка является более плотной оптической средой, и скорость света в ней меньше. Вследствие этого время, затрачиваемое светом на прохождение пути AD, будет больше в n раз, где n – показатель преломления пленки. Поэтому принято говорить об оптической длине пути света, которая равна ADn. Теперь разность оптических путей лучей 1 и 2 D = 2n(AD) – BC +l/2.Величина l/2 добавляется потому, что происходит изменение фазы волны на 180 ⁰, что эквивалентно увеличению пути на l/2. Если D= (2n-1)l/2, то 2DFncosb =nl cсоответствует условию минимума освещенности, а D= =nl= 2DFncosb +l/2 – условию максимума. Рисунок

Чем объясняется разнообразие окраски крыльев бабочек, хотя красящий пигмент в них отсутствует?

Исходя из условия максимума: 2d(√n² - sin²α) + λ/2 = λ/2π * 2mπ или

2d(√n² - sin²α) = (2m-1) λ/2

Исходя из условий минимума: 2d(√n² - sin²α) + λ/2 = λ/2π * (2m+1) или

2d(√n² - sin²α) = mλ

Условия интерференционных максимумов и минимумов для разных длин волн в отраженном свете будет выполняться на участках пленки с различной толщиной. Именно этим, а вовсе не наличием красящего пигмента, и объясняется радужная окраска крыльев бабочек.

В опыте Юнга на пути одного из интерферирующих лучей помещалась тонкая стеклянная пластинка. Вследствие чего центральная светлая полоса смещалась в положение, первоначально занятое пятой светлой полосой (не считая центральной). Луч падает перпендикулярно к поверхности пластинки. Показатель преломления пластинки 1,5, длина волны 600 Нм. Какова толщина пластинки.

∆S=2d (n-1)= mλ. При m=5.ответ: 1200*10^{-9 м. или 1,2 мкм}

Дифракция волн

Сформулируйте принцип Гюйгенса-Френеля. Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн или

(световая волна, возбужденная каким-либо источником может быть представлена как результат суперпозиции когерентных вторичных волн, излучаемых вторичными источниками- бесконечно малыми элементами любой волновой поверхности, охват этот источник )

3. Объясните попадание света в область геометрической тени с помощью принципа Гюйгенса. Каждая точка, выделяемого отверстием участка волнового фронта, служит источником вторичных волн, кот огибает края отверстия. (все точки этого волнового фронта будут являться когерентными источниками сферических вторичных волн, распространяющихся в сторону движения волнового фронта)

Что такое дифракция?

Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды.(случай дифракции, если волновые фронты плоские , лучи параллельные, и дифр картина наблюдается на бескон большом расстоянии – для этого необходимы линзы)

6. В чем заключается метод зон Френеля?Разбиение волновой поверхности S на зоны, границы первой (центр) зоны служат точки поверхности S наход на расстоянии l+λ\2 от точки M. Точки сферы наход на расстоянии l+2λ\2, l+3λ\2 от точки M, образ зоны Френеля. При наложении этих колебаний они взаимно ослаб друг друга A=A₁-A₂+A₃-A₄…+A_i С увелич номера зоны,уменьш интенсивность излучения зоны в насправлении т.M, т.е уменьш A_i A₁>A_i>A₃…>A_i

7. Почему в методе зон Френеля они выбираются таким образом, чтобы расстояния от соседних зон различались на l/2?

Векторы напряженности электрического (Е) и магнитного (Н) поля в электромагнитной (световой) волне взаимноперпендикулярны, а нормаль к проходящей через них плоскости совпадает с направлением распространения волны. Поскольку колебания векторов Е и Н осуществляются перпендикулярно направлению распространения волны, световая волна является поперечной. Плоскость, в которой колеблется вектор Н называется плоскостью колебания волны, а плоскость Е – плоскостью поляризации. В поляризованном световой волне колебания проходят строго в одном направлении. Рисунок с методички

Закон Малюса.

I = I₀cos²φ

Интенсивность света, прошедшего через поляризатор, равна произведению, падающего на поляризатор световой волны и квадрата косинуса угла между плоскостью поляризации световой волны, падающий на поляризатор и плоскостью пропускания поляризатора.

Изобразите на графике зависимости интенсивности прошедшего через поляризатор света от квадрата косинуса угла между плоскостью поляризации падающего света и плоскостью пропускания поляризатора. прямая зависимость

Интенсивность света, прошедшего через поляризатор, равна произведению, падающего на поляризатор световой волны и квадрата косинуса угла между плоскостью поляризации световой волны, падающий на поляризатор и плоскостью пропускания поляризатора.

Полное преломление – это эффект, проявляющийся при падении продольных плоскополяризованных волн на границе раздела разнородных сред, и заключающийся в отсутствии отраженной волны. Эффект возможно наблюдать только в случае падения потока вертикально-поляризованной волны (направление вектора напряженности электромагнитного поля – в плоскости падения) на границу раздела сред под углом Брюстера. При этом, согласно, закону преломления, в отраженном потоке будет содержаться только горизонтальной поляризованной составляющей, а т.к. падающий поток не содержал горизонтально поляризованных волн, то энергия отраженного потока будет равна нулю.Таким образом, вся энергия падающего потока будет в преломленных волнах.

9. Угол Брюстера при падении света из воздуха на кристалл каменной соли равен 60°. Найти скорость света в этом кристалле (с — скорость света в вакууме).

Tg θ_Б = n₂/n₁, n₁=c/v₁, n₂=c/v₂, Tg θ_Б = v₁/v₂, т.к. первая среда воздух, то v₁=с=3*10⁸ м/с, tg θ_Б=c/v₂, v₂=c/ tg θ_Б = 3*10⁸/√3 = 1,8 * 10⁸ м/с

Двойным лучепреломлением обладают все прозрачные кристаллы, т.е. раздваивание каждого падающего на них светового пучка. Способность веществ расщеплять падающих световой луч на 2 луча – обыкновенный и необыкновенный, которые распространяются в различных направлениях с различной фазовой скоростью и

Исландского шпата направить узкий пучок света, то из кристалла выйдут два пространственно разделенных луча, параллельных друг другу и падающему лучу. Когда первичный пучок падает на кристалл нормально, преломленный пучок разделяется на два, причем один из них является продолжением первичного, а второй отклоняется. Второй из них получил название необыкновенного, а первый-обыкновенный.

Происходящее вследствие зависимости показателя преломления среды от направления напряженности электрического поля световой волны. Световая волна в анизотропных веществах распадается на 2 волны – обыкновенную и необыкновенную с взаимно перпендикулярными плоскостями поляризации света.

Направление в анизотропном кристалле, по которому луч света распространяется, не испытывая двойного лучепреломления. Любая прямая, проходящая параллельно данному направлению является оптической осью. В зависимости от типа, кристаллы бывают двуосные и одноосные, т.е. иметь 2 или одну оптическую ось.

При прохождении через оптическую ось кристалла. Свет падает нормально на плоскую поверхность оптически отрицательного одноосного кристалла, оптическая ось которого параллельна ей. Оптическая ось лежит в ней. В этом случае необыкновенный луч не преломляется, а совпадает по направлению с падающим и обыкновенным.

Параллельный пучок света переходит из глицерина в стекло так, что пучок, отражённый от границы раздела этих сред, оказывается максимально поляризованным. Определить угол между падающим и преломлённым пучками. Абсолютные показатели преломления глицерина и стекла 1,45 и 1,5 соответственно.

1.5/1.45=1.07=tgα(следует)α=arctg1.07= 47⁰ –падающий луч

sin47/1.07=0.68 arcsin0.68=43⁰ – преломленный луч

27.Пластинку кварца толщиной d = 2 мм поместили между параллельными николями, в результате чего плоскость поляризации монохроматического света повернулась на угол a = 45^o. Какой наименьшей толщины d_min следует взять пластинку, чтобы поле зрения поляриметра стало совершенно тёмным?

Угол поворота равен: φ= αd.(для кристаллов и прозрачных веществ). Поле будет темным при φ= 90⁰ Значит, нам необходимо повернуть пластинку еще на 45⁰ , для того, чтобы они были взаимно перпендикулярны. Тогда d_min=d+d. Ответ: 4 мм.

28. Кварцевую пластинку поместили между скрещенными николями. При какой наименьшей толщине d_min кварцевой пластины поле зрения между николями будет максимально просветлено? Постоянная вращения [a] для кварца равна 27 град/мм.

Угол поворота равен: φ= [α]d(для кристаллов и прозрачных веществ). φ= 90⁰ . Тогда d_min = φ/[α]

29. Угол между плоскостями поляризации поляризатора и анализатора составляет 45^о. Во сколько раз ослабляется естественный свет, проходя через такую систему?

α =45^о. I = I₀cos²α, cos²α= I/ I₀ I/I₀ = ½ k= I₀/I = 2. В 2 раза

Тепловое излучение

1. Что называют энергетической светимостью?

Энергетическая светимость – величина, численно равная энергии, излучаемой единицей поверхности тела в единицу времени во всем диапазоне длин волн.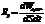

2. Что называют спектральной плотностью энергетической светимости?

Излучательная способность (спектральная плотность энергетической светимости) – величина, численно равная энергии, излученной единицей поверхности вещества в единицу времени в единичном диапозоне длин волн.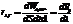

3. Что такое коэффициент поглощения?

Коэффициент поглощения (поглощающая способность тела)– величина, равная отношению энергии поглощенного света, к энергии падающего.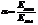

4. Что такое коэффициент отражения?

Коэффициент отражения (отражательная способность тела) — величина, равная отношению энергии отраженного света, к энергии падающего.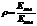

5. Закон Кирхгофа для теплового излучения.

Для всех тел, независимо от их природы, отношение излучательной способности к спектральному коэффициенту поглощения, при той же температуре и для тех же длин волн, есть универсальная функция от длины волны и температуры ,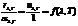

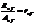
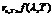- универсальная функция Кирхгофа

Универсальная функция Кирхгофа есть излучательная способность абсолютно черного тела, т.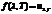е. , где 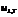- излучательная способность АЧТ.

Поэтому отношение излучательной способности любого тела к его спектральному коэффициенту поглощения равно излучательной способности АЧТ для той же длины волны и при той же температуре

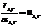(дифференциальная форма закона Кирхгофа)

Отношение светимости серых тел к их коэффициенту поглощения есть универсальная (общая для всех серых тел) функция температуры:

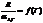(интегральная форма закона Кирхгофа)

где R относится ко всему спектру излучения при данной температуре

6. Каков физический смысл универсальной функции Кирхгофа?Универсальная функция Кирхгофа есть излучательная способность абсолютно черного тела, т.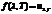е. , где 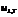- излучательная способность АЧТ.

Поэтому отношение излучательной способности любого тела к его спектральному коэффициенту поглощения равно излучательной способности АЧТ для той же длины волны и при той же температуре

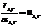(дифференциальная форма закона Кирхгофа)

Отношение светимости серых тел к их коэффициенту поглощения есть универсальная (общая для всех серых тел) функция температуры:

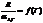(интегральная форма закона Кирхгофа)

где R относится ко всему спектру излучения при данной температуре

7. Что называют абсолютно черным телом?

АЧТ – тело, способное поглощать полностью при любой температуре все падающее на него излучение любой частоты. Спектральная поглощающая способность: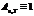

8. Какое тело называют серым?

Серое тело - тело, поглощательная способность которого меньше единицы, но одинакова для всех частот и зависит только от температуры. Спектральная поглощающая способность: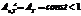

9. Закон Стефана-Больцмана.

Энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры

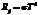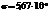
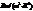, (постоянная Стефана-Больцмана)

10. Закон смещения Вина.

Длина волны 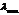, соответствующая максимуму спектральной плотности энергетической светимости черного тела, обратно пропорциональна его термодинамической температуре

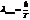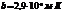, (постоянная Вина)

11. Нарисуйте графики зависимости спектральной плотности энергетической светимости абсолютно черного тела u(l,T) от длины волны для двух разных значений температуры и укажите, какой из них соответствует большей температуре.

С ростом температуры максимум интенсивности излучения смещается в сторону более коротких длин волн(влево). При увеличении температуры растет и амплитуда интенсивности излучения.

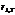
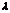
12. Закон Релея-Джинса.

Релй и Джинс применили законы классической физики к тепловому излучению и получили аналитическое выражение для функции Кирхгофа:

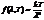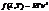, . В области больших длин волн приводят к абсурдному результату. В области коротких волн излучательная способность АЧТ по теоретическим расчетам увеличивается и энергетическая светимость АЧТ при любой температуре стремится к бесконечности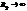

13. Какая энергия излучается за 1 мин с 16 см² абсолютно чёрного тела, если максимум спектральной плотности энергетической светимости приходится на длину волны 0,58 мкм?

λ_max=b/T - по первому закону Вина Где b - первая постоянная Вина Из первого закона Вина:T=λ_max/ b, где λ_max - длина волны, на которую приходится максимум спектральной плотности. T=0.58*10^-6/2.898^-3=0.2*10^-3 K. Энергетическая светимость тела:Re=Фe/S , где Фе – поток излучения Учтя, что Фе=W/t, получим Re=W/(St), Re можно также выразить из закона Стефана- Больцмана. Re=σT⁴ где σ – постоянная Стефана Больцмана Приравняем: σT⁴=W/(St) откуда W=σT⁴*St=5.67*10⁸*0.2⁴*10^-12*16*10⁴*60=8.64*10^-24 Дж

14. При какой температуре максимум спектральной плотности энергетической светимости абсолютно чёрного тела приходится на длину волны 0,642 мкм?

λ_max=C^’/T-по первому закону Вина. Где C^’-первая постоянная Вина. T=λ_max/C^’=0,642*10^-6/2,898*10^-3=0,22*10^-3 K

15. Определите, как и во сколько раз изменится мощность излучения черного тела, если длина волны, соответствующая максимуму его спектральной плотности энергетической светимости, сместилась с l₁=720 нм до l₂=400 нм.

λ_max=C^’/T-по первому закону Вина T=λ_max/C^’

Мощность излучения черного тела: P=Re*S=σT⁴*S

Где σ- постоянная Стефана – Больцмана.

P₂/P₁=(σT₂⁴S)/(σT₁⁴S)= T₂⁴/ T₁⁴=λ₁⁴/λ₂⁴=269/25.6=10.5

16. Черное тело нагрели от температуры Т₁=600 К до Т₂=2400 К. Определите, на сколько изменилась длина волны, соответствующая максимуму спектральной плотности энергетической светимости.

λ_max=C^’/T-по первому закону Вина. Где C^’-первая постоянная Вина.

λ_1max=2.898*10^-3/600=0.483*10^{-5 м}

λ_2max=2.898*10^-3/2400=0.12*10^{-5 м}

λ_1max/ λ_2max=0.483*10^-5 /0.12*10^-5=4.025

λ_1max(больше)λ_2max в 4,025 раза, т.е с нагреванием длина волны уменьшилась в 4,025 раза.

17. Имеется два абсолютно черных источника теплового излучения. Температура одного из них 2500 К. Найти температуру другого источника, если длина волны, отвечающая максимуму его испускательной (излучательной) способности, на 0,5 мкм больше длины волны, соответствующей максимуму испускательной способности первого источника.

λ_1max=C^’/T₁=2,898*10^-3/2500=1,2*10^{-6 м}

λ_2max= λ_1max+0,5*10^-6

λ_2max=C^’/T₂ откуда T₂= C^’/( λ_1max+0,5*10^-6)=2.898*10^-3/1.7*10^-6=1.7*10³ K

18. Чему равна длина волны, на которую приходится максимум излучения абсолютно черного тела с температурой Т = 1000 К?

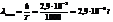
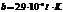
19. Длина волны, на которую приходится максимум излучения абсолютно черного тела, равна 1 мкм. Определить температуру тела.

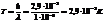
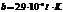
20. Черное тело находится при температуре Т₁ = 10⁴К. При остывании тела длина волны, соответствующая максимуму спектральной плотности энергетической светимости, изменилась на Dl=1 мкм. Определить температуру Т₂, до которой тело охладилось.

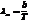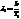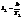Из 1-го закона Вина, . (1) и (2).

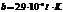
Изменение длины волны, на который приходится максимум спектральной плоскости энергетической светимости, 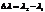(3). Подставляя (1) и (2) в (3), получаем 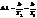откуда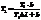

21. При какой температуре энергетическая светимость абсолютно черного тела равна 1 Вт/м²?

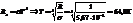
22. Во сколько раз надо увеличить абсолютную температуру АЧТ, чтобы его энергетическая светимость возросла в 9 раз?

, ,

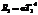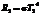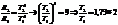
23. Определить диаметр нити накала электрической лампы, если мощность электрического тока, питающего лампу, равна 1000 Вт, длина нити 10 см, температура 3000 К. Считать, что излучение нити соответствует излучению АЧТ.

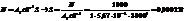
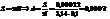
24. Какой поток энергии получает комната через открытую дверцу печи, в которой поддерживается температура 1000 К? Размер дверцы 10´15 см. Считать, что отверстие печи излучает как черное тело.

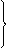
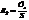
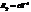
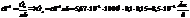
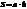
25. С поверхности сажи площадью 1 см² при температуре 400⁰С за 1 мин излучается энергия 1000 Дж. Определить коэффициент черноты сажи.

.

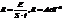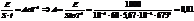
26. Мощность излучения шара радиусом 10 см при некоторой постоянной температуре равна 1 кВт. Найти эту температуру Т, считая шар серым телом с коэффициентом черноты 0,1.

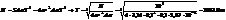
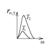
27. Площадь, ограниченная графиком спектральной плотности энергет. светимости черн. тела, при переходе от темп-ры Т₁ к темп-ре Т₂ увеличилась в 16 раз. Во сколько раз возросла темп-ра?

,

, , ,

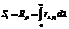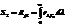
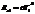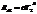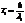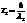
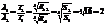
28. Поток энергии, излучаемой из смотрового окошка плавильной печи, равен 34,6 Вт. Опр-ть температуру печи, если площадь отверстия 6,1 см².

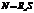(1). По закону Стефана-Больцмана 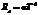(2). Подставляя (2) в (1), получим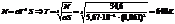

29. Мощность излучения абсолютно черного тела 10 кВт. Найти площадь излучающей поверхности тела, если максимум спектральной плотности его энергетической светимости приходится на длину волны 700 нм.

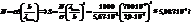
30. Вследствие изменения температуры абсолютно черного тела максимум спектральной плотности энергетической светимости сместился с 2,4 мкм на 0,8 мкм. Как и во сколько раз измен-сь энергетич. светимость тела?

, ,

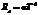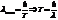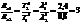
31. Опр-ть температуру и энергетич. светимость абсолютно черного тела, если максимум энергии излучения приходится на длину волны 600 нм.

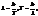
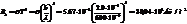
32. Из смотрового окошечка печи излучается поток 4 кДж/мин. Определить температуру печи, если площадь окошечка 8 см².

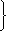
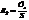
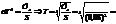
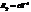
33. Вычислить истинную температуру вольфрамовой раскаленной нити, если радиационный пирометр показывает температуру 2,5 кК. Принять, что поглощательная способность для вольфрама 0,35.

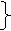
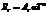
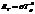
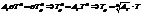
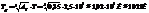
34. Поток излучения абсолютно черного тела 10 кВт. Максимум энергии излучения приходится на длину 0,8 мкм. Определить площадь излучающей поверхности.

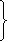
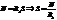
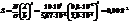
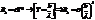
35. Запишите выражение для массы фотона. m=hν/c²

36. Запишите выражение для энергии фотона. W=hν

37. Запишите выражение для импульса фотона. p=ε₀/c=hν/c

38. Чему равна длина волны излучения, соответствующая фотонам с энергией 3эВ?

Энергия фотона: ε=hν откуда ν=ε/h

Длина волны: λ=C/ν=(Ch)/ε где ε - энергия фотона

λ=(3*10⁸*6.62*10^-34)/(3*1.6*10^-19)=4.14*10^{-7 м}

39. Определить импульс фотона красного излучения, длина волны которого 720 нм.

импульс фотона: p=h/λ=6.62*10^-34/720*10^-9=0.0092*10^-25 (Дж*с)/м

40. Чему равна частота света, соответствующая фотонам с энергией
50·10^–19Дж?

Энергия фотона: ε=hν откуда ν=ε/h=50*10^-19/6,62*10^-34=7,55*10¹⁵ Гц

41. Как изменится импульс фотона с увеличением частоты световой волны в 2 раза?

Импульс фотона уменьшится в два раза:p₁=h/λ;p₂=h/2λ; p₁/p₂=(h/λ)(2λ/h)=2

42. Чему равна масса фотона видимого света, длина волны кот-го 500 нм?

Масса фотона: m=(hν)/c², учтя, что с=λν, получим m=h/(cλ)

m=6.62*10^-34/3*10⁸*500*10^-9=0.0044*10^{-33 кг}

43. Найдите массу фотона красного света с длиной волны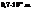

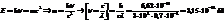
44. Определите длину волны фотона, энергия которого равна кинетической энергии электрона, прошедшего из состояния покоя ускоряющую разность потенциалов 3,3 В.

eU=(m_eυ²)/2 откуда υ=корню из ((2eU)/m_e). Энергия электрона: ε_e=m_ec². ε=ε_e Энергия фотона:ε=hν=(hυ)/λ , откуда λ=(hυ)/ε=((корень из((2eU)/m_e))/ m_ec²)*h =0,087*10^{-13 м.}

45. Опр. частоту кол-й свет.волны, масса фотона кот. равна .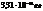

Масса фотона:m=(hν)/c² откуда частота колебаний световой волны:ν=(mc²)/h , ν=(3.31*10^-36*(3*10⁸)²)/6.62*10^-34=4.5*10¹⁴ Гц

46. Определить импульс фотона излучения с частотой 3×10¹⁵ Гц.

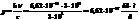
Монохроматический пучок света с длиной волны 490 нм, падая по нормали к поверхности, производит световое давление 4,9 мкПа. Какое число фотонов падает в единицу времени на единицу площади этой поверхности? Коэффициент отражения света 0,25.

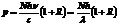; N= =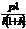

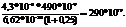
Плоская вольфрамовая пластинка освещается светом длиной волны 0,2 мкм. Найти напряженность однородного задерживающего поля вне пластинки, если фотоэлектрон может удалиться от нее на расстояние 4 см. Работа выхода электронов из вольфрама 4,5 эВ.

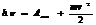, т.к. , ,

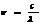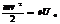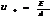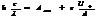а => тогда 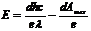. Ответ в В/м или Н/Кл

19. На фотоэлемент с катодом из лития падает свет с длиной волны 200 нм. Найти наименьшее значение задерживающей разности потенциалов, которую нужно приложить к фотоэлементу, чтобы прекратить фототок. =>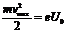

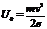
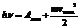, отсюда 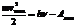, для лития А_вых=2,38 эВ.

Постулаты Бора.

1) В атоме существуют стационарные круговые орбиты, по которым электрон движется без излучения. Стационарными орбитами будут те, для которых момент количества движения 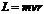электрона может принимать значения, кратные 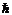. То есть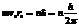

2) При переходе атома из состояния с энергией 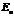в состояние с энергией 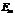( 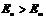) излучается один фотон (квант), энергия которого равна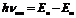

Правило квантования орбит.

Правило квантования, приводящее к правильным, согласующимся с опытом значениям энергий стационарных состояний атома водорода, было угадано Бором. Бор предположил, что выполняется следующее соотношение между скоростью движения электрона и радиусом орбиты: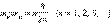

Здесь m – масса электрона, v– его скорость, rn – радиус стационарной круговой орбиты. Правило квантования Бора позволяет вычислить радиусы стационарных орбит электрона в атоме водорода и определить значения энергий.

Найти длину волны фотона при переходе электрона из состояния с энергией (–5 эВ) в состояние с энергией (–9 эВ).

2-ой постулат Бора 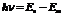, отсюда ,

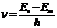так как 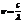, тогда 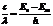, длина волны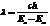

41. Энергия электрона в водородоподобном атоме определяется соотношением 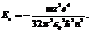Выразить через эти обозначения энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на первый.

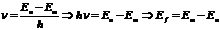
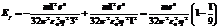подставить значения констант в уравнение. Ответ в Дж или в эВ.

42. Атом водорода в основном состоянии с энергией 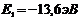поглотил квант света с длиной волны 121,5 нм. Определить энергию возбуждённого атома.

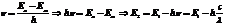
43. Энергия электрона в водородоподобном атоме определяется соотношением 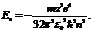Выразить через эти обозначения энергию фотона, который испускает ион гелия He⁺ при переходе со второго энергетического уровня на первый.

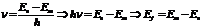
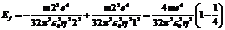подставить значения констант в уравнение. Ответ в Дж или в эВ.

44. На сколько изменится энергия электрона в атоме водорода при излучении атомом фотона с длиной волны ?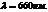

Согласно второму постулату Бора частота излучения, соответствующая переходу электрона с одной орбиты на другую, определяется формуло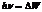й или 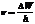- (1). С другой стороны 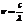- (2),

где с=3*10⁸ м/с – скорость света, 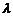-длина волны излученного атомом фотона. Приравнивая равные части уравнений (1) и (2). Получаем 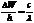, откуда изменение кинетической энергии электрона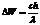

Опыт Дэвиссона и Джермера.

Физический эксперименты по дифракции электронов. Проводились исс