Частица в трехмерной потенциальной яме с абсолютно непроницаемыми стенками. Энергетический спектр частицы. Понятие о вырождении энергетических уровней.

Потенциальный ящик: G={(x,y,z):0<x<a1,0<y<a2,0<z<a3}. U(x,y,z)={0: (x,y,z)ÎG, ¥: (x,y,z)ÏG}. Будем искать волновую функцию в виде произведения: y(x,y,z)= y1(x) y2(y) y3(z)=>(1/y1(x))(d2y1(x)/dx2)+ (1/y2(y))(d2y2(y)/dy2)+(1/y3(z)) (d2y3(z)/dz2)=-2m0E/ħ2. Первое слагаемое в левой части зависит только от x, а второе - только отy. Поскольку их сумма равна постоянной величине, то это означает, что каждое из слагаемых также представляет собой постоянную величину. Получаем три одномерных уравнения: d2y1(x)/dx2+2m0E1y1(x)/ ħ2=0, d2y2(y)/dy2+2m0E2y2(y)/ ħ2=0, d2y3(z)/dz2+2m0E3y3(z)/ ħ2=0=> 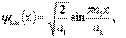аналогично для y2(y) и y3(z)=> 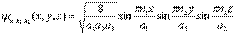, а её энергетический спектр 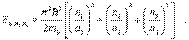Энергетический уровень, которому соответствует не одно, а несколько состояний частицы, называется вырожденным уровнем, а число соответствующих ему состояний называется кратностью вырождения или степенью вырождения уровня.

Движение микрочастицы в области одномерного потенциального порога. Надбарьерное отражение частицы в случае низкого порога.

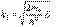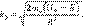Потенциальный порог: U(x)={0: x<0; U0,x>0}. Пусть E<U0. Обозначив и получим ур-ние Шредингера в виде d2y1(x)/dx2+k12y1=0 и d2y2(x)/dx2-k22y2=0. Решением уравнения являются: y1(x)=A1exp{ik1x}+ B1exp{-ik1x} и y2(x)=A2exp{k2x}+ B2exp{-k2x}. Поскольку волновая функция должна быть ограниченной, а первое слагаемое в волновой функции y2(x) при x, стремящемся к бесконечности, неограниченно возрастает, то необходимо потребовать A2=0. Из условий сшивки y1(0)= y2(0) и y1’(0)= y2’(0)=> A1­+B1=B2 и ik1A1­-ik1B1=-k2B2. A1=1=>B1=(k1-ik2)/(k1+ik2); B2=2k1/(k1+ik2).=>y1(x)=exp{ik1x}+(k1-ik2)/(k1+ik2)exp{-ik1x} и y2(x)= 2k1/(k1+ik2)exp{-k2x}. Коэф-т отражения R=|B1|2/|A1|2=1, коэф-т прохождения D=0. Пусть E>U0. Положим

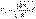и 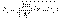=> d2y1(x)/dx2+k12y1=0 и d2y2(x)/dx2+k22y2=0=> y1(x)= A1exp{ik1x}+B1exp{-ik1x} и y2(x)=A2exp{ik2x}+ B2exp{-ik2x}. Поскольку отраженная волна в области II отсутствует, то B2 =0. Условие сшивки: A1­+B1=A2 и k1A1­-k1B1=k2B2. Полагая A1=1=> B1=(k1-k2)/(k1+k2); A2=2k1/(k1+k2)=> y1(x)=exp{ik1x}+(k1-k2)/(k1+k2)exp{-ik1x} и y2(x)= 2k1/(k1+ik2)exp{ik2x}. R=|B1|2/|A1|2, D=|A2|2/|A1|2.

16, 17.Представление физических величин операторами. Вычисление средних значений физических величин.

А) Оператор координаты. Действие сводится к умножению волновой функции на эту координату: x^{^}y=xy, y^y=yy, z^y=zy или x^=x…

б) Оператор проекций импульса. Выражаются с помощью операторов дифференцирования по соответствующим координатам: P^_x=(h/i)(¶/¶x), P^_y=(h/i)(¶/¶y), P^_z=(h/i)(¶/¶z),­­­­­­`p^={ P^_x, P^_y, P^_z}.

В) Оператор момента импульса:`

L=`r´`p, L_x=yp_z-zp_y; L_y=zp_y-xp_z; L_z=xp_y-yp_x;

L^_x=y^p^_z-z^p^_y=(h/i)(y¶/¶x-z¶/¶y).

Г) Оператор кинетической энергии. Определим T, пользуясь формулой Т=p²/2m, T^=p^²/2m=-h²/2m. Вычисление средних значений: L^y=Ly,<L>=òy*L^ydV, y(r)=Aexp(-r/a)

Условия возможности одновременного измерения разных величин. Соотношение неопределенностей Гейзенберга.

Гейзенберг предположил, что невозможно определить точно положение и импульс. Неопределенность положения х и р_х удовлетворяют соотношению

ìΔx·p_x≥ħ/2

íΔy·p_y≥ħ/2

îΔz·p_z≥ħ/2 Обозначив канонически сопряженные величины буквами А и В получим ΔА·ΔВ≥ħ/2. Производные неопределенностей значений двух сопряженных переменных не может быть по порядку величина меньше постоянной Планка ħ. Энергия и время тоже канонически сопряженные величины ΔЕ·Δt.≥ħ