Окислительно-восстановительные, или редокси-электроды

Любая электродная реакция связана с изменением окислительно-восстановительного состояния участвующих в ней веществ, и в этом смысле все электроды представляют собой редокси-системы. Однако термин окислительно-восстановительные, или редокси-электроды, употребляется обычно в тех случаях, когда в реакции не участвуют непосредственно металлы или газы. Металл в редокси-электроде, обмениваясь электронами с участниками окислительно-восстановительной реакции, принимает потенциал, отвечающий установившемуся редокси-равновесию. К металлическому проводнику предъявляются здесь те же требования, что и в случае газовых электродов.

Следует различать простые и сложные редокси-электроды. В первом случае электродная реакция сводится к перемене валентности ионов без изменения их состава, например

Fe³⁺ + e = Fe²⁺

Tl³⁺ + 2e = Tl⁺

MnO₄^– + e = MnO₄^2–

Если обозначить окисленные ионы Ox, а восстановленные Red, то все написанные выше реакции можно выразить одним общим уравнением

Ox + ne = Red .

Простой редокси-электрод записывается в виде схемы

Red, Ox êPt ,

а его потенциал дается уравнением

E_Red,Ox = E^o_Red,Ox + 2,303 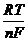lg .

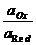Как видно, потенциал простого редокси-электрода определяется отношением активностей ионов в двух различных степенях окисления. Если элемент образует ионы нескольких валентностей, то ему будет отвечать столько редокси-электродов, сколько можно получить попарных сочетаний (три валентности - три различных редокси-электрода).

Потенциалы простых редокси-электродов можно легко связать с потенциалами соответствующих электродов первого рода. Пусть, например, металл М способен существовать в растворе в виде ионов высшей валентности М^h и низшей валентности Mⁿ. Для него возможны два электрода первого рода M^h êM и Mⁿ êM и один редокси-электрод Mⁿ, M^h êM , стандартные потенциалы которых соответственно равны 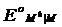, 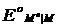и 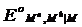. Связь между этими величинами можно найти, проведя мысленно процесс электрохимического растворения металла М с получением ионов высшей валентности M^h либо непосредственно, либо через промежуточное образование ионов низшей валентности Mⁿ. Предполагается, что процесс растворения протекает обратимо и изотермически в бесконечно большом объеме раствора, в котором активности ионов каждого сорта равны 1. Этот процесс можно представить в виде следующего простого цикла:

- hFE^o_h

M ----® M^h

- nFE^o_n æ ä - (h-n)FE^o_n,h

Mⁿ

Из цикла следует: hE^o_h = nE^o_n + (h - n)E^o_n,h .

Это уравнение известно как правило Лютера; по нему можно рассчитать стандартный потенциал любого из трех электродов, если известны значения стандартных потенциалов двух других электродов. Уравнение применяется в тех случаях, когда непосредственное определение одного из потенциалов или затруднительно, или невозможно. Так, например, потенциал электрода первого рода Fe³⁺ | Fe , измерить который непосредственно не удается из-за неустойчивости в этих условиях ионов Fe³⁺, можно найти из доступных прямому измерению стандартных потенциалов электрода первого рода Fe²⁺ | Fe и простого редокси-электрода Fe²⁺, Fe³⁺| Fe:

= + .

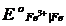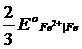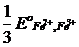В сложных редокси-электродах реакция протекает с изменением валентности реагирующих частиц и их состава. В реакциях такого рода участвуют обычно ионы водорода и молекулы воды; участие молекул воды не сказывается на характере уравнений для электродного потенциала, так как активность воды в ходе реакции (за исключением очень концентрированных растворов) остается постоянной. Схему сложного редокси-электрода можно записать следующим образом:

Red, Ox, H⁺ | Pt .

Таким образом, потенциал сложного редокси-электрода является функцией не только активностей окисленных и восстановленных частиц, но и активности водородных ионов, и, следовательно, сложные редокси-электроды можно использовать как индикаторные электроды при измерении рН. Для этой цели часто применяют электрод, обратимый по отношению к системе хинон-гидрохинон. Для системы хинон-гидрохинон (х, гх) с реакцией

С₆Н₄О₂ + 2Н⁺ + 2е = С₆Н₄(ОН)₂

потенциалу электрода отвечает уравнение

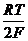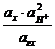E_{х, гх} = E^о_{х, гх} + 2,303 lg = E^о_{х, гх} + 2,303 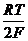lg +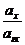

+ 2,303 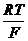lg .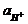

В раствор, рН которого хотят измерить, вводят эквимолярную смесь хинона и гидрохинона. Если считать, что отношение концентраций равно отношению активностей

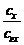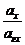= = 1 ,

то уравнение упрощается до

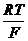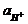E_{х, гх} = E^о_{х, гх} + 2,303 lg = E^о_{х, гх} - 2,303 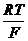рН

и потенциал такого электрода, обычно называемого хингидронным, будет определяться непосредственно значением рН раствора. При 25^оС E^о_{х, гх} = 0,6992 В; температурная зависимость E^о_{х, гх} хорошо изучена. Хингидронный электрод легко приготовляется и удобен в работе. Хингидронным электродом нельзя пользоваться в щелочных растворах (гидрохинон - слабая кислота, в щелочной среде он сильно диссоциирует и концентрация его в насыщенном растворе не является постоянной), а также в присутствии сильных окислителей или восстановителей.

Что надо знать железно!!!, чтобы не получить 3(три)!!!

1. Предмет термодинамики. Термодинамическая система . . .

Основополагающий вопрос во всей термодинамике, включены только существенные определения и формулы, знать все, можно забыть только вывод для адиабатического процесса, но формулу для работы знать.

2. Энтропия в случае равновесных и неравновесных процессов . . .

– выражение для КПД цикла Карно

– что такое приведенная теплота

– неравенство Клаузиуса

– условие изолированности системы (U, V = const) и вопрос об энтропии как критерии направления процесса и равновесия в изолированной системе

3. Растворы . . .

– определение, что такое растворы; каковы основные параметры состояния растворов; что растворы образуются самопроизвольно и DG < 0

– что такое химический потенциал (определение; написать выражение для химического потенциала как частной производной четырех термодинамических потенциалов по массе i –го компонента); абсолютное значение химического потенциала не можем ни определить на опыте, ни рассчитать!

– закон Рауля (формулировка, математическое выражение) и какие растворы называют идеальными

– закон Генри, объединенный закон Рауля – Генри и область его применимости

– какие растворы называют предельно разбавленными

– чем вызваны положительные и отрицательные отклонения от закона Рауля, нарисовать графики для тех и других

4. Химическое равновесие . . .

– что такое химическая переменная (c – «хи»)

– условие химического равновесия (в общей форме)

– уметь написать ЗДМ (закон действующих масс), а именно выражение для константы равновесия, для любой реакции, через давления и концентрации (с, N); помнить про К_Р , К_С , К_N , какая между ними связь, какие из них зависят от общего давления, а какие – нет, и в каком случае все три константы совпадают по величине

– уметь написать уравнение изотермы химической реакции для изобарного и изохорного потенциала

– что такое стандартный изобарный потенциал реакции, для чего он применяется (можно оценить направление реакции и комбинировать равновесия – рассказать, как)

– что основной задачей химической термодинамики (для чего, собственно, в химии и нужна физическая дисциплина термодинамика) является теоретический расчет!!! (не проводить бесконечные опыты, а рассчитать) DG, и, следовательно, константы равновесия, и, следовательно, выхода продукта при любой температуре, чтобы определить оптимальные условия для проведения реакции в промышленных масштабах. А для этого надо знать: 1) стандартные теплоты образования всех участников реакции; 2) эмпирическую зависимость теплоемкости всех участников от Т; 3) стандартные абсолютные энтропии участников реакции S^o₂₉₈ . Чтобы рассчитать S^o₂₉₈ , опять-таки, надо знать С_Р = f(T) в широком интервале температур (от 70 К или ниже) и теплоты фазовых переходов. Когда эти данные есть, то точный расчет константы равновесия возможен (тупо интегрируем уравнение

DG_T^o = DH_T^o – TDS_T^o = DН^о₂₉₈ + 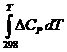– TDS^o₂₉₈ – T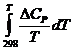

с учетом зависимости С_Р = f(T) либо используем метод Темкина – Шварцмана), а если нет (в большинстве случаев), то прибегают к приближенным методам – приближения Улиха.

5. Основной постулат химической кинетики , . .

Основополагающая лекция по кинетике. Желательно знать все, но обратить внимание на:

– формулировку основного постулата химической кинетики и характеристику входящих в него величин

– различие понятий «молекулярность» и «порядок реакции», что эти величины, как правило, не совпадают (указать, почему) и не связаны со стехиометрическими коэффициентами уравнения реакции; по уравнению реакции нельзя предсказать ни ее порядок, ни молекулярность, ни, тем более, механизм

– понятие элементарной реакции (это либо химическая реакция, протекающая в одну стадию – но таких реакций не более десятка во всей химии, либо стадия сложной реакции – параллельной, последовательной и др,), для нее совпадают молекулярность реакции, порядок реакции и сумма стехиометрических коэффициентов

– кинетическая классификация реакций

– для необратимой реакции любого порядка уметь написать: 1) дифференциальное уравнение скорости; 2) выражение для константы скорости с указанием ее размерности; 3) выражение для периода полураспада

6. Удельная и эквивалентная электропроводность . . .

– определение удельной и эквивалентной электропроводности, из размерность, зависимость от концентрации и разведения (для удельной объяснить, почему зависимость от концентрации проходит через максимум и для сильных, и для слабых электролитов)

– что такое абсолютная подвижность ионов, подвижность ионов (ионная электропроводность), предельная подвижность ионов – определение, размерность

– два закона Кольрауша для электропроводности

– формула Стокса, ее анализ: как зависит подвижность от размера иона и его заряда, чем эффективный диаметр иона отличается от кристаллохимического и почему катионы рубидия и цезия более подвижны, чем катионы лития

– механизм аномальной подвижности ионов гидроксония и гидроксила

7. Гальванические элементы. ЭДС. . .

– что такое гальванический элемент и что является его важнейшей характеристикой (ЭДС)

– понятия: правильно разомкнутый элемент, обратимый и необратимый элемент

– правильная запись гальванического элемента

– электродный потенциал: знать, что абсолютное значение потенциала отдельного электрода экспериментально определить невозможно и теоретически рассчитать (в настоящее время, при нашем уровне знаний) тоже нельзя. Выход: условная шкала потенциалов. Безупречно знать, потенциал какого электрода принят в настоящее время за условный нуль потенциалов, и что называется электродным потенциалом

– по какой причине и где возникает диффузионный потенциал и как его можно существенно уменьшить

– что такое стандартный электродный потенциал, от чего он зависит (1) от природы электрода; 2) от Т; 3) от давления, пусть очень незначительно), от концентрации раствора не зависит!

– представлять, пусть без формул и уравнений, для решения каких задач используют таблицу стандартных электродных потенциалов

8. Классификация электродов . . .

Очень важный вопрос, основополагающий в теории ЭДС и потенциалов

– знать, какой принцип лежит в основе классификации электродов

– для каждого типа электродов знать: 1) определение электрода; 2) схему электрода; 3) написать электродную реакцию; 4) написать выражение для потенциала электрода ипровести его анализ! (это самое главное); 5) примеры, применение электродов

– для электродов 2-го рода обязательно показать их обратимость и по отношению к аниону раствора, и по отношению к катиону электродного металла (т.е. показать связь между стандартными потенциалами электродов 1-го рода, 2-го рода и ПР)

– как итог, сделать вывод, какие электроды можно применять в качестве электродов сравнения и в качестве индикаторных электродов при определении рН раствора; указать их достоинства и недостатки