Влияние природы растворителя на электропроводность

Электропроводность растворов электролитов зависит в первую очередь от природы электролита и растворителя. При переходе от воды к другим растворителям изменяются величина электропроводности и, в меньшей степени, число переноса. Основными свойствами растворителя, обусловливающими характер изменения электропроводности, являются его вязкость и диэлектрическая проницаемость.

Повышение вязкости снижает электропроводность. Количественное выражение этого эффекта дается правилом Вальдена – Писаржевского:

l_оh_о = const

(l_о – мольная электропроводность электролита, экстраполированная до нулевой концентрации; h_о – вязкость чистого растворителя). Правило Вальдена – Писаржевского приближенно и оправдывается лишь для растворителей с близкими величинами диэлектрических проницаемостей.

Величина диэлектрической проницаемости растворителя влияет, во-первых, на абсолютную величину электропроводности (вспомним, что образование ионов в растворе в результате диссоциации происходит только в растворителях с высокой диэлектрической проницаемостью) и, во-вторых, заметно влияет на характер изменения электропроводности с концентрацией.

Зависимость пожвижности ионов от температуры

Предельная подвижность ионов, а также удельная электропроводность электролитов всегда увеличиваются с повышением температуры (в противоположность электропроводности металлов, которая уменьшается с повышением температуры). Температурный коэффициент подвижности оказывается довольно большим; при нагревании раствора на 1^oС подвижность, а следовательно, и электропроводность возрастают примерно на 2 %. Наибольший температурный коэффициент характерен для ионов с относительно малой подвижностью и наоборот. Наличие положительного температурного коэффициента подвижности ионов объясняется уменьшением вязкости с температурой.

Так как l_¥ = l^о₊ + l^о_– , то эквивалентная электропроводность при бесконечном разведении с температурой всегда возрастает.

При конечной концентрации связь l с подвижностью несколько сложнее. Для слабого электролита l = (l₊ + l_–)×a. Если с повышением температуры подвижности ионов возрастают, то степень диссоциации может и уменьшаться, поскольку диэлектрическая проницаемость раствора при нагревании уменьшается, то есть силы взаимодействия между ионами увеличиваются. Следовательно, кривая зависимости электропроводности от температуры может иметь максимум. Аналогичное явление наблюдается и в сильных электролитах.

Гальванические элементы. ЭДС. Связь ЭДС с константой равновесия реакции. Электродный потенциал. Диффузионный потенциал. Термодинамический вывод формулы Нернста для электродного потенциала. Стандартный электродный потенциал.

При прохождении электрического тока через электролит на поверхности электродов протекают электрохимические реакции. Протекание электрохимических реакций может порождаться внешним источником тока. Возможно и обратное явление: электрохимические реакции, протекающие на двух электродах, опущенных в электролит, порождают электрический ток, причем реакции идут только при замкнутой цепи (при прохождении тока).

Электрохимическим (или гальваническим) элементом называется устройство для получения электрического тока за счет электрохимических реакций. Простейший электрохимический элемент состоит из двух металлических электродов (проводников первого рода), опущенных в электролит (проводник второго рода) и соединенных между собой металлическим контактом. Несколько электрохимических элементов, соединенных последовательно, образуют электрохимическую цепь.

Важнейшей количественной характеристикой электрохимического элемента является электродвижущая сила (ЭДС, Е), которая равна разности потенциалов правильно разомкнутого элемента (такого, у которого к конечным электродам элемента присоединены проводники первого рода из одного и того же материала).

Если при прохождении электрического тока в разных направлениях на поверхности электрода протекает одна и та же реакция, но в противоположных направлениях, то такие электроды, а также элемент или цепь, составленные из них, называются обратимыми. ЭДС обратимых элементов является их термодинамическим свойством, т.е. зависит только от Т, Р, природы веществ, составляющих электроды и растворы, и концентрации этих растворов. Пример обратимого элемента - элемент Даниэля-Якоби:

(-) Cu çZn çZnSO₄ ççCuSO₄ çCu (+)

в котором каждый электрод обратим. При работе элемента идут следующие реакции: Zn ® Zn²⁺ + 2e , Cu²⁺ + 2e ® Cu. При пропускании тока бесконечно малой силы от внешнего источника на электродах протекают обратные реакции.

Пример необратимого элемента - элемент Вольта:

(-) Zn ç H₂SO₄ çCu (+)

При работе элемента протекают реакции: Zn ® Zn²⁺ + 2e , 2H⁺ + 2e ® H₂ . При пропускании тока от внешнего источника электродными реакциями будут: 2H⁺ + 2e ® H₂ , Cu ® Cu²⁺ + 2e .

ЭДС электрохимического элемента является величиной положительной, т.к. она соответствует определенному самопроизвольно протекающему процессу, дающему положительную работу. Обратному процессу, который не может протекать самостоятельно, отвечала бы отрицательная ЭДС. При составлении цепи электрохимических элементов процесс в одном из элементов можно направить так, чтобы он сопровождался затратой работы извне (несамопроизвольный процесс), используя для этого работу другого элемента цепи, в котором идет самопроизвольный процесс. Суммарная ЭДС любой цепи равна алгебраической сумме положительных и отрицательных величин. Поэтому очень важно при записи схемы цепи учитывать знаки ЭДС, пользуясь принятыми правилами.

ЭДС электрохимической цепи считается положительной, если при записи цепи правый электрод заряжен положительно относительно левого (катионы при работе цепи проходят в растворе от электрода, записанного слева, по направлению к электроду, записанному справа, и в этом же направлении движутся во внешней цепи электроны).

Пусть в электрохимической системе обратимо и изотермически протекает реакция:

n_AA + n_BB + ... ± nF Û n_LL + n_MM + ... ±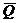

Свяжем ЭДС элемента с константой равновесия реакции, протекающей в элементе. Уравнение изотермы химической реакции:

-DG = RT lnK_a - RT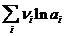

E = - 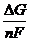= 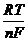lnK_a -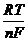

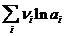
Первый член правой части уравнения при заданных Р, Т - величина постоянная, его можно обозначить через Е_о. Е_о - стандартная ЭДС элемента (электрохимической системы), т.е. ЭДС при всех a_i = 1.

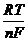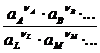Е = Е_о + ln = E_o + 2,303 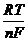lg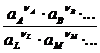

Т.о., ЭДС электрохимической системы является функцией активностей участников электрохимической реакции. Вышеприведенные уравнения дают возможность вычислить величины DG и К_а по экспериментальным значениям Е и, наоборот, рассчитывать Е, зная термодинамические характеристики химической реакции.

Электродный потенциал

Одна из основных особенностей электрохимической системы состоит в пространственном разделении участников протекающей в ней реакции. Общая реакция распадается здесь на две частные реакции, каждая из которых совершается на отдельном электроде. В соответствии с этим ЭДС электрохимической системы также должен представлять собой сумму двух электродных потенциалов: Е = Е₁ + Е₂.

Скачок потенциала на границе электрод-раствор (как и разность потенциалов между двумя точками, находящимися в различных фазах) экспериментально измерить невозможно. Величина такого скачка потенциала может быть рассчитана теоретически, но лишь в том случае, если точно известно строение границы раздела двух фаз. Структура границы между электродом и раствором изучена до сих пор недостаточно.

Экспериментально можно измерить лишь общее значение Е цепи, т.е. только сумму электродных потенциалов. Для устранения неопределённости величин Е необходимо ввести дополнительное условие - принять потенциал какого-либо электрода равным 0 и относить к нему значения потенциалов всех других электродов. В этом случае потенциалы электродов даются в некоторой условной шкале и их значения зависят от природы электрода, выбранного за основу шкалы.

Нернст предложил считать условным нулём потенциал водородного электрода при концентрации водородных ионов в растворе, равной 1, и давлении газообразного водорода 1 атм. Эта условная шкала потенциалов называется водородной шкалой. В настоящее время применяется условная водородная шкала, в которой при всех Т за ноль выбран потенциал стандартного водородного электрода. Она отличается от первоначальной водородной шкалы Нернста тем, что в ней вместо единичных концентраций и давления выбраны единичная активность и летучесть. Это условие позволяет определять потенциалы электродов в водородной шкале при любых Т, однако при каждой Т потенциал водородного электрода может быть иным, то есть условный нуль не будет одним и тем же при разных Т.

Т.о., электродным потенциалом электрода называется ЭДС элемента, составленного из этого электрода (справа) и стандартного водородного электрода (слева), например:

(+) Pt ïH₂ ç H⁺, aq çç Zn²⁺ ç Zn (-)

ЭДС этого элемента (Е_Zn2+çZn) отрицательна (-0,763 В при активности ионов цинка в растворе, равной 1, - это и есть стандартный электродный потенциал цинка). Чтобы найти электродный потенциал меди, нужно составить элемент:

(-) Pt ïH₂ ç H⁺, aq çç Cu²⁺ ç Cu (+)

Здесь ЭДС цепи (Е_Cu2+çCu) положительна (+0,337 В при активности ионов меди, равной 1, - стандартный электродный потенциал меди).

Диффузионный потенциал возникает на границе двух растворов, отличающихся друг от друга качественно и количественно. Причина его возникновения - неодинаковая подвижность ионов электролита и наличие градиента их концентрации.

На границе двух растворов имеется некоторый переходный слой, где состав меняется от раствора I до раствора II и от раствора II до раствора I; в этом переходном слое локализуется диффузионный потенциал. Ионы, обладающие большей подвижностью, диффундируют в более разбавленный раствор с большей скоростью, и поверхность соприкосновения двух растворов заряжается знаком этих ионов со стороны более разбавленного раствора и обратным знаком - со стороны концентрированного. Образуется диффузный двойной электрический слой с соответствующим скачком потенциала. Возникающая разность потенциалов будет ускорять движение медленно движущегося иона и замедлять движение быстро движущегося, пока не наступит стационарное состояние, при котором скорости диффундирующих ионов сравняются. Дальнейшее взаимное удаление зарядов прекращается; установившаяся в пограничном слое разность потенциалов и носит название диффузионного потенциала.

Диффузионный потенциал - неравновесный. Точно его рассчитать в общем случае невозможно.

При измерениях невысокой точности можно существенно снизить диффузионный потенциал на границе двух растворов, включив между ними солевой мостик - концентрированный электролит (насыщенный KCl или NH₄NO₃) с числами переноса ионов, близкими к 0,5. Резкое уменьшение диффузионного потенциала в этом случае связано с тем, что ионы концентрированного раствора проводят практически весь ток в зонах соприкосновения; один диффузионный потенциал заменяется при введении солевого мостика двумя потенциалами меньшей величины, часто противоположными по знаку. С этой же целью используется введение индифферентной соли во все растворы цепи.

Зависимость величины электродного потенциала от концентрации (активности) вещества в электролите может быть установлена методами термодинамики. На электроде Мⁿ⁺çМ с равновесным потенциалом Е протекает электрохимическая реакция: Мⁿ⁺, aq + ne = М .

Это - реакция дегидратации иона металла и включения его в кристаллическую решетку.

Для равновесного процесса при постоянных Р и Т убыль изобарного потенциала равна максимальной полезной работе А¢ - работе электрического тока:

А¢ = -DG = nFЕ .

При переходе 1 г-иона металла из раствора в электрод изменение изобарного потенциала равно разности химических потенциалов вещества в двух фазах: в растворе (m¢) и в электроде (m¢¢) : DG = m₊¢¢ - m₊¢ .

При Р,Т = const в электроде неизменного состава (чистый металл)

m₊¢¢ = m₊^о = const .

В растворе m₊¢ = m₊¢^о + RT ln a₊ .

m₊¢^о - химический потенциал иона в растворе в стандартном состоянии; эта величина при заданной Т постоянна.

DG = m₊^o - m₊¢^o - RT ln a₊ ,

Е = - (m₊^o - m₊¢^o)/nF + 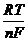ln a₊

Первый член правой части уравнения при постоянных Р и Т - величина постоянная (для металлического электрода эта величина практически не зависит от давления). Можно обозначить ее символом Е^о:

Е = Е^о + 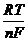ln a₊ (1)

В разбавленном растворе вместо активностей можно подставить концентрации (а₊ ® m₊ , c₊ , N₊) в зависимости от выбора меры концентрации и соответственно стандартного состояния для активности, например:

Е = Е^о + 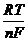ln m₊ (2)

Уравнение (2) было выведено Нернстом (1888) иным путем. Это уравнение, а также более общее уравнение (1) носит название уравнения электродного потенциала Нернста.

Е^о - это потенциал электрода относительно раствора с активностью соответствующих ионов, равной 1. Он называется стандартным электродным потенциалом и зависит от температуры.

Е = Е^о + 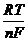ln a₊ = Е^о + 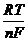ln m₊g¢₊ @ Е^о + 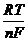ln m₊g¢_±

Подставляя значение F и переходя от натуральных логарифмов к десятичным, получаем для n = 1 и Т = 298 К:

Е = Е^о + 0,059 lg m₊g¢_±