Необратимые реакции второго порядка
Пример - реакция щелочного омыления сложного эфира
CH3COOC2H5 + NaOH ® CH3COONa + C2H5OH .
В общем виде реакция второго порядка описывается уравнением
А + В ® С + D + . . . .
Пусть в момент t = 0 имеется а моль вещества А и b моль вещества В. Пусть к моменту t прореагирует x моль вещества А, при этом (как видно из уравнения) прореагирует и x моль вещества В. Останутся не прореагировавшими (a - x) моль вещества А и (b - x) моль вещества В. Скорость реакции можно записать следующим образом:
- 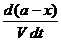 = k¢
= k¢ 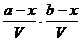 / × V и продифференцируем.
/ × V и продифференцируем.
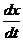 =
= 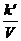 (а - х) (b - х) = k (а - х) (b - х)
(а - х) (b - х) = k (а - х) (b - х)
(если V = const, его можно ввести в константу: k¢ / V = k). Это уравнение и есть дифференциальное уравнение скорости необратимой реакции второго порядка. Интегрируем с учетом начальных условий:
k = 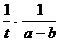 ln
ln 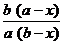 ; [k] = м3 /(с·моль) .
; [k] = м3 /(с·моль) .
Если а = b, то 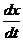 = k (a - x)2 ; k =
= k (a - x)2 ; k = 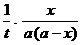 .
.
Когда х = а / 2 , t = t (времени полураспада): k = 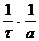 ; t =
; t = 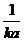 ,
,
то есть время полураспада для реакции второго порядка обратно пропорционально количеству исходного вещества. В случае, когда а ¹ b, периоды полураспада веществ А и В различны.
Необратимые реакции n-го порядка
В общем случае уравнение реакции n-го порядка имеет вид
А1 + А2 + . . . + Аn = А1¢ + А2¢ + . . . + Аn¢ .
Если реакция протекает при условии, что V = const и число молей каждого из веществ, участвующих в реакции, в исходный момент времени одинаково, то дифференциальное уравнение скорости будет иметь вид
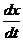 = k (a – x)n , где k =
= k (a – x)n , где k = 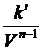 .
.
Проинтегрировав в пределах от 0 до t и от 0 до x, получим
k = 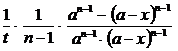 .
.
Подставив х = а/2 и t = t , получим t = 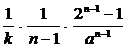 .
.
Видно, что t обратно пропорционально а n–1, n – порядок реакции. Следовательно, изучая экспериментально зависимость времени полураспада от количества исходного вещества, можно определить порядок реакции.
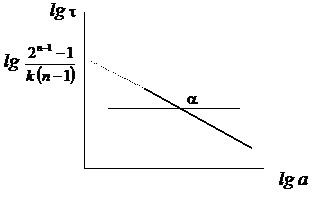 | lg t = lg 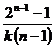 – (n – 1) lg a , tg a = 1 – n . Порядок реакции можно определить не только по времени полураспада, но и по времени превращения любой доли исходного вещества, например, 1/4, 1/3, 3/4 и т.д. – (n – 1) lg a , tg a = 1 – n . Порядок реакции можно определить не только по времени полураспада, но и по времени превращения любой доли исходного вещества, например, 1/4, 1/3, 3/4 и т.д. |
Реакции нулевого порядка
Такой порядок получается при постоянной скорости реакции, что возможно при поддержании постоянной концентрации исходных веществ. Нулевой порядок встречается главным образом в гетерогенных и фотохимических реакциях.
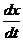 = k , dx = k dt , x = kt + const .
= k , dx = k dt , x = kt + const .
При t = 0 x = 0 Þ x = kt .
Удельная и эквивалентная электропроводность, ее зависимость от концентрации и температуры. Подвижность ионов, закон Кольрауша, формула Стокса. Аномальная подвижность ионов гидроксония и гидроксила (механизм).
Электропроводность К - величина, обратная электрическому сопротивлению R. Так как R = r 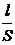 , то К =
, то К = 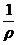 ×
× 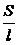 = k
= k 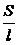

где r - удельное электрическое сопротивление; l - расстояние между электродами; S - площадь электрода; k - удельная электропроводность.
Удельная электропроводность k жидкости - это электропроводность одного кубического сантиметра раствора, заполняющего пространство между плоскими электродами одинаковой, очень большой площади, находящимися на расстоянии 1 см. Кубический сантиметр раствора должен находиться вдали от границ электрода. [k] = Ом–1× см–1.
Кривая зависимости удельной электропроводности растворов от концентрации обычно имеет максимум (четко выраженный для сильных электролитов и сглаженный для слабых). Наличие максимумов на кривых k - с можно объяснить следующим образом. Электропроводность растет пропорционально числу ионов, которое, в свою очередь, растет с концентрацией, но существуют и факторы противоположного действия. В концентрированных растворах сильных электролитов ионная атмосфера существенно уменьшает скорость движения ионов, и электропроводность падает. В слабых электролитах плотность ионной атмосферы мала и скорость движения ионов мало зависит от концентрации, однако с увеличением концентрации раствора заметно уменьшается степень диссоциации, что приводит к уменьшению концентрации ионов и падению электропроводности.
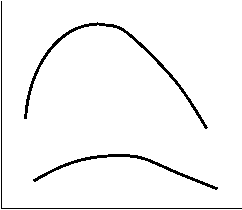 k сильный эл-т слабый эл-т С Зависимость удельной электропроводности от концентрации электролита k сильный эл-т слабый эл-т С Зависимость удельной электропроводности от концентрации электролита | 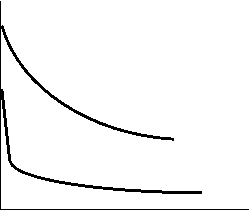 l сильный эл-т слабый эл-т С Зависимость эквивалентной электропроводности от концентрации электролита l сильный эл-т слабый эл-т С Зависимость эквивалентной электропроводности от концентрации электролита |
Удельная электропроводность зависит от температуры. Зависимость дается эмпирическим уравнением: kt = k18 × [1 + a (t - 18)]
a - температурный коэффициент электропроводности (a > 0); k18 (k25) - стандартное значение. Коэффициент a зависит от природы электролита. В случае слабых электролитов a больше, чем для сильных. Следует отметить, что температурные коэффициенты электропроводности водных растворов и вязкости воды близки по своей величине, но обратны по знаку. Это свидетельствует о том, что увеличение удельной электропроводности с ростом температуры связано, главным образом, с уменьшением вязкости раствора.
Эквивалентная электропроводность l [в см2/(г-экв×Ом)] - это электропроводность такого объема (j см3) раствора, в котором содержится 1 г-экв растворенного вещества; раствор заполняет пространство между плоскими электродами одинаковой, очень большой площади, находящимися на расстоянии 1 см.
Связь между k и l дается уравнениями
l = k× j ; l = 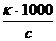
где величина j, равная 1000/с см3/г-экв, называется разведением.
Мольная электропроводность электролита m - это произведение эквивалентной электропроводности на число грамм-эквивалентов в 1 моль диссоциирующего вещества.
 l сильный эл-т слабый эл-т l сильный эл-т слабый эл-т 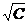 | 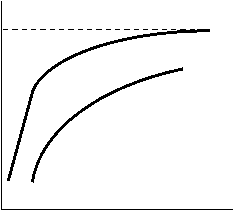 l сильный эл-т l¥ слабый эл-т j l сильный эл-т l¥ слабый эл-т j |
Зависимость эквивалентной электропроводности от концентрации:
1. Зависимость l - с : с увеличением с величина l уменьшается сначала резко, а затем более плавно.
2. Зависимость l - 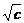 : для сильных электролитов в области малых концентраций соблюдается медленное линейное уменьшение l с увеличением
: для сильных электролитов в области малых концентраций соблюдается медленное линейное уменьшение l с увеличением 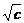 , что соответствует эмпирической формуле Кольрауша (закону квадратного корня):
, что соответствует эмпирической формуле Кольрауша (закону квадратного корня):
l = l¥ - А 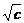
l¥ - предельная эквивалентная электропроводность при бесконечном разведении: с ® 0 , j ® ¥ . А – эмпирическая постоянная. При несколько более высоких концентрациях сильных электролитов лучшее согласие с опытом дает уравнение, известное под названием закона кубического корня:
l = l¥ - А 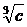
Для разбавленных растворов слабых электролитов вышеприведенные законы не соблюдаются.
3. Зависимость l - j : значение l сильных электролитов растет с увеличением j и асимптотически приближается к l¥ . Для слабых электролитов значение l также растет с увеличением j, но приближение к пределу и величину предела в большинстве случаев практически нельзя установить.
Подвижность ионов
Электропроводность электролитов зависит от следующих факторов: в первую очередь, от природы растворителя (вязкость, диэлектрическая проницаемость) и природы растворенного вещества (размера и заряда ионов), затем от напряженности поля, концентрации электролита, температуры и некоторых других. Для количественной характеристики влияния природы иона на величину электропроводности введены следующие понятия: абсолютная подвижность ионов, подвижность ионов (ионная электропроводность), предельная подвижность ионов.
Итак, скорости движения катионов u¢ (см/с) и анионов v¢ (см/с) зависят от природы ионов, напряженности электрического поля U/l , концентрации, Т, вязкости среды и т.п. Пусть все факторы постоянны, кроме напряженности электрического поля; можно считать, что скорость ионов пропорциональна приложенной силе – напряженности поля:
u¢ = u 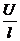 , v¢ = v
, v¢ = v 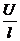
u, v - скорости ионов в стандартных условиях, т.е. при напряженности поля, равной 1 В/см; они называются абсолютными подвижностями ионов и измеряются в см2/(с×В).
u×F и v×F - это скорости движения ионов, выраженные в электростатических единицах; они называются ионными электропроводностями (или просто подвижностями ионов) :
u×F = l+ , v×F = l–
Для сильных электролитов: l = l+ + l–
Для слабых электролитов: с+ = с×a , с– = с×a , l = (l+ + l–)×a
При бесконечном разведении (j ® ¥ , a ® 1 , с+ = с– = с) :
l¥ = lо+ + lо–
- как для сильных, так и для слабых электролитов. Величины lо+ и lо– являются предельными электропроводностями (предельными подвижностями) ионов. Они равны эквивалентным электропроводностям катиона и аниона при бесконечном разведении и измеряются в тех же единицах, что и l и l¥ , т.е. в см2/(Ом×г-экв). Вышеприведенное уравнение является выражением закона Кольрауша: эквивалентная электропроводность при бесконечном разведении равна сумме предельных подвижностей ионов.
Т.о., для всех электролитов можно записать:
lс = aс×l¥ , aс = lс / l¥
l+ и l– зависят от концентрации (разведения), особенно для сильных электролитов; lо+ и lо– - табличные величины. Все эти величины относятся к 1 г-экв ионов.
Подвижность является важнейшей характеристикой ионов, отражающей их специфическое участие в электропроводности электролита. В водных растворах все ионы, за исключением ионов Н3О+ и ОН–, обладают подвижностями одного порядка; их lо составляют не более 80 см2/(Ом×г-экв) при 25оС; их абсолютные подвижности (u и v) равны нескольким см в час. Подвижности же ионов Н3О+ и ОН– составляют соответственно ~350 и ~200 см2/(Ом×г-экв).
Рассмотрим влияние природы иона (его радиуса и заряда) на величину подвижности иона. Движение иона можно уподобить движению макроскопического шарика в вязкой среде и применить в этом случае формулу Стокса:
u¢ = 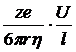
где е - заряд электрона; z - число элементарных зарядов иона; r - эффективный радиус иона (радиус гидратированного иона!), h - коэффициент вязкости; U/l - напряженность поля.
Движущую силу - напряженность поля U/l при вычислении абсолютных подвижностей принимаем равной единице. Следовательно, скорость движения ионов обратно пропорциональна их радиусу. Рассмотрим ряд Li+, Na+, K+. Так как в указанном ряду истинные радиусы ионов увеличиваются, то подвижности должны уменьшаться в той же последовательности. Однако в действительности это не так. Подвижности увеличиваются при переходе от Li+ к K+ почти в два раза. Из этого можно сделать заключение, что в растворе и ионной решётке ионы обладают разными радиусами. При этом чем меньше истинный (кристаллохимический) радиус иона, тем больше его эффективный радиус в электролите. Это явление можно объяснить тем, что в растворе ионы не свободны, а гидратированы. Тогда эффективный радиус движущегося в электрическом поле иона будет определяться в основном степенью его гидратации, то есть количеством связанных с ионом молекул воды.
Связь иона с молекулами растворителя ионно-дипольная, а так как напряжённость поля на поверхности иона лития гораздо больше, чем на поверхности иона калия, то степень гидратации иона лития больше степени гидратации иона калия, и эффективный радиус иона лития будет больше, чем у иона калия. Согласно формуле Стокса многозарядные ионы должны обладать большей подвижностью, чем однозарядные. Однако скорости движения многозарядных ионов ненамного превышают скорости движения однозарядных, что объясняется большей степенью их гидратации.
