Изменение внутренней энергии идеального газа пропорционально изменению температуры.
Изобарный процесс ( р = const )
dQP = dA + dU = р dV + dU ;
A = р (V2 - V1) = р DV ; A = рV2 - рV1 = nRT2 – nRT1 = nRDТ .
р 1 2 V1 V2 V График изобарного расширения (сжатия) идеального газа | На рис. приведен график изобарного расширения или сжатия. Работа равна площади прямоугольника. QP = DU + р DV ; Qp = QV + р DV ; Qp - QV = р DV. Разность теплот изобарного и изохорного процессов равна работе изобарного расширения или сжатия. |
dQp = dQV + р dV .
Продифференцируем это выражение по Т:
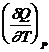 =
=  +
+  =
=  +
+ 
(так как рV = RT для 1 моля идеального газа).
Cр = СV + R ; Cр - CV = R- уравнение Майера.
Изотермический процесс ( T = const )
dU = CV dT = 0 .
Внутренняя энергия идеального газа в изотермическом процессе остается без изменения.
р 1 V1 V2 V График изотермического расширения (сжатия) идеального газа | рV = RT = const для изотермы. dA = р dV ; A =  = =  ; А = nRT ln ; А = nRT ln  = nRT ln = nRT ln  . dU = 0 , DU = 0 , Q = A. Теплота изотермического процесса равна работе процесса. . dU = 0 , DU = 0 , Q = A. Теплота изотермического процесса равна работе процесса. |
Закон Гей-Люссака – Джоуля: внутренняя энергия идеального газа не зависит от давления и объема, а зависит только от температуры.
Адиабатический процесс ( dQ = 0 , Q = 0 )
Это процесс, протекающий без теплообмена между системой и окружающей средой.
рdV + CV dT = 0 .
 dV + CV dT = 0 / : T ;
dV + CV dT = 0 / : T ;
R  + CV
+ CV 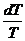 = 0 .
= 0 .
R = Cр - CV Þ (Cр - CV)  + CV
+ CV 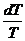 = 0 / : CV ;
= 0 / : CV ;
(  - 1)
- 1)  +
+ 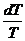 = 0 ,
= 0 ,  = g .
= g .
После интегрирования ln Vg-1 + ln T = const, ln TVg-1 = const.
TVg-1 = const¢. (1)
T =  ,
,  Vg-1 = const¢ ;
Vg-1 = const¢ ;
рVg = const¢¢ . (2)
Уравнения (1) и (2) - уравнения адиабаты (уравнения Пуассона).
Работа при адиабатическом процессе:
dA + CV dT = 0 , dA = - CV dT , A = -  = CV (T1 - T2).
= CV (T1 - T2).
A > 0 при расширении Þ Т падает при адиабатическом расширении, то есть работа адиабатического расширения совершается за счет уменьшения внутренней энергии. При адиабатическом сжатии U увеличивается, Т растет.
A = CV (T1 - T2) = CV (  -
-  ) =
) =  (р1V1 - р2V2) ;
(р1V1 - р2V2) ;
A =  (р1V1 - р2V2) =
(р1V1 - р2V2) =  (р1V1 - р2V2) =
(р1V1 - р2V2) =  (р1V1 - р2V2) .
(р1V1 - р2V2) .
 р изотерма адиабата V1 V2 V Графики изотермического и адиабатического процессов в идеальном газе р изотерма адиабата V1 V2 V Графики изотермического и адиабатического процессов в идеальном газе | Сравним: рVg = const¢¢ (адиабата) и рV = const (изотерма): р =  и р = и р =  . Адиабата идет круче, чем изотерма. . Адиабата идет круче, чем изотерма. |
Энтальпия
Энтальпия Н - это сумма внутренней энергии (U) и внешней (рV):
H = U + рV.
DH = DU + D(рV); при р = constDН = DU + рDV.
Изменение энтальпии в изобарном процессе включает в себя изменение внутренней и внешней энергии, причем изменение внешней энергии равно работе изобарного расширения (сжатия). U - функция состояния; р и V - параметры состояния, их изменение не зависит от пути процесса. Следовательно, энтальпия - также функция состояния, так как ее изменение не зависит от пути процесса.
Если процесс идет при р = const:
dQP = dU + р dV = dU + d (рV) = d (U + рV) = dH .
Тепло, передаваемое системе при р = const, расходуется на приращение энтальпии.
dQP = dH , QP = DH.
Теплота, поглощаемая при р = const, также не зависит от пути процесса.
Если процесс изобарно-изотермический, то DU = 0 и DH = р DV.
Cр = 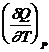 =
= 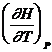 , dH = Cр dT,DH = Cр DT.
, dH = Cр dT,DH = Cр DT.
Введение энтальпии упрощает математическое выражение изобарного процесса. Кроме того, изменение Н может быть во многих случаях легко измерено, вследствие чего эта функция широко применяется при термодинамических исследованиях, особенно изобарных процессов.
Абсолютное значение энтальпии не может быть вычислено с помощью уравнений термодинамики, так как оно включает в себя абсолютную величину внутренней энергии.
2. Энтропия в случае равновесных и неравновесных процессов. Условия равновесия в изолированной системе
Для КПД цикла Карно было получено следующее уравнение:
h = 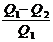 =
= 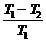 ; 1 -
; 1 - 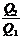 = 1 -
= 1 - 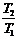
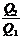 =
= 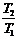 или
или 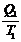 -
- 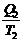 = 0
= 0
Отношение Q/Т - приведенная теплота. Вышеприведенная запись означает: алгебраическая сумма приведенных теплот по обратимому циклу Карно равна нулю.
 Понятие о б/м циклах Карно : 1. Бесконечно мала изотерма, конечна адиабата Понятие о б/м циклах Карно : 1. Бесконечно мала изотерма, конечна адиабата 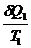 - - 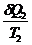 = 0 dQ/Т - элементарная приведенная теплота 2. Бесконечно мала адиабата, конечна изотерма = 0 dQ/Т - элементарная приведенная теплота 2. Бесконечно мала адиабата, конечна изотерма 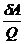 = = 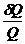 = = 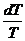 |  P dQ1, T1 Q , T Q - dQ, T - dT P dQ1, T1 Q , T Q - dQ, T - dT   dQ2, T2 V dQ2, T2 V |


