Угловые кинематические характеристики движения: Угол поворота, угловая скорость, угловое ускорение. Связь линейных и угловых кинематических характеристик.

При движении материальной точки по окружности постоянного радиуса (рис. 1.11) ее положение можно определить координатами x и y или углом поворота j – углом между радиус-вектором 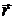, определяющим положение точки, и осью ОХ.

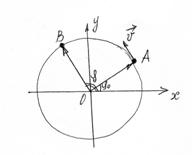
Рис. 1.11

Если рассматривать вращательное движение твердого тела, имеющего неподвижную ось вращения, то из рис.1.12 следует, что угол поворота радиусов-векторов, определяющих положение всех точек твердого тела, например, В и С, будет одним и тем же

Δj = j₂ – j₁, линейные же перемещения точек твердого тела будут различными ( 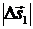¹ 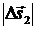). В связи с этим, если знать закон изменения угла j(t) для какой-то произвольной точки вращающегося твердого тела, то тем самым мы будем знать закон движение всех точек этого тела.

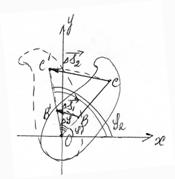
Рис. 1.12

При равномерном движении материальной точки по окружности а_t = 0, а_n ¹ 0, так как скорость изменяется только по направлению. Пусть за время Δt точка переместилась из положения А в В, радиус-вектор, определяющий положение точки, повернулся на Δj = j – j₀ (рис.1.13).

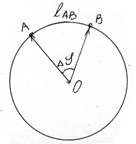
Рис. 1.13

Скорость изменения угла j есть угловая скорость w. При равномерном вращении

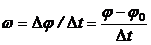(1.18)

Угловая скорость материальной точки равна отношению угла поворота радиуса-вектора, определяющего положение этой точки, к промежутку времени, за который этот поворот произошел.

Из формулы (1.18) следует, что

j = j₀ + wt, (1.19)

при t = 0, j = j₀.

По формуле (1.18) мы можем также определить среднюю угловую скорость.

Мгновенная угловая скорость определяется как предел отношения углового перемещения к промежутку времени, за которое это перемещение произошло при стремлении Δt к нулю, то есть равна первой производной от углового перемещения

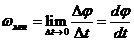(1.20)

Заметим, что движение по окружности может происходить как по часовой стрелке, так и против нее.

Угловая скорость – векторная величина, направленная вдоль оси вращения.

Направление угловой скорости определяется по правилу буравчика. Если вращать буравчик в направлении движения точки, то его поступательное движение укажет направление угловой скорости.

Если ось OZ направлена вверх и совпадает с осью вращения, то, как показано на рис. в случае вращения против часовой проекция угловой скорости положительна, а при вращении по часовой стрелке отрицательна.

Уравнение (1.19) можно переписать в виде: j = j ± wt, где w – модуль угловой скорости.

Заметим, что это выражение справедливо, если ось вращения постоянна и точка движется по окружности равномерно.

Угловое ускорение определяет скорость изменения угловой скорости

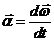
Угловое ускорение также векторная величина. При постоянной оси вращения направления векторов угловой скорости и ускорения совпадают, если угловая скорость увеличивается и направлены в противоположные стороны в случае ее уменьшения (см. рис. 1.14).