Оптическое излучение. фотометрические величины. фотометрические расчеты
Теоретические положения
Оптическое излучение - электромагнитное излучение, длина волн которого находится в диапазоне приблизительно от 1 нм до 1 мм. При этом по спектральному составу принято подразделять весь оптический диапазон на три области спектра: ультрафиолетовую - излучение с длиной волны от 1 нм до 0,38 мкм; видимую - излучение с длиной волны от 0,38 до 0,78 мкм и инфракрасную - излучение с длиной волны от 0,78 мкм до 1 мм [4].
Поток излучения [1,5]: 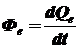 Вт, (1.1)
Вт, (1.1)
где: dQe - энергия, переносимая излучением за малый промежуток времени; dt - время переноса, существенно большее периода электромагнитных колебаний.
Облучённость в данной точке поверхности [1,5]:
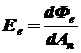 ,
, 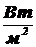 , (1.2)
, (1.2)
где dФe - поток излучения, падающий на малый участок поверхности, содержащий данную точку; dAп - площадь участка.
Сила излучения в данном направлении [1,5]:
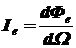 ,
,  , (1.3)
, (1.3)
где dФe - поток излучения, распространяющийся в малом телесном угле, содержащем данное направление; dΩ - величина телесного угла.
Энергетическая светимость данной точки поверхности [1,5]:
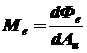 ,
, 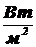 , (1.4)
, (1.4)
где dФe - поток излучения, испускаемый с малого участка поверхности, содержащего данную точку;dAи - площадь участка.
Энергетическая яркость данной точки поверхности в данном направлении [1,5]:
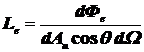 ,
, 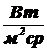 , (1.5)
, (1.5)
где dФe - поток излучения, распространяющийся с малого участка излучающей поверхности, содержащего данную точку, в малом телесном угле, содержащем данное направление; dAи- площадь участка; dW - величина телесного угла;q - угол между нормалью поверхности и направлением распространения излучения.
Поток излучения для любого участка спектра от l1 до lk [1]:
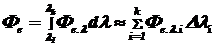 , (1.6)
, (1.6)
где 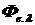 - СППИ;
- СППИ; 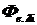 - средняя СППИ на малом спектральном интервале
- средняя СППИ на малом спектральном интервале 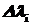 .
.
Связь фотонных и энергетических ФМВ:
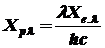 ; (1.7)
; (1.7)
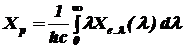 ; (1.8)
; (1.8)
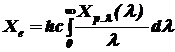 , (1.9)
, (1.9)
где Xp , Xe - соответственно фотонная и энергетическая ФМВ; Xe.l , Xp.l - спектральные плотности соответственно энергетической и фотонной ФМВ; Xe.l(l), Xp.l(l) - спектральные распределения соответственно энергетической и фотонной ФМВ; h- постоянная Планка (см. табл. 1); с - скорость распространения электромагнитного излучения в вакууме (см. табл. 1).
Световая ФМВ [2]: 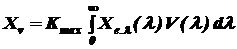 , (1.10)
, (1.10)
где Kmax - максимальная спектральная световая эффективность монохроматического излучения для дневного зрения (см. табл. 1); Xe.l(l) - спектральное распределение энергетической ФМВ; V(l) - относительная спектральная световая эффективность монохроматического излучения для дневного зрения (см. табл. 2).
Связь энергетических и световых ФМВ [8]:
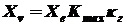 , (1.11)
, (1.11)
где kг - коэффициент использования излучения глазом (см. табл. 3):
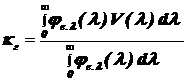 , (1.12)
, (1.12)
je.l(l) - относительное спектральное распределение потока излучения.
Шкала звёздных величин [16]:
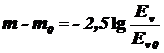 , (1.13)
, (1.13)
где m,m0 - звёздные величины двух звёзд; Ev , Ev.0 - освещённости, создаваемые этими звёздами. Если Ev.0 = 1 лк, то на границе земной атмосферы m0к = -13,89, а на уровне моря m0з = -14,2.
Коэффициент пропускания [9,1]:
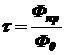 , (1.14)
, (1.14)
где Фпр - прошедший поток; Ф0 - падающий поток.
Коэффициент отражения [9,1]:
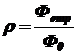 , (1.15)
, (1.15)
где Фотр - отражённый поток.
Коэффициент поглощения [9,1]:
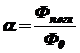 , (1.16)
, (1.16)
где Фпогл - поглощённый поток.
Энергетическая светимость облучаемой поверхности, создаваемая отражённым излучением:
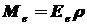 , (1.17)
, (1.17)
где Ee - облучённость поверхности; r - коэффициент отражения.
Облучённость, создаваемая точечным источником на поверхности, на которую излучение падает под углом [5]:
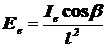 , (1.18)
, (1.18)
гдеIe - сила излучения источника; b - угол между нормалью поверхности и падающим излучением; l- расстояние от источника до поверхности.
Облучённость, создаваемая удалённым источником:
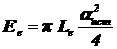 , (1.19)
, (1.19)
где Le - энергетическая яркость источника; aист - угловой размер источника.
Поток излучения, поступающий с излучающей поверхности источника на удалённую облучаемую поверхность [1,5]:
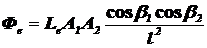 , (1.20)
, (1.20)
где Le - энергетическая яркость излучающей поверхности источника; A1, A2 - площади излучающей и облучаемой поверхностей; b1, b2 - углы между направлением распространения излучения и нормалями соответственно излучающей и облучаемой поверхностей; l - расстояние между поверхностями.
Поток излучения, создаваемый объективом в плоскости изображений при малом переднем апертурном угле [6]:
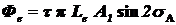 , (1.21)
, (1.21)
где t - коэффициент пропускания объектива; Le- энергетическая яркость источника; A1 - площадь излучающей поверхности; sA - передний апертурный угол объектива.
Поток излучения, создаваемый коллиматором в фокальной плоскости приёмного объектива при малом угле расходимости, постоянной силе излучения в пределах этого угла и диаметре приёмного объектива, меньшем диаметра объектива коллиматора [6]:
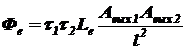 , (1.22)
, (1.22)
где t1, t2 - коэффициенты пропускания объектива коллиматора и приёмного объектива; Le - энергетическая яркость источника, расположенного в фокальной плоскости объектива коллиматора; Aвых.1, Aвых.2 - площади выходного и входного зрачков объектива коллиматора и приёмного объектива; l - расстояние между объективами. Линейное увеличение оптической системы [5]:
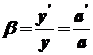 , (1.23)
, (1.23)
где y, y' - линейные размеры соответственно предмета и изображения; a, a' - расстояния от соответствующих главных плоскостей оптической системы до предмета и изображения.
Линейное увеличение оптической системы с предметом в фокальной плоскости одного объектива и изображением в фокальной плоскости второго объектива [7]:
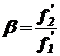 , (1.24)
, (1.24)
где f'1, f'2 - фокусные расстояния первого и второго объективов.
Видимое (угловое) увеличение телескопической системы [7]:
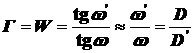 , (1.25)
, (1.25)
где w, w' - угловое поле в пространстве предметов и пространстве изображений; D, D'- диаметры входного и выходного зрачков системы.
Примеры решения задач
Задача 1.2.1
Вычислить монохроматические световые потоки 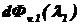 ,
, 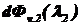 ,
, 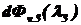 источника излучения с линейчатым спектром на длинах волн
источника излучения с линейчатым спектром на длинах волн 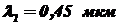 ,
, 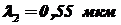 ,
, 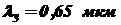 , если каждый из соответствующих потоков излучения равен 2 Вт.
, если каждый из соответствующих потоков излучения равен 2 Вт.
Дано:
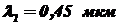 ,
, 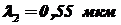 ,
, 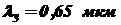 ,
,
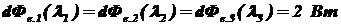 .
.
Определить: 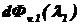 ,
, 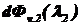 ,
, 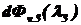 .
.
Решение:
Монохроматический поток излучения и монохроматический световой поток связаны соотношением, полученным из (1.10):
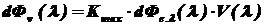 .
.
По табл. 1 и табл. 2 найдем: 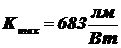 ,
,
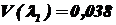 при
при 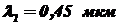 ;
;
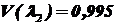 при
при 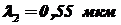 и
и
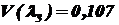 при
при 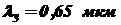 .
.
Тогда световые потоки будут равны:
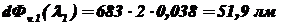 ;
;
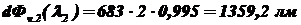 ;
;
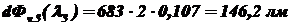 .
.
Ответ:
Монохроматические световые потоки на указанных длинах волн будут соответственно равны:
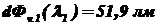 ;
; 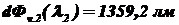 ;
; 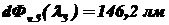 .
.
Задача 1.2.2
Найти порог чувствительности глаза, различающего с поверхности Земли звезду 5-ой звездной величины, если диаметр зрачка глаза 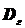 равен 5 мм.
равен 5 мм.
Дано:m = 5,
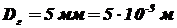 .
.
Определить: 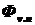 .
.
Решение:
Из выражения (1.13) найдем освещённость 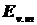 поверхности Земли, создаваемую звездой m-ой величины влюксах:
поверхности Земли, создаваемую звездой m-ой величины влюксах:
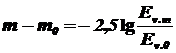 ,
,
где 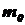 = -14,2 и
= -14,2 и 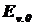 = 1лк,
= 1лк, 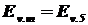 - освещённость, создаваемая звездой величины m = 5.
- освещённость, создаваемая звездой величины m = 5.
Тогда:
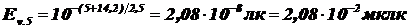 .
.
Порог чувствительности глаза есть минимальный световой поток 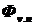 , падающий на зрачок глаза, который человек может различить. Определим его из выражения (1.2):
, падающий на зрачок глаза, который человек может различить. Определим его из выражения (1.2):
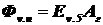 ,
,
где 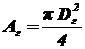 - площадь зрачка глаза.
- площадь зрачка глаза.
Тогда:
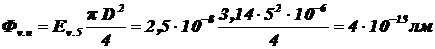 .
.
Ответ:
Порог чувствительности глаза 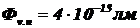 .
.
Задача 1.2.3
Поток излучения 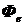 от источника типа ЧТ в форме отверстия площадью
от источника типа ЧТ в форме отверстия площадью 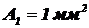 с энергетической светимостью
с энергетической светимостью 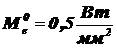 падает нормально на плоскость площадью
падает нормально на плоскость площадью 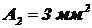 , находящуюся на расстоянии l = 1 м.
, находящуюся на расстоянии l = 1 м.
Найти 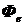 , если плоскость отверстия и облучаемая плоскость параллельны.
, если плоскость отверстия и облучаемая плоскость параллельны.
Указание: воспользоваться следствием из закона Ламберта.
Дано: 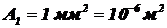 ,
, 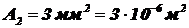 , l = 1 м,
, l = 1 м, 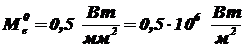 .
.
Определить: 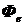 .
.
Решение:
ЧТ - ламбертовский излучатель, поэтому справедливо следствие из закона Ламберта (2.10): 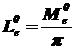 .
.
Поток излучения, падающий с излучающей поверхности на удаленную облучаемую поверхность по формуле (1.20) равен:
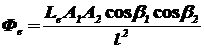 .
.
Так как поверхности параллельны, а поток падает нормально, то 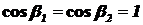 . Следовательно, поток излучения будет равен:
. Следовательно, поток излучения будет равен:
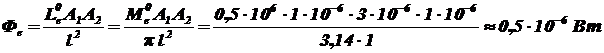
Ответ:
Поток излучения 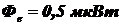 .
.
Задача 1.2.4
Вычислить поток излучения 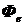 , падающий на плоскость площадью
, падающий на плоскость площадью 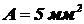 , расположенную на расстоянии 2 м от точечного источника, если его сила излучения равна
, расположенную на расстоянии 2 м от точечного источника, если его сила излучения равна 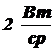 , а угол падения излучения на плоскость составляет 30°.
, а угол падения излучения на плоскость составляет 30°.
Дано: 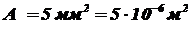 ,
,
l = 2 м,
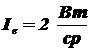 ,
,
β = 30°
Определить: 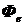
Решение:
По формуле (1.2) облученность в данной точке поверхности равна 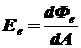 . По формуле (1.18) облученность, создаваемая точечным источником на поверхности, на которую излучение падает под углом β, равна:
. По формуле (1.18) облученность, создаваемая точечным источником на поверхности, на которую излучение падает под углом β, равна: 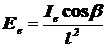 .
.
Тогда поток излучения, падающий на поверхность, будет определяться выражением:
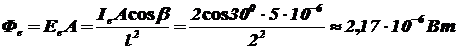 .
.
Ответ:
Поток излучения, падающий на площадку, равен 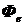 = 2,17 мкВт.
= 2,17 мкВт.
Задача 1.2.5
Найти поток излучения и облученность, создаваемую этим потоком на плоскости площадью 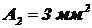 , находящейся на расстоянии l = 1 мот излучателя площадью
, находящейся на расстоянии l = 1 мот излучателя площадью 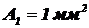 с одинаковой во всех направлениях энергетической яркостью
с одинаковой во всех направлениях энергетической яркостью 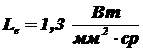 . Поверхность излучателя параллельна поверхности площадки и перпендикулярна линии, их соединяющей.
. Поверхность излучателя параллельна поверхности площадки и перпендикулярна линии, их соединяющей.
Дано: 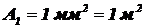 ,
, 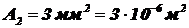 ,
,
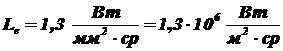 , l = 1 м.
, l = 1 м.
Определить: 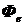 ,
, 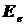 .
.
Решение:
Поток излучения, падающий с излучающей поверхности на удаленную облучаемую поверхность по формуле (1.20) равен:
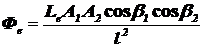 .
.
Так как поверхности излучателя и облучаемой площадки параллельны, а поток падает нормально к последней, то 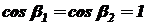 . Следовательно, поток излучения будет равен:
. Следовательно, поток излучения будет равен:
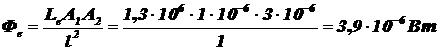 .
.
Облучённость равномерно облучаемой поверхности согласно формуле (1.2) равна:
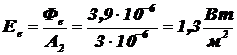 .
.
Ответ: Поток излучения и облученностьна плоскости соответственно равны: 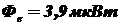 и
и 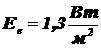 .
.
Задача 1.2.6
На высоте 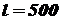 км вращается спутник диаметром 1 м (рис.1.2.1) Коэффициент отражения спутника
км вращается спутник диаметром 1 м (рис.1.2.1) Коэффициент отражения спутника 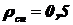 . Определить звёздную величину спутника.
. Определить звёздную величину спутника.
Яркость Солнца 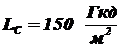 . Угловой размер Солнца
. Угловой размер Солнца 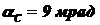 .
.
Указания: 1) Поглощением в атмосфере пренебречь.
2) Воспользоваться следствием из закона Ламберта.
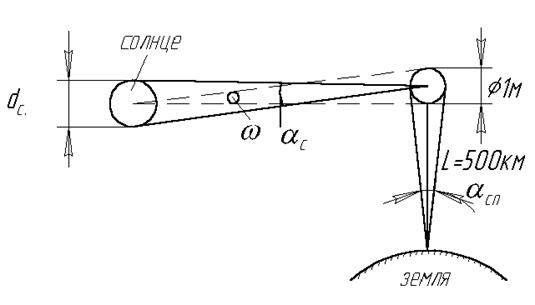 |
Рисунок 1.2.1
Дано: 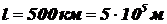 ,
, 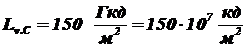 ,
,
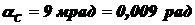 ,
, 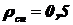 .
.
Определить: mсп
Решение:
1) По формуле (1.20) определяем освещённость спутника от Солнца:
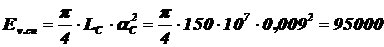 лк
лк
2) По формулам (1.17) и (2.4) определяемсветимость и яркость спутника:
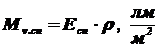 ,
,
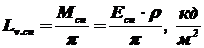 .
.
3) Рассчитываем освещённость Земли спутником, освещаемым Солнцем,по формуле (1.20):
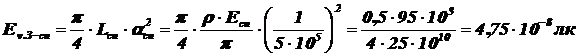 .
.
4) По формуле (1.13) определяемзвёздную величину спутника:
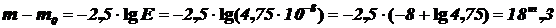 .
.
Откуда:
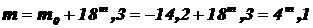
Ответ: Спутник является 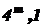 звёздной величиной.
звёздной величиной.
Комментарий к ответу: Поскольку невооружённый глаз различает пятую звёздную величину 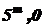 , глаз увидит спутник.
, глаз увидит спутник.
Задача 1.2.7
Имеется лампа накаливания с яркостью нити 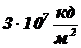 и площадью нити
и площадью нити 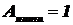 см2. Найти дистанцию
см2. Найти дистанцию 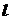 , на которой будет видна нить простым глазом в космосе при условии, что пороговая освещённость глаза
, на которой будет видна нить простым глазом в космосе при условии, что пороговая освещённость глаза 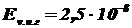 лк. Диаметр зрачка глаза
лк. Диаметр зрачка глаза 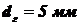 .
.
Найти также пороговый световой поток для глаза 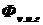 .
.
Дано: 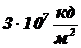 ,
, 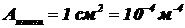 ,
, 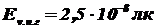 ,
, 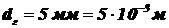 .
.
Определить: 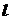 ,
, 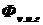 .
.
Решение:
Пороговая освещённость глаза может быть получена по формуле (1.19):
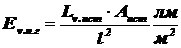 ,
,
Тогда:
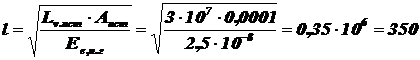 км.
км.
Выразим и определим пороговый световой поток для глаза через пороговую освещенность (см. формулу 1.2):
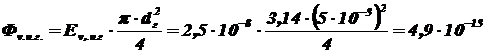 лм.
лм.
Ответ:
Нить видна глазом на расстоянии l = 350 км, а пороговый световой поток для глаза 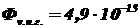 лм.
лм.
ЗАДАЧИ
1.3.1. Вычислить поток излучения на участке от 0,45 до 0,75 мкм, если спектральная плотность потока излучения (СППИ) постоянна и равна 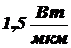 .
.
1.3.2. Найти световой поток гелий-неонового лазера, если его поток излучения равен 10 мВт, а длина волны излучения составляет 632,8 нм.
1.3.3. Найти монохроматическую облучённость в фотонах поверхности площадью 5 см2, если на неё падает монохроматический поток излучения 1 мВт с длиной волны 600 нм.
1.3.4. Источник с линейчатым спектром испускает монохроматическое излучение на длинах волн 200, 300, 2000 и 3000 нм с энергией излучения по 1020 фотонов в минуту. Определить монохромати-ческие потоки излучения, испускаемые источником в ультрафиолетовой, видимой и инфракрасной частях спектра.
1.3.5. Определить относительное изменение числа квантов, излучаемых в единицу времени, при изменении длины волны излучения от 1 мкм до 5 мкм, если мощность излучения на обеих длинах волн одинакова.
1.3.6. Найти световой поток, падающий на входной зрачок прибора площадью 100 см2 от звезды нулевой звёздной величины.
1.3.7. Найти световой поток, падающий на входной зрачок прибора диаметром 10 см от звезды пятой звёздной величины.
1.3.8. Найти энергетическую яркость диффузно отражающей по закону Ламберта поверхности площадью 5 мм2 с коэффициентом отражения 0,7, расположенной на расстоянии 2 м от точечного источника, если сила излучения источника равна 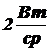 , а угол падения излучения на поверхность составляет 45°. Указание. Воспользоваться следствием из закона Ламберта.
, а угол падения излучения на поверхность составляет 45°. Указание. Воспользоваться следствием из закона Ламберта.
1.3.9. Энергетическая яркость источника равна 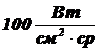 . Рассчитать поток излучения, падающий на ПОИ диаметром 1 см, находящийся на расстоянии 10 м от источника площадью 1 см2 и расположенный нормально к падающему излучению.
. Рассчитать поток излучения, падающий на ПОИ диаметром 1 см, находящийся на расстоянии 10 м от источника площадью 1 см2 и расположенный нормально к падающему излучению.
1.3.10. Найти поток излучения и облучённость, создаваемую этим потоком на плоскости, находящейся на расстоянии 1 м от излучателя площадью 1 мм2 с энергетической яркостью 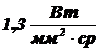 . Излучающая поверхность проектируется на плоскость объективом, имеющим диаметр 50 мм и коэффициент пропускания 1 и расположенным на расстоянии 150 мм от плоскости. Указание: Воспользоваться приближённым равенством: sin a » tg a при малых a.
. Излучающая поверхность проектируется на плоскость объективом, имеющим диаметр 50 мм и коэффициент пропускания 1 и расположенным на расстоянии 150 мм от плоскости. Указание: Воспользоваться приближённым равенством: sin a » tg a при малых a.
1.3.11. Найти поток излучения и облучённость, создаваемую этим потоком на плоскости, находящейся на расстоянии 1 м от излучателя площадью 1 мм2 с энергетической яркостью 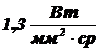 . Излучающая поверхность располагается в фокальной плоскости объектива с диаметром 60 мм и фокусным расстоянием 200 мм, а облучаемая плоскость - в фокальной плоскости объектива с диаметром 50 мм и фокусным расстоянием 150 мм. Коэффициенты пропускания объективов равны 1.
. Излучающая поверхность располагается в фокальной плоскости объектива с диаметром 60 мм и фокусным расстоянием 200 мм, а облучаемая плоскость - в фокальной плоскости объектива с диаметром 50 мм и фокусным расстоянием 150 мм. Коэффициенты пропускания объективов равны 1.
1.3.12. При серповидной форме Луны можно различить остальные её очертания, так как Луна освещается Землёй. Определить: 1) яркость ночной стороны Луны, освещённой Землёй; 2) яркость дневной стороны Луны, освещенной Солнцем, если коэффициент отражения Луны равен 0,07, Земли - 0,4, яркость Солнца составляет 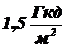 , угловой размер Земли со стороны Луны равен 34 мрад, угловой размер Солнца - 9 мрад. Указания: 1) расстояние от Земли до Солнца считать равным расстоянию от Луны до Солнца; 2) воспользоваться следствием из закона Ламберта.
, угловой размер Земли со стороны Луны равен 34 мрад, угловой размер Солнца - 9 мрад. Указания: 1) расстояние от Земли до Солнца считать равным расстоянию от Луны до Солнца; 2) воспользоваться следствием из закона Ламберта.
1.3.13. Луна облучается лазером с диаметром пучка 10 мм, углом расходимости 20' и мощностью в импульсе 109 Вт. Излучение лазера проходит через телескоп с диаметром входного зрачка 10 мм и выходного - 250 см. Расстояние от Земли до Луны равно 400000 км. Определить: 1) потоки излучения, отражённые от поверхности Луны и от уголкового отражателя, доставленного на неё, если коэффициент отражения Луны равен 0,07, а диаметр отражателя составляет 50 см; 2) потоки излучения, попадающие в зрачок телескопа (250 см) от Луны и от уголкового отражателя, если Луна отражает излучение по закону Ламберта, а расходимость пучка после уголкового отражателя равна 4". Указания: 1) потерями в атмосфере и телескопе пренебречь, 2) воспользоваться следствием из закона Ламберта.
1.3.14. На каком расстоянии видна простым глазом в космосе лампа накаливания с яркостью 50 Мкд/м2 и с площадью тела накала 2 см2, если пороговая освещённость для глаза равна 0,025 мклк.
1.3.15. Определить яркость источника площадью 1 мм2, который испускает внутри телесного угла в 0,03 ср световой поток 12 лм.
1.3.16. С левой стороны от фотометра на расстоянии 15 см находится эталонная лампа силой света 25 кд. Определить силу света испытуемой лампы, расположенной справа на расстоянии 45 см от фотометра, если обе половины фотометра освещены одинаково.
1.3.17. На мачте высотой 15 м подвешена электрическая лампа, создающая освещенность 1,63 лк на расстоянии 8 м от основания мачты. Определить силу света лампы.
1.3.18. Над центром круглой площадки висит электрическая лампочка. Освещенность в центре равна 40 лк, на краю 5 лк. Определить угол падения лучей на край площадки.
1.3.19. Два одинаковых точечных источника света установлены на высоте 6 м от земли и на расстоянии 16 м друг от друга. Определить полный световой поток, создаваемый каждым источником, если освещенность в точке, расположенной на земле посередине между источниками, составляет 7,2 лк.
1.3.20. Яркость Солнца составляет 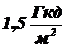 , диаметр 1,4 млн км. Определить силу света Солнца, наблюдаемую с Земли, и освещенность поверхности Земли, создаваемую нормально падающими солнечными лучами. Расстояние от Земли до Солнца равно
, диаметр 1,4 млн км. Определить силу света Солнца, наблюдаемую с Земли, и освещенность поверхности Земли, создаваемую нормально падающими солнечными лучами. Расстояние от Земли до Солнца равно 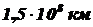 .
.
ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
Теоретические положения
Закон Стефана-Больцмана [1,5]:
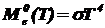 , (2.1)
, (2.1)
где Me0 - энергетическая светимость ЧТ; T - термодинамическая температура ЧТ; s - постоянная Стефана-Больцмана (см. табл. 1).
Закон Стефана-Больцмана для серых тел [1,5]:
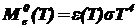 , (2.2)
, (2.2)
где Me - энергетическая светимость серого тела; e(T) - коэффициент теплового излучения серого тела:
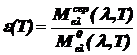 , (2.3)
, (2.3)
где 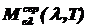 - СПЭС серого тела;
- СПЭС серого тела; 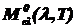 - СПЭС ЧТ.
- СПЭС ЧТ.
Закон смещения Вина для спектра длин волн [1,5]:
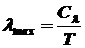 , (2.4)
, (2.4)
где lmax - длина волны, на которой СПЭС ЧТ в спектре длин волн максимальна; Cl - постоянная закона смещения в спектре длин волн (см. Табл. 1).
Закон смещения Вина для спектра частот [1,5]:
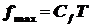 , (2.5)
, (2.5)
где fmax - частота излучения, на которой СПЭС ЧТ в спектре частот максимальна; Cf - постоянная закона смещения в спектре частот (см. Табл. 1).
Закон Планка в относительных величинах [1,5]:
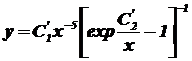 , (2.6)
, (2.6)
где: y - относительная СПЭС ЧТ; x - относительная длина волны; C1', C2' - постоянные закона Планка в относительных величинах (см. табл. 4);
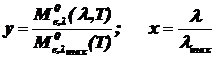 ,(2.7)
,(2.7)
где 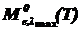 - максимальная СПЭС ЧТ.
- максимальная СПЭС ЧТ.
Второй закон Вина [1,5]:
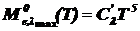 , (2.8)
, (2.8)
где Cl' - постоянная второго закона Вина (см. табл. 1).
Доля излучения ЧТ в интервале от l1 до l2 [8]:
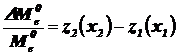 , (2.9)
, (2.9)
где x - относительная длина волны; 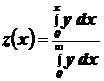 , (см. табл. 5).
, (см. табл. 5).
Следствие из закона Ламберта [1,5]:
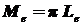 , (2.10)
, (2.10)
где Me - энергетическая светимость источника; Le- энергетическая яркость источника.
Связь истинной температуры с радиационной [1,5]:
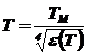 (2.11)
(2.11)
где T - истинная термодинамическая температура; ТM- радиационная температура; e(T) - коэффициент теплового излучения.
Связь яркостной температуры с истинной в видимой части спектра [1,5]:
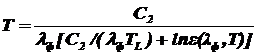 , (2.12)
, (2.12)
где ТL- яркостная температура; С2- вторая постоянная закона Планка (см. табл. 1); lф - длина волны излучения, пропускаемого оптическим фильтром.
Коэффициент теплового излучения металлов [10]:
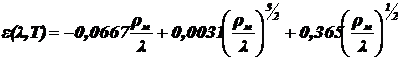 , (2.13)
, (2.13)
где rм - удельное сопротивление металла при данной температуре.
Зависимость удельного сопротивления металлов от температуры [10]:
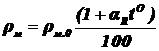 , Oм × м , (2.14)
, Oм × м , (2.14)
где rм.0 - удельное сопротивление металла при нормальной температуре (см. табл. 1); aR - температурный коэффициент сопротивления металла (см. табл. 1); t° - температура металла в градусах Цельсия.
Примеры решения задач
Задача 2.2.1
Для излучателя типа ЧТ с температурой 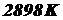 , площадью излучающей диафрагмы 1 см2 определить световой поток, светимость, и яркость.
, площадью излучающей диафрагмы 1 см2 определить световой поток, светимость, и яркость.
Дано: Тчт = 2897 К, 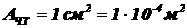 .
.
Определить: 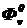 ,
, 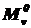 ,
, 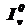 ,
, 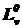 .
.
Решение:
1) По закону Стефана-Больцмана (2.1) найдем энергетическую светимость ЧТ: 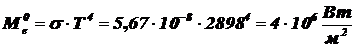 .
.
2) Для ЧТ из следствия из закона Ламберта (2.10): 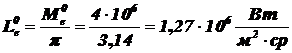 .
.
3) По формулам (1.3) и (1.5): 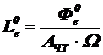 ;
; 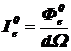 определяем:
определяем: 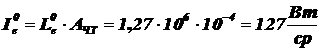 .
.
4) По формуле (1.4) находим: 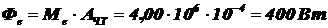 .
.
5) Определим световой поток, светимость, и яркость по формуле (1.11), если для ТЧТ = 2898 К из табл. 3 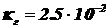 :
:
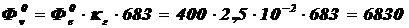 лм,
лм,
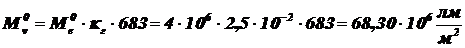 ,
,
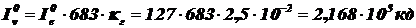 ,
,
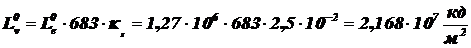
Ответ: 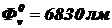 ,
, 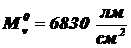 ,
, 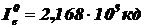 ,
, 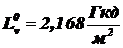 .
.
Задача 2.2.2
Определить энергетическую светимость объекта 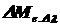 в спектральном интервале
в спектральном интервале 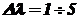 мкм при его температуре 1450 К,
мкм при его температуре 1450 К, 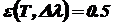 , а также какую долю составляет энергетическая светимость в указанном спектральном диапазоне по отношению к энергетической светимости данного объекта во всем диапазоне спектра излучения объекта.
, а также какую долю составляет энергетическая светимость в указанном спектральном диапазоне по отношению к энергетической светимости данного объекта во всем диапазоне спектра излучения объекта.
Дано: T = 1450 К; 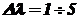 мкм;
мкм; 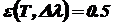 .
.
Определить: 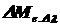 ,
, 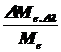 .
.
Решение:
1) Определим длину волны максимума излучения данного объекта по закону смещения Вина (2.4): 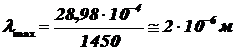 .
.
2) Затем по формуле (2.7) определим: 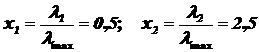 .
.
3) По табл. 5 найдем значения: 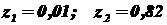 .
.
4) По формуле (2.9) определим, какую долю составляет энергетическая светимость 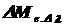 в указанном спектральном диапазонепо отношению к энергетической светимости данного объекта
в указанном спектральном диапазонепо отношению к энергетической светимости данного объекта 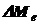 во всем диапазоне спектра:
во всем диапазоне спектра: 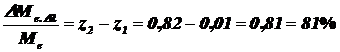 .
.
5) Определяем 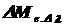 по закону Стефана - Больцмана (2.1) и формуле (2.3):
по закону Стефана - Больцмана (2.1) и формуле (2.3):
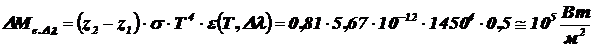 Ответ: Энергетическая светимость указанного объекта равна
Ответ: Энергетическая светимость указанного объекта равна 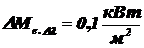 и составляет
и составляет 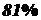 по отношению к энергетической светимости данного объекта во всем диапазоне спектра.
по отношению к энергетической светимости данного объекта во всем диапазоне спектра.
Задача 2.2.3
Определить энергетическую светимость ЧТ площадью 1 см2 в спектральном диапазоне от 0,4 до 1 мкм и поток излучения, падающий на ПОИ с диаметром ФЧЭ 0,8 см, находящийся на расстоянии 10 м от ЧТ, в названном интервале спектра, если температура ЧТ равна:
1) T1 = 3000 К;
2) T2 = 3500 К.
Плоскости ЧТ и ФЧЭ ПОИ параллельны.
Дано: 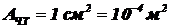 ;
; 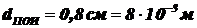 ;
; 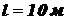 ;
; 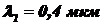 ;
; 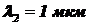 ;
; 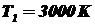 ;
; 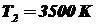 .
.
Определить:1) 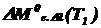 ,
, 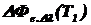 ;
;
2) 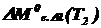 ;
; 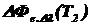 .
.
Решение:
1) при температуре 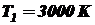 по закону Вина (2.5) определим длину волны, соответствующую максимальному значению СПЭС ЧТ:
по закону Вина (2.5) определим длину волны, соответствующую максимальному значению СПЭС ЧТ:
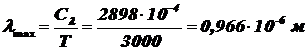 .
.
Далее по формуле (2.7) вычислим значения x1 и x2:
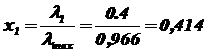 ,
, 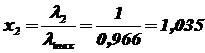
и по табл. 2 (см. приложение) находим значения z1 и z2:
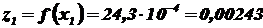 ;
; 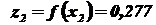 .
.
Для определения энергетической светимости в заданном спектральном интервале воспользуемся формулами (2.1) и (2.9):
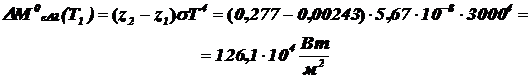
Поток излучения, падающий на ПОИ, согласно формулам (1.20) и (2.10) определяется как:
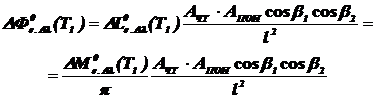
Поскольку плоскости ЧТ и ФЧЭ ПОИ параллельны, то
