Классификация кривых намагничивания

Различают следующие основные типы кривых намагничивания: первоначальные, петли гистерезиса, основные и средние.

Общие сведения.Характер изменения кривых намагничивания объясняется доменной теорией с привлечением соотношения

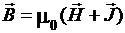. (3.19)

Для определённости и простоты изложения будем полагать, что магнитный материал имеет форму кольца и намагничивается током обмотки, намотанной равномерно по всей длине кольца. Это позволяет, очевидно, считать, что вектор 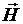в каждой точке кольца направлен перпендикулярно его радиусу и имеет одинаковую длину.

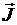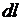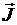Будем полагать также, что вектор есть результирующий вектор намагниченности материала, который определяется так. На кольце выбирается сектор малой толщины и объёма (рис. 3.4). Боковые поверхности сектора направлены по радиусу кольца. Исходя из определения намагниченности, будем считать, что для выбранного сектора вектор задаётся соотношением

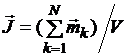, (3.20)

где 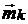– магнитный момент 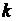-го атома (молекулы); 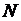– общее количество атомов (молекул).

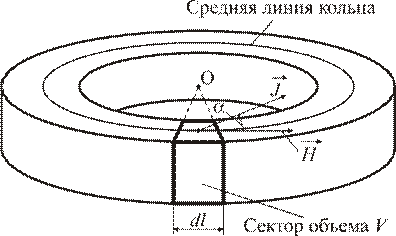
Рис. 3.4. Определение результирующего вектора

намагниченности 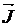вещества

Разобьем общую сумму магнитных моментов в (3.20) на отдельные суммы так, чтобы в каждую из них входили магнитные моменты только одного какого-либо домена. Тогда получим

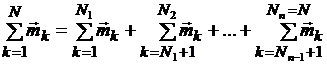, (3.21)

где 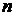– общее количество доменов; 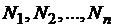– количество магнитных моментов соответственно в первом, втором и n-м доменах.

Учитывая, что намагниченность 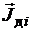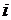-го домена определяется из равенства

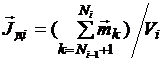, (3.22)

где 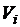– объём i-го домена, получаем из равенств (3.20)–(3.22) после преобразований

.

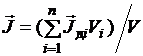Откуда после деления в последнем равенстве каждого слагаемого на объем V следует, что

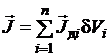, (3.23)

где 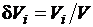– относительный объём 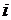-го домена.

Заметим, что вектор 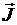в (3.23) составлен как сумма векторов 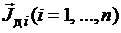со своими весовыми коэффициентами 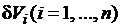и направлен в общем случае под некоторым углом 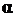(рис. 3.4) к средней линии, проходящей через выбранный сектор кольца. Заметим, что в силу (3.19) вектор 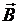также направлен в общем случае под некоторым углом к средней линии кольца. Но этот угол в общем случае отличается от угла α.

Как отмечалось выше, кривые намагничивания связывают проекции векторов 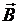и 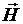на некоторое характерное направление рассматриваемого устройства. Будем считать, что в данном случае таким характерным направлением является средняя линия кольца. Проектируя векторы 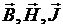на среднюю линию кольца, а также учитывая, что они связаны векторным соотношением (3.19), получаем, что

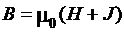, (3.24)

где 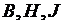– соответственно проекции векторов 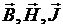на среднюю линию кольца.

Соотношение для величины 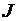в силу (3.23) примет, очевидно, следующий вид:

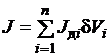, (3.25)

где 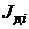– проекция вектора 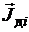на среднюю линию кольца ( 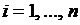). Заметим, что величины могут быть как положительными, так и отрицательными.

Соотношение (3.25) показывает, что с увеличением величин 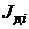( 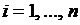), т.е. с увеличением степени сонаправленности намагниченности 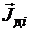i-го домена и средней линии кольца, а также с увеличением относительного объёма 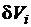i-го домена происходит увеличение результирующей намагниченности 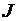материала кольца вдоль его средней линии.

Первоначальные кривые намагничивания.Первоначальной называют кривую намагничивания, полученную для изначально полностью размагниченного материала при условии его намагничивания магнитным полем, напряженность которого монотонно увеличивается.

Условие монотонного увеличения напряжённости означает, что в процессе такого намагничивания напряжённость с течением времени только увеличивается. Так как изменение напряжённости достигается технически изменением тока в обмотке кольца и напряжённость прямо пропорциональна току, то для монотонного увеличения напряжённости требуется монотонное увеличение тока.

Типичный вид первоначальной кривой намагничивания представлен на рис. 3.5. Эта кривая проходит через начало координат и разделяется на следующие участки: 0a – участок обратимого смещения границ доменов; ab – участок необратимого смещения границ доменов; bc – участок вращения; cd – участок парапроцесса.

Прохождение рассматриваемой кривой через начало координат объясняется так.

По условию в начале процесса намагничивания внешнее поле отсутствует, т.е. 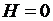. Это, во-первых. Во-вторых, магнитный материал размагничен, т.е. его собственное поле отсутствует. Последнее означает, что результирующая намагниченность материала 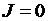. Тогда в силу (3.24) следует, что 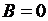. Это и означает, что первоначальная кривая должна проходить через начало координат (рис. 3.5).

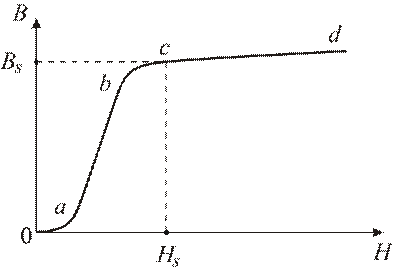
Рис. 3.5. Первоначальная кривая намагничивания

Возможность существования состояния магнитного материала с результирующей намагниченностью 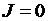объясняется доменной теорией тем, что в магнитном материале возможно равновероятное расположение намагниченностей доменов по различным направлениям. Это и даёт согласно (3.23) или (3.25) в сумме 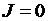. Физически такое состояние означает, что магнитные поля доменов компенсируют друг друга, обусловливая тем самым отсутствие результирующего собственного магнитного поля материала.

При увеличении напряжённости 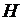на участке 0a происходит увеличение размеров тех доменов, намагниченности которых составляют острые углы с напряжённостью, и уменьшение размеров остальных доменов. Это вызывает согласно (3.25) увеличение результирующей намагниченности 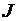материала в положительном направлении величины 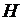. Название участка 0a обусловлено тем, что если снизить напряжённость 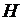вновь до нуля, т.е. обесточить намагничивающую обмотку, то границы доменов вновь восстановятся и материал окажется опять в целом размагниченным.

При увеличении напряжённости 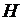на участке ab происходит интенсивный процесс скачкообразного изменения направлений векторов намагниченностей тех доменов, для которых эти векторы составляли первоначально достаточно большой угол с положительным направлением величины 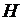. При таких скачках векторы намагниченностей указанных доменов устанавливаются в новом направлении легкого намагничивания, которое составляет с положительным направлением напряженности наименьший угол. Это означает, что в соотношении (3.25) интенсивно увеличивается количество слагаемых с положительными проекциями, что вызывает интенсивное увеличение намагниченности 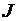и, как следствие, согласно (3.24) интенсивное увеличение магнитной индукции .

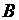На участке ab при увеличении напряжённости 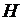так же, как и на участке 0a, происходит изменение границ доменов. Но если уменьшить напряжённость 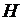после того, как она попала на участок ab, то границы доменов не восстановятся, т.е. произойдет необратимое изменение границ доменов.

При приближении к точке b все домены данного кристаллита оказываются сориентированными в том направлении легкого намагничивания этого кристаллита, которое составляет наименьший угол с положительным направлением напряженности H (см. рис. 3.6, а). Заметим, что для каждого кристаллита указанный наименьший угол имеет свое определенное значение. При достижении точки b на кривой намагничивания каждый кристаллит превращается в единый домен со своим направлением вектора намагниченности. Доменная структура магнитного материала, соответствующая точке b, имеет (при упрощённом представлении) вид, представленный на рис. 3.6, а. Здесь 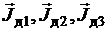– намагниченности соседних кристаллитов.

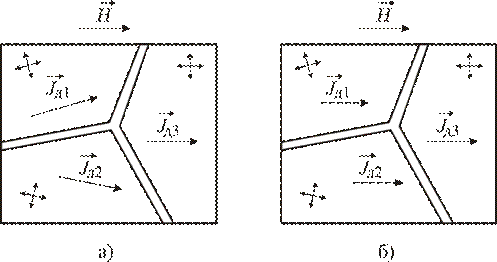
Рис. 3.6. Доменная структура магнитного материала при намагничивании по первоначальной кривой для точки b (а)

и точки c (б):

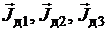– намагниченности соседних кристаллитов;

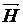– напряженность намагничивающего поля

При увеличении напряжённости 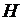на участке bс происходит вращение векторов намагниченностей 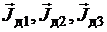в положительном направлении величины 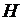, что увеличивает проекции этих векторов в указанном направлении и, как следствие, приводит к дальнейшему увеличению магнитной индукции .

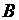При достижении точки с кривой намагничивания векторы намагниченностей кристаллитов выстраиваются в положительном направлении вектора напряжённости 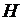параллельно друг другу (рис. 3.6, б). Такое состояние магнитного материала называется техническим насыщением, а соответствующие этому состоянию магнитная индукция, напряжённость и намагниченность – соответственно индукцией насыщения 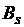, напряжённостью насыщения 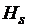и намагниченностью насыщения .

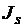Рассмотрим намагничивание на участке сd (участке парапроцесса). На этом участке векторы 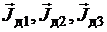при любом значении остаются направленными вдоль вектора 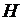и при этом не изменяют своей длины. Последнее объясняется тем, что векторы намагниченностей представляют собой суммы магнитных моментов атомов, а магнитные моменты атомов зависят только от температуры и химического состава материала. Таким образом, на участке сd проекции векторов намагниченностей кристаллитов 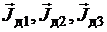достигают своих максимумов, т.е. длин этих векторов, и рост указанных проекций прекращается. Соответственно прекращается рост магнитной индукции за счёт намагниченности 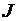материала, т.е. ресурсы увеличения магнитного поля в магнитопроводе за счёт магнитного материала оказываются исчерпанными. Дальнейший рост магнитной индукции 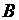происходит только за счёт напряжённости 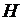, создаваемой током обмотки. Но этот рост незначителен до такой степени, что фактически можно считать, что на участке cd магнитная индукция не изменяется и имеет значение 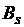. Поэтому на участке cd полагают, что 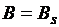, и говорят, что магнитный материал находится в состоянии насыщения или насыщенном состоянии. Говорят также, что при 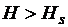магнитный материал попадает в состояние насыщения.

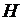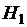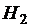Петли гистерезиса.П е т л я г и с т е р е з и с а – это кривая намагничивания, полученная при периодическом изменении напряжённости в пределах от до , где 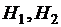– константы.

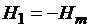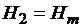При условии, что , а , где 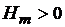– константа, петлю гистерезиса называют с и м м е т р и ч н о й.

При условии, что 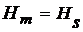, симметричную петлю гистерезиса называют предельной. В остальных случаях петли гистерезиса называют частными.

Петли гистерезиса, получаемые на постоянном токе, называют статическими. В остальных случаях петли гистерезиса называют динамическими.

Типичный вид симметричной петли гистерезиса приведен на рис. 3.7.

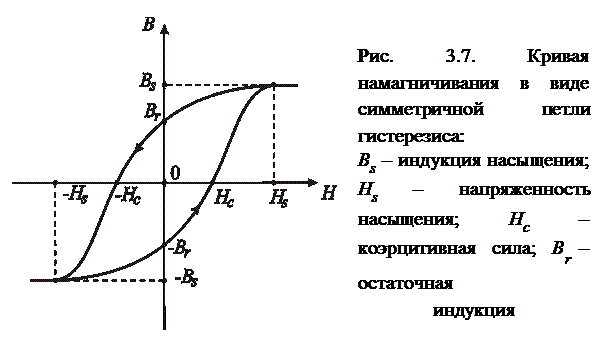
При увеличении напряженности Н магнитная индукция B изменяется по нижней части петли, а при уменьшении – по верхней, что отражено стрелками на петле. При таком взаимном изменении величин B и H нетрудно заметить, что изменение величины B отстает от изменения величины H. Например, при увеличении H от нулевого значения в положительном направлении величина B принимает вначале отрицательные значения и только затем положительные. Говорят, что изменение магнитной индукции запаздывает по отношению к изменению напряженности. Это обстоятельство и отражено в названии данной кривой намагничивания –­­­ петля гистерезиса ( от греч. – запаздывание ).

Дадим краткие пояснения по форме петли гистерезиса. Допустим, что по первоначальной кривой намагничивания произошло попадание магнитного материала в точку насыщения с координатами ( 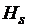, 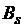). При нахождении в этой точке доменная структура, как это было показано ранее, имеет вид, представленный на рис. 3.6, б. Пусть далее обмотку, создающую магнитное поле в материале, обесточили. Следовательно, при этом магнитное поле обмотки исчезло, и напряженность H приняла нулевое значение (H = 0). Исчезновение поля приводит к тому, что намагниченности кристаллитов, представляющие собой, как отмечалось, единые домены, разворачиваются к ближайшим направлениям легкого намагничивания. Доменная структура материала в результате такого разворота приобретает вид, представленный на рис. 3.6, а. Таким образом, после обесточивания обмотки напряженность H = 0, результирующая намагниченность J материала уменьшается и, следовательно, согласно (3.24) уменьшается магнитная индукция В до некоторого значения 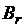, которое называется остаточной индукцией.

Из рис. 3.6 (а, б) нетрудно заметить, что степень уменьшения результирующей намагниченности J зависит от степени отклонения векторов 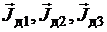от положительного направления напряженности или, иначе говоря, от степени дезориентации этих векторов при переходе по петле гистерезиса из точки 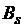в точку 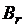. При этом нетрудно видеть, что чем больше степень дезориентации этих векторов, тем меньше оказываются их проекции на направление вектора H и тем меньше согласно (3.25) оказывается результирующая намагниченность J. Ясно, что чем меньше оказывается в этом случае намагниченность J, тем меньшего значения достигает остаточная индукция 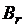и тем ближе проходит петля гистерезиса к началу координат.

Из рис. 3.6, а видно также, что степень дезориентации намагниченностей кристаллитов определяется степенью дезориентации их направлений легкого намагничивания, что в свою очередь определяется степенью дезориентации кристаллических решеток соседних кристаллитов. Таким образом, приходим к выводу: чем сильнее дезориентированы кристаллические решетки соседних кристаллитов, тем ниже остаточная индукция магнитного материала.

Дадим определения [11, с. 19]. Если оси легкого намагничивания кристаллитов в магнитном материале имеют практически одинаковую ориентацию, то такой материал называется текстурованным. Если оси легкого намагничивания кристаллитов ориентированы в материале беспорядочно, то такой материал называется магнитоизотропным.

В магнитоизотропных материалах, как это следует из вышеизложенного, остаточная индукция 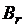имеет малые значения, а в текстурованных – весьма высокие. Для текстурованных материалов остаточная индукция 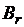= (0,9…0,95) 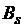, т.е. несущественно отличаются от индукции насыщения .

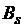Петли гистерезиса с весьма высокими значениями остаточной индукции называют прямоугольными.

Существует ряд способов создания текстурованных материалов [11, с. 19, 20]. Этот вопрос следует изучить САМОСТОЯТЕЛЬНО.

Продолжим рассмотрение характера изменения петли гистерезиса, положив, что состояние материала соответствует точке 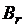, а напряженность H изменяет свой знак, т.е. направление. В точке 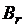каждый кристаллит представляет собой единый домен (рис. 3.6, а). При изменении направления вектора 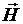поле обмотки действует против намагниченностей этих крупных доменов и разрушает их на более мелкие домены. При этом намагниченности некоторых из них поворачивается в новом направлении, что ведет к дальнейшему снижению результирующей намагниченности J. При некоторой напряженности 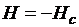(см. рис. 3.7) намагниченность J достигает такого значения 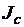, при котором оказывается, что 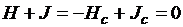и, следовательно, согласно (3.24) B = 0. Материал в точке 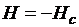оказывается в целом размагниченным.

Величина H_c называется коэрцитивной силой (от лат. сoercitio – удерживать).

При дальнейшем увеличении напряженности H в отрицательном направлении процесс намагничивания идет аналогично процессу намагничивания по первоначальной кривой. Процессы на нижней ветви петли гистерезиса аналогичны процессам, рассмотренным на верхней ветви.

Отметим далее несколько свойств петель гистерезиса.

1. Симметричная петля гистерезиса как геометрический объект практически однозначно определяется следующими величинами: индукцией насыщения Bs, напряженностью насыщения Hs, коэрцитивной силой Hcи остаточной индукцией Br. При этом индукция насыщения характеризует высоту петли гистерезиса, а коэрцитивная сила – ширину.

2. Динамические петли гистерезиса всегда шире статических, что объясняется влиянием магнитных полей вихревых токов и явлением магнитной вязкости. Причем динамическая петля одного и того же материала тем шире, чем выше скорость изменения магнитной индукции (напряженности) магнитного поля. Обоснование явления расширения петли гистерезиса в переменных магнитных полях следует изучить САМОСТОЯТЕЛЬНО [11, с. 26].

3. Площадь петли гистерезиса, как это можно показать, равна полным потерям энергии, которые выделяются в виде тепла в единице объема магнитного материала за один цикл перемагничивания. При определении площади петли линейные размеры по оси В следует задавать в единицах магнитной индукции, а по оси Н – в единицах напряженности.

Полные тепловые потери энергии в магнитном материале называют также магнитными потерями или потерями в стали. Полные тепловые потери энергии состоят из потерь на гистерезис, вихревые токи и магнитную вязкость. Потери на гистерезис определяют по статической петле. Вычитание потерь на гистерезис из полных потерь (при рассмотрении динамической петли) дает остальные потери.

Для многих магнитных материалов вихревые токи оказывают настолько существенное влияние на их характеристики, что возникает необходимость более детального рассмотрения явления вихревых токов.

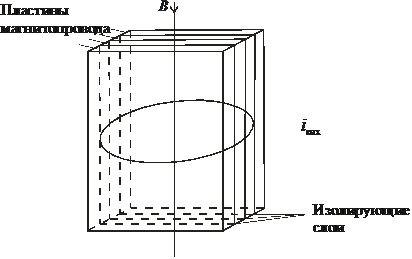
Вихревые токи. Допустим, что имеется магнитный материал в виде прямоугольного параллепипеда (см. рис. 3.8, а).

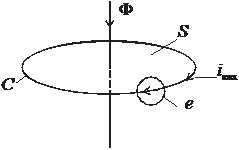
Допустим, что в этом материале действует переменное магнитное поле, показанное условно линией магнитной индукции В, направленной вдоль продольной оси параллепипеда. Выделим в материале бесконечно тонкую замкнутую электрическую цепь С, лежащую в плоскости, которая перпендикулярна линии магнитной индукции. В этой электрической цепи магнитный поток Ф (см. рис. 3.8, б), пронизывающий контур С площадью S, наводит по закону электромагнитной индукции ЭДС индукции е. Под действием ЭДС индукции е в цепи С возникает электрический ток i_вих, который и называют вихревым током.

а) б)

Рис. 3.8. Схема, поясняющая возникновение вихревых токов i_вих, (а)

и конструкция магнитопровода, снижающая вихревые токи (б)

Вихревой ток i_вих вызывает два эффекта: 1) создает в цепи С тепловые потери; 2) снижает результирующую магнитную индукцию в магнитном материале. Возникновение последнего эффекта необходимо показать САМОСТОЯТЕЛЬНО. Оба эффекта ухудшают характеристики электромашинных устройств и поэтому рассматриваются как отрицательные последствия явления вихревых токов. Рассмотрим меры борьбы с отрицательными последствиями вихревых токов.

Определим мощность рвихпотерь на вихревые токи. По закону Джоуля-Ленца

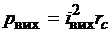, (3.26)

где 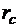– активное сопротивление контура С. Положив, что контур С имеет чисто активный характер электрического сопротивления, получим, что

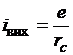. (3.27)

По закону электромагнитной индукции имеем

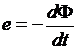. (3.28)

Положив далее, что магнитное поле является однородным, получим, что

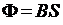. (3.29)

Преобразовав соотношения (3.26)–(3.29), получим

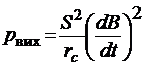, (3.30)

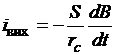. (3.31)

Из (3.30) и (3.31) видно, что при увеличении сопротивления 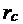магнитного материала мощность потерь на вихревые токи и сила вихревых токов уменьшаются. В свою очередь уменьшение вихревых токов приводит, как это нетрудно показать, к меньшему ослаблению магнитного поля вихревыми токами и, как следствие, к улучшению магнитных характеристик материала.

Из (3.30) и (3.31) видно также, что мощность потерь на вихревые токи и сила вихревых токов зависят еще и от скорости изменения магнитной индукции. Однако указанная скорость является при построении устройств, как правило, величиной заданной. Поэтому основной мерой борьбы с отрицательными последствиями явления вихревых токов – тепловыми потерями и ослаблением магнитного поля в магнитном материале – является увеличение активного сопротивления последнего.

Некоторые магнитные материалы (ферриты и магнитодиэлектрики, характеристика которых дается ниже) являются диэлектриками. Поэтому в них вихревые токи при частотах до нескольких десятков килогерц и сотен мегагерц относительно малы. Для таких материалов проблема увеличения их активного сопротивления практически не возникает. Однако есть и такие магнитные материалы (электротехнические стали и пермаллои, характеризуемые ниже), которые при весьма хороших магнитных характеристиках имеют низкое электрическое сопротивление. Для таких материалов возникает проблема искусственного увеличения их электрического сопротивления. Такое увеличение достигается путем разделения магнитного материала на тонкие пластины, электрически изолированные друг от друга, так, как это показано на рис. 3.8, б. Заметим, что плоскости пластин располагаются перпендикулярно плоскости цепи С, в которой протекает вихревой ток i_вих или, иначе говоря, параллельно линиям индукции магнитного поля, которое индуцирует этот вихревой ток (см. рис. 3.8, б).

Так как плоскости пластин магнитопровода параллельны линиям магнитной индукции, то на пути магнитного потока Ф нет воздушных и иных немагнитных слоев и, следовательно, магнитное сопротивление магнитопровода вдоль линий магнитной индукции не изменяется, оставаясь таким же низким, как и в случае сплошного магнитопровода. Следовательно, магнитный поток Ф и магнитная индукция остаются такими же высокими, как и в случае сплошного магнитопровода. Итак, составление магнитопровода из пластин, плоскости которых параллельны линиям магнитной индукции, не изменяет магнитных характеристик магнитопровода вдоль этих линий и существенно увеличивает электрическое сопротивление вихревым токам, что приводит к снижению потерь на вихревые токи в таком магнитопроводе.

Выше отмечалось, что ферриты и магнитодиэлектрики являются диэлектриками. Поэтому нет необходимости искусственно увеличивать их электрическое сопротивление разделением на пластины. Таким образом, ферритовые и магнитодиэлектрические магнитопроводы (сердечники) изготавливаются сплошными, без дополнительного разделения на изолированные слои.

Пластинчатая структура стальных и пермаллоевых магнитопроводов повышает их электрическое сопротивление. Но может обеспечить приемлемые потери на вихревые токи только на низких частотах (до 3–10 кГц). Поэтому электротехнические стали и пермаллои применяют только на частотах до 3–10 кГц. На высоких частотах (свыше 30 кГц) потери в стальных и пермаллоевых сердечниках достигают, несмотря на их пластинчатую структуру, неприемлемых значений. Поэтому на высоких частотах приходится использовать только ферритовые и магнитодиэлектрические сердечники. В диапазоне частот изменения магнитного поля от 3 до 30 кГц требуется, как правило, проведение более глубокого сравнительного анализа магнитных свойств магнитопроводов с целью выявления наиболее оптимального материала для их изготовления [14, с. 31].

Основные и средние кривые намагничивания.Основной называют кривую намагничивания, которая представляет собой геометрическое место вершин симметричных петель гистерезиса, вложенных друг в друга.

Средней называют кривую намагничивания, проведенную через середины горизонтальных отрезков, соединяющих нижнюю и верхнюю ветви петли гистерезиса.

Характерный вид основных и средних кривых намагничивания приведен в [11, с. 22, 24]. Основные и средние кривые намагничивания используются для упрощенного расчета электромашинных устройств.

Зависимость относительной магнитной проницаемости магнитного материала от напряженности. При упрощенных расчетах и качественном анализе работы электромашинных устройств часто используют зависимость 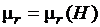. Эта зависимость определяется по экспериментальным кривым намагничивания расчетным путем с помощью формулы

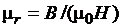. (3.32)

В качестве экспериментальных кривых намагничивания используют первоначальные, основные и средние кривые намагничивания. Типичный вид графиков зависимости 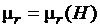приведен на рис. 3.9 (а, б). Здесь , – соответственно начальная и максимальная относительные магнитные проницаемости.

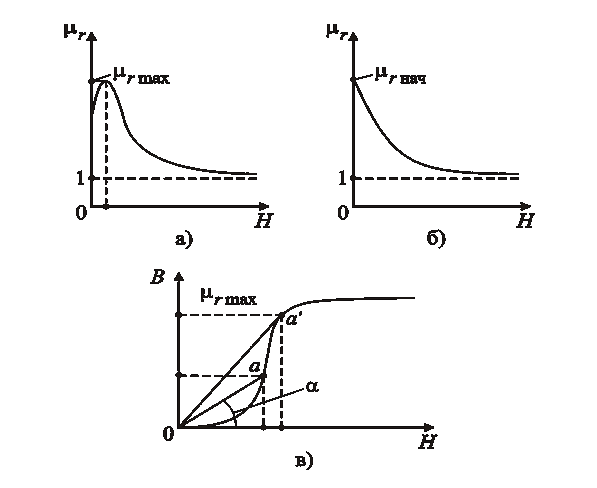
Рис. 3.9. Расчетное определение зависимостей

μr= μ r(H) (а , б) по экспериментальным

кривым намагничивания (в)

Характер изменения графика, представленного на рис. 3.9, а, можно пояснить, используя типичную кривую намагничивания, приведенную на рис. 3.9, в. Действительно, из этого рисунка видно, что 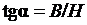. Тогда в силу (3.32) имеет место

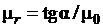.(3.33)

Из графика B(H) (см. рис. 3.9, в) видно также, что при увеличении H величина tgα увеличивается до тех пор, пока гипотенуза 0а не займет положение касательной 0а'. При дальнейшем увеличении H величина tgα уменьшается. Таким образом, величина tgα как функция переменной H имеет экстремальный характер изменения, достигая при некотором значении величины H максимального значения. Экстремальный характер изменения будет иметь в силу (3.33) также и величина .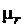

Покажем теперь, что при больших значениях напряженности магнитного поля в магнитном материале его относительная магнитная проницаемость 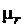приближается к значениям, близким к единице, т.е. покажем, что

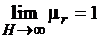. (3.34)

Для доказательства этого факта преобразуем вначале равенство (3.32) с учетом (3.24) к виду

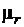=(J+H)/H = J/H +1.(3.35)

Перейдем далее в соотношении (3.35) к пределу при условии 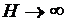, т.е. запишем

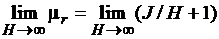. (3.36)

Так как при выполнении условия H> 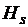намагниченность магнитного материала J достигает своего наибольшего значения 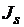, т.е. не превышает значения 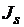при 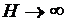, то, очевидно, что

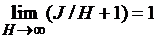. (3.37)

Подставляя (3.37) в (3.36), получаем (3.34), что и требовалось показать.

В силу изложенного график зависимости 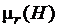будет иметь вид, изображенный на рис. 3.9, а.

В некоторых случаях, если кривая B(H) не имеет точек перегиба, зависимость 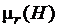, как это нетрудно показать геометрически, является монотонно убывающей функцией, график которой при 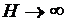асимптотически приближается к единице (см. рис. 3.9, б). Последнее обстоятельство доказывается так же, как и для зависимости 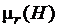с экстремальным характером изменения.

МАГНИТНЫЕ МАТЕРИАЛЫ

Магнитные материалы разделяют на две большие группы: магнитотвердые и магнитомягкие материалы. Критерием такого разделения является величина коэрцитивной силы магнитного материала.

Если магнитный материал имеет коэрцитивную силу 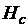> 4000 А/м, то его называют м а г н и т о т в е р д ы м, в противном случае магнитный материал называют м а г н и т о м я г к и м [10, с. 36].

Магнитотвердые материалы используются для изготовления постоянных магнитов, так как в силу большой коэрцитивной силы их невозможно размагнитить обыкновенными магнитными полями.

Магнитомягкие материалы используются для усиления магнитных потоков, создаваемых обмотками с током, и максимальной передачи магнитных потоков из одних обмоток в другие. Как правило, в устройствах с таким назначением магнитных материалов происходит изменение магнитных потоков (например, в трансформаторах), а значит, возникают магнитные потери в магнитных материалах. Эти потери, как отмечалось, определяются площадью петли гистерезиса, а площадь – величиной 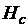. Для обеспечения малых магнитных потерь в таких устройствах необходимо, очевидно, применять материалы с малой коэрцитивной силой или, иначе говоря, магнитомягкие материалы.

Магнитомягкие материалы делят на [11, с. 29; 12, с. 120]:

1) электротехнические стали;

2) сплавы железа с другими металлами;

3) ферриты;

4) магнитодиэлектрики.

В ферритах имеет место явление ферримагнетизма, а в остальных указанных магнитных материалах – ферромагнетизма.

Электротехнические стали. Электротехнические стали – это сплавы железа с 0,4–4,8% кремния [12, с. 127; 15, c. 38]. Кремний предназначен для увеличения удельного электрического сопротивления и снижения тем самым потерь на вихревые токи [10, с. 39]. Одновременно кремний повышает магнитную проницаемость, а также хрупкость стали. Уже при 4–5% кремния электротехническая сталь выдерживает не более 1–2 перегибов на 90°. Учитывая при этом, что максимум магнитной проницаемости достигается при 6,5–6,8% кремния, электротехнические стали с содержанием кремния свыше 5% в технике не применяют [12, с. 127].

Электротехнические стали, кроме кремния, содержат примеси: углерод, серу, марганец, фосфор и др. Эти примеси ухудшают либо магнитные, либо механические свойства сталей. Для улучшения свойств сталей их очищают от примесей, а также подвергают термообработке. Однако существенно улучшить свойства сталей указанным образом не удается. Свойства стали значительно улучшаются при изготовлении ее методом холодной прокатки, т.е. прокатки без нагревания. В результате такой прокатки сталь становится текстурованным магнитным материалом, что и объясняет улучшение ее магнитных свойств. Сталь, полученная методом холодной прокатки, называется холоднокатаной. Деформация стали в холодном состоянии приводит к появлению в ней больших внутренних механических напряжений. Эти напряжения снимают отжигом. Отжиг состоит из нагрева стали до определенной температуры с заданной скоростью, выдержку при этой температуре и охлаждении с заданной скоростью.

Электротехнические стали являются наиболее дешевыми магнитными материалами, имеют большую индукцию насыщения ( 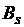= 1,8–2,3 Тл), относительно большую коэрцитивную силу и относительно большие магнитные потери.

Относительная магнитная проницаемость сталей составляет от единиц тысяч до десятков тысяч единиц.

Частотный диапазон применения сталей составляет от нуля до 10 кГц [14, с. 23]. Стали, предназначенные для работы на частот