Описание экспериментальной установки и метода исследования магнитного гистерезиса.

На рис. 4 изображена принципиальная электрическая схема, с помощью которой можно наблюдать петлю гистерезиса на экране осциллографа.

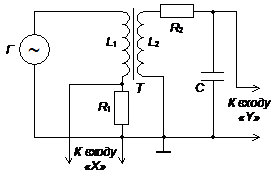
Рис. 4. Схема установки для наблюдения петли гистерезиса.

Рассмотрим принцип работы схемы. Ток, создаваемый генератором Г в первичном контуре, возбуждает в намагничивающей обмотке L₁ переменное магнитное поле напряжённостью:

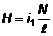, (6)

где i₁ – мгновенное значение силы тока, N - число витков в обмотке L₁; l – эффективная длина тороидального ферромагнитного магнитопровода трансформатора T. Напряжение, подаваемое с резистора R₁ на вход «X» (усилитель горизонтального отклонения) осциллографа, равно:

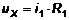. (7)

Из (6) и (7) получаем:

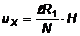(8)

Таким образом, горизонтально отклоняющее напряжение пропорционально напряжённости магнитного поля Н.

В свою очередь, в индикаторной катушке L₂ под действием переменного магнитного поля возникает эдс индукции:

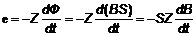, (9)

где Z - число витков в индикаторной катушке L₂, Ф - магнитный поток, S - площадь сечения магнитопровода трансформатора.

Для того чтобы подать на вход «Y» (усилитель вертикального отклонения) осциллографа напряжение, пропорциональное индукции магнитного поля B, между индикаторной катушкой и входом «Y» осциллографа включают интегрирующую RC-цепочку, удовлетворяющую условию R₂C >> Т, где Т - период переменного тока. При этом напряжение на конденсаторе будет пропорционально индукции магнитного поля B. Покажем это.

При R₂ >> 1/wC можно считать, что мгновенное значение силы тока в цепи индикаторной катушки равно:

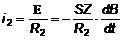. (10)

Напряжение на конденсаторе U_C равно:

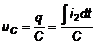. (11)

Поскольку u_Y = u_C, то из (10) и (11) следует, что

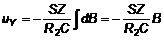. (12)

Таким образом, поскольку на горизонтально отклоняющие пластины осциллографа подается напряжение, пропорциональное Н, а на вертикально отклоняющие – пропорциональное В, то на экране будет отображаться зависимость В = f(Н).

За один период изменения синусоидального тока след электронного луча на экране опишет полную петлю гистерезиса, а за каждый последующий период в точности ее повторит. Поэтому на экране будет видно неподвижное изображение петли гистерезиса. Увеличивая напряжение, подводимое к намагничивающей обмотке, мы будем увеличивать амплитуду колебаний напряженности Н и получать на экране последовательно ряд различных по своей площади петель гистерезиса. Верхние точки семейства петель гистерезиса будут соответствовать кривой начального намагничивания.

Для построения графика кривой начального намагничивания (0-1 на рис.3) вычисляют значения B и Н верхних точек семейства петель гистерезиса в соответствии с формулами:

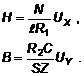(13)

В формулы (13) R₁ и R₂ подставляют в омах; С - в фарадах; S - в квадратных метрах; l - в метрах; U_x и U_y - в вольтах. Тогда Н будет выражено в амперах на метр (А/м), а величина В - в веберах на квадратный метр (Bб/м²). Используя изображение петли гистерезиса на экране осциллографа можно определить потери энергии на перемагничивание.

Намагничивая ферромагнетик, мы сообщаем ему энергию на создание магнитного поля внутри ферромагнетика и вне его. Плотность энергии магнитного поля определяется выражением:

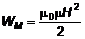, (14)

а так как B = m₀mH, то вместо (14) можно написать

.

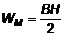Чтобы увеличить напряженность поля на величину dН (индукция поля соответственно возрастет на величину dВ), необходимо совершить работу:

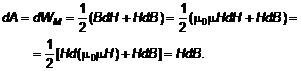(15)

(мы полагаем, что в небольшом интервале изменения поля dН магнитная проницаемость m остается постоянной).

Вычислим работу намагничивания единицы объёма ферромагнетика при изменении индукции от нуля до некоторого значения В₁. Эта работа равна

,

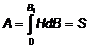Рис.5. Графическое представление работы намагничивания (а) и перемагничивания (б) ферромагнетика.

где S – площадь заштрихованной области на рис. 5а, т.е. работа намагничивания графически выражается площадью между кривой намагничивания и осью ординат.

Чтобы определить работу, необходимую для перемагничивания ферромагнетика, рассмотрим циклическое перемагничивание на некотором частном цикле ABCDA (рис.5б). Работа намагничивания А₁ выразится площадью ABCE . При уменьшении напряженности поля до первоначального значения ферромагнетик размагничивается и часть его энергии возвращается в цепь. Возвращаемую энергию можно рассматривать как отрицательную работу –А₂ источника тока, она равна площади ECDA. Таким образом, полная работа за цикл перемагничивания будет равна

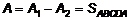. (16)

Увеличивая амплитуду изменений напряженности поля Н, мы можем перейти от частного цикла к максимальной петле гистерезиса. Тогда работа перемагничивания за один цикл будет равна площади максимальной петли. Таким образом, площадь петли гистерезиса есть мера потерь энергии в единице объема ферромагнетика за один цикл перемагничивания. При частоте перемагничивания n потери энергии в единице объема в единицу времени равны:

,

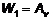а для всего образца

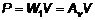, (17)

то есть P имеет смысл мощности потерь на перемагничивание.

Работа гистерезиса обычно не вычисляется по формуле А = ∫НdВ, так как зависимость В от Н весьма сложная, и вид функции В = f(H) как правило неизвестен. Поэтому либо непосредственно (графически) определяют площадь петли гистерезиса, либо с помощью калориметра измеряют тепло, выделяющееся в ферромагнетике. Можно измерять гистерезисные потери и с помощью моста переменного тока или с помощью ваттметра. Определяя потери в ферромагнитном образце с помощью калориметра или ваттметра, необходимо иметь в виду, что в этом случае мы находим полные потери энергии в образце, которые складываются из потерь на гистерезис и на вихревые токи.

Определим гистерезисные потери или потери на перемагничивание образца путем измерения площади петли гистерезиса. Подсчитаем площадь, т.е. количество клеток в петле гистерезиса в выбранном нами масштабе сетки. Следует отметить, что потери будут вычислены тем точнее, чем меньше масштаб сетки. Поэтому для точных вычислений применяется обычно миллиметровая бумага. В случае, если масштаб сетки выбран больше (например, масштаб обычной тетради «в клетку»), то необходимо с возможно большей точностью подсчитать не только целое число клеток внутри петли гистерезиса, но учесть и все доли клеток, попавшие внутрь петли.

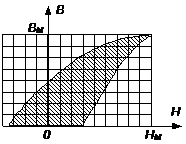Рис. 6. Определение площади петли гистерезиса.

Определим теперь потери энергии, приходящиеся на единицу площади (на одну клетку) петли гистерезиса за один цикл перемагничивания. Для этого воспользуемся соотношением:

,

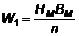где n - число клеток прямоугольника, стороны которого равны Н_М и В_М (рис.6). Величина W₁ определяет энергетический масштаб или энергетическую цену одной клетки за один цикл перемагничивания для единицы объема образца.

Тогда для всей петли гистерезиса (на рис. 6 показана только половина петли) потери будут равны:

,

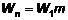где m - число клеток, охватываемых полной петлей гистерезиса:

,

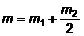где m₁ – число целых, а m₂ – число нецелых клеток, попадающих внутрь петли.

Для всего образца потери в единицу времени, т.е. мощность потерь, составят:

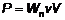, (18)

где V - объем образца, v- частота.