Исследование затухающих колебаний

Исследование затухающих колебаний

в колебательном контуре

Цель работы: изучить затухающие колебания в электрическом колебательном контуре. Определить период свободных затухающих колебаний, логарифмический декремент затухания и исследовать зависимость периода свободных колебаний от параметров контура.

Приборы и оборудование: осциллограф, лабораторный макет установки для возбуждения колебаний, конденсатор, две эталонных катушки индуктивности, переменное сопротивление, соединительные провода, дроссельная катушка 1200 витков.

КРАТКАЯ ТЕОРИЯ

Электрическими колебаниями называют периодические изменения тока и напряжения в электрической цепи. В общем случае в каждый момент времени при колебаниях ток на разных участках цепи оказывается не одинаковым, так как электромагнитные возмущения распространяются с конечной скоростью, хотя и с очень большой. Однако во многих случаях изменения тока происходят достаточно медленно и можно считать его одинаковым во всех участках цепи. Такой ток называют квазистационарным. Для расчётов квазистационарных токов можно пользоваться формулами для статических полей. В частности, можно применять закон Ома для мгновенных значений тока и напряжения.

Изучать электромагнитные колебания удобнее всего с помощью колебательного контура, состоящего из электрической ёмкости С и индуктивности L.

Свободные колебания происходят в изолированном контуре после подействовавшего на него внешнего возмущения. Понятие свободные колебания означает, что процесс колебаний в этом случае определяется (в основном) свойствами контура.

Для возбуждения колебаний в состав колебательного контура необходимо включить источник ЭДС Е и ключи К₁ и К₂, как показано на рис. 1.

Рис.1. Схема возбуждения колебаний в колебательном контуре.

В начальный момент ключ К₁ разомкнут, а ключ К₂ замкнут. После зарядки конденсатора до напряжения U₀ ключ К₂ размыкается, а ключ К₁ замыкается, и в колебательном контуре возникают электромагнитные колебания.

Начальные условия, при которых возникают свободные колебания, определяют начальную фазу процесса и амплитуду колебаний. Характер же процесса свободных колебаний, как следует из данного выше определения этого типа колебаний, зависит от свойств самой системы.

Напомним вкратце ход процесса электромагнитных колебаний в контуре, имеющий место при любых начальных условиях. Процесс колебаний в таком контуре заключается в периодической перезарядке конденсатора и протекании переменного тока в цепи, замыкающей пластины конденсатора. При этих колебаниях энергия электростатического поля заряженного конденсатора C периодически переходит в энергию магнитного поля, запасаемую в индуктивности L. В результате наличия в контуре неизбежного активного сопротивления R (сопротивления потерь энергии) первоначальный запас энергии системы расходуется (даже при отсутствии резистора) на выделение тепла в проводах, составляющих контур и индуктивность L. Поэтому разряд конденсатора через такой контур является процессом не вполне периодическим. Амплитуда напряжения на конденсаторе после каждой его перезарядки становится все меньше; амплитуда тока также убывает со временем.

Сила тока в контуре связана с зарядом и разностью потенциалов на конденсаторе соотношением:

,

где q = Cu - есть заряд конденсатора. Знак «минус» указывает на то, что положительным считается то направление тока, которое соответствует убыли разности потенциалов на пластинах конденсатора. Изменение силы этого тока в катушке индуктивности вызывает электродвижущую силу самоиндукции, равную

.

Согласно второму закону Кирхгофа u + e_i = iR. Подставляя значения e_i и i, получим:

или

(1)

Введём новые обозначения:

; , (2)

где a - коэффициент затухания; w₀ – циклическая частота собственных колебаний (колебаний без затухания), и перепишем формулу (1) в виде:

_. (3)

Уравнения (1) и (3) есть уравнения свободных колебаний в контуре, составленном из L, С и R. Если выполняется условие a < w₀, то решение уравнения (3) может быть записано в форме:

(4)

где есть циклическая частота свободных колебаний в контуре, U₀ и j - константы, зависящие от начальных условий колебательного процесса, а U_m – амплитуда.

Рис.2. Вид затухающих колебаний.

Из решения следует, что напряжение на конденсаторе U с течением времени изменяется по гармоническому закону с амплитудой колебаний, убывающей со временем по экспоненциальному закону:

, (5)

где U₀ - начальное напряжение на конденсаторе (при t = 0). Вид затухающих колебаний представлен на рис.2.

Период свободных колебаний выражается формулой

(6)

Если a << w₀, то членом R²/4L² можно пренебречь, и мы получим формулу Томсона:

, (7)

определяющую период свободных колебаний в контуре без затухания.

Величина a, определяющая степень затухания, называется коэффициентом затухания. На практике вместо нее часто употребляется другая мера затухания:

(8)

где U_n и U_n+1 - величины последовательных амплитуд, отстоящих друг от друга на один период. Величина g называется логарифмическим декрементом затухания. Ёе связь с a можно установить следующим образом. Так как U_n+1 = U_nЧe^-at, то U_n/U_n+1 = e^at. Отсюда следует:

Рис. 3. Апериодический режим колебаний.

. (9)

Из уравнения (9) видно, что чем меньше R и чем больше L, тем меньше затухание, тем ближе подходит описываемая выражением (4) кривая к гармонической функции, и тем ближе период Т к величине Т₀, определенной по формуле Томсона. Наоборот, при значительном возрастании R затухание, так же как и период, увеличивается. При a > w₀, когда вещественного решения уравнения (3) не существует, разряд будет изображаться кривой, приведенной на рис.3; такой процесс называется апериодическим. Режим, который разграничивает колебательный и апериодический процессы (a = w₀), называется критическим, а соответствующее сопротивление потерь в контуре определяется формулой:

(10)

ПРАКТИЧЕСКАЯ ЧАСТЬ

Описание установки. Схема установки для наблюдения осциллограммы свободных колебаний показана на рис. 4.

Рис. 4. Схема установки для наблюдения затухающих колебаний.

Рис. 5. Примерная осциллограмма напряжения на конденсаторе.

Конденсатор С, катушка индуктивности L и переменное сопротивление R образуют колебательный контур с потерями. Колебания в контуре (колебания напряжения на конденсаторе) наблюдаются с помощью осциллографа. Примерный вид осциллограммы показан на рис. 5. Диод VD предназначен для периодического возбуждения в контуре свободных колебаний. Рассмотрим упрощенно работу этой установки. В течение положительного полупериода питающего напряжения диод открыт (его сопротивление близко к нулю) и в контур поступает энергия; контур работает в режиме вынужденных колебаний, что соответствует участку I на рис. 5. При отрицательном полупериоде питающего напряжения диод заперт (его сопротивление очень велико) и в контуре наблюдается режим свободных затухающих колебаний (участок II на рис. 5).

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какой ток называют квазистационарным? Записать условия квазистационарности.

2. Какие колебания называются свободными колебаниями? Какими уравнениями описываются собственные колебания?

3. От чего зависит период свободных колебаний, какова эта зависимость?

4. Какими величинами характеризуют затухающие электромагнитные колебания?

5. Что такое логарифмический декремент затухания? Как он связан с коэффициентом затухания?

6. На основании каких рассуждений получена формула (7) для определения периода свободных колебаний?

7. Как определяется на опыте сопротивление потерь в контуре? Из чего складываются потери энергии в контуре (указать не менее трех возможных механизмов потерь)?

Лабораторная работа № 11

В ФЕРРоМАГНЕТИКе

Цель работы: исследовать явление магнитного гистерезиса, зарегистрировать кривую намагничивания ферромагнитного образца и определить потери энергии на перемагничивание.

Приборы и принадлежности: лабораторный стенд для наблюдения петли гистерезиса, двухканальный осциллограф, генератор, соединительные провода.

КРАТКАЯ ТЕОРИЯ

В общем случае вектор магнитной индукции в среде связан с напряженностью магнитного поля соотношением

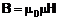, (1)

где m₀ = 4pЧ10^–7 Гн/м - магнитная постоянная; m- магнитная проницаемость среды (m = 1 для вакуума). Магнитная индукция в среде определяется индукцией в вакууме и намагниченностью среды:

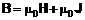, (2)

где J - вектор намагничивания, равный магнитному моменту единицы объема магнетика. Так как вектор J связан с вектором напряжённости магнитного поля соотношением:

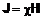, (3)

где c - магнитная восприимчивость среды, перепишем (2):

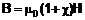. (4)

Из сравнения (1) и (4) следует, что

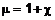. (5)

Магнитная восприимчивость и магнитная проницаемость характеризуют магнитные свойства вещества.

В зависимости от знака и величины восприимчивости c при нормальных условиях все вещества можно подразделить на три группы: диамагнетики, парамагнетики и ферромагнетики.

Парамагнетики характеризуются положительной восприимчивостью (c > 0), величина которой может принимать значения в интервале от 10^–5 до 10^–3. Во внешнем магнитном поле намагниченность парамагнетиков совпадает по направлению с внешним полем (J­­H).

Диамагнетики имеют отрицательное значение магнитной восприимчивости (c < 0) и имеют порядок величины 10^–6. Во внешнем магнитном поле намагниченность диамагнетиков противоположна направлению внешнего поля (J­¯H).

Рис. 1. Зависимость намагниченности от напряженности внешнего магнитного поля для пара- и диарамагнетиков.

Диа- и парамагнетики принадлежат к классу слабомагнитных веществ, их магнитная проницаемость близка к единице (абсолютное значение c очень мало).

В соответствии с формулой (3) существует линейная зависимость между J и H, как показано на рис. 1.

Вещества, в которых вектор намагничивания может значительно превышать по величине индукцию внешнего поля, называются ферромагнетиками.

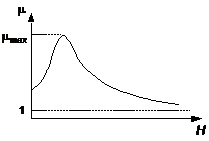Рис. 2. Зависимость магнитная проницаемости ферромагнетика от напряжённости магнитного поля

Ферромагнетики могут обладать спонтанной намагниченностью, то есть они намагничены при отсутствии поля. Магнитная восприимчивость c ферромагнетиков имеет высокое значение и может достигать величины 10³…10⁵. Магнитная проницаемость ферромагнетика является нелинейной функцией от напряжённости магнитного поля (рис. 2).

Рис.3. Петля гистерезиса.

Если ненамагниченный ферромагнетик поместить в пространство с постоянно увеличивающимся магнитным полем, то зависимость индукции магнитного поля внутри ферромагнетика B от напряжённости внешнего магнитного поля Н (рис.3) выразится участком 0-1 (начальная кривая намагничивания), вид которого определяется свойствами исследуемого магнетика.

Если продолжать увеличивать внешнее магнитное поле, то кривая намагничивания перейдёт в линейный участок, поскольку в результате насыщения величина намагниченности J станет постоянной, и B будет возрастать только за счёт увеличения H (см. выражение (2)).

При уменьшении напряжённости внешнего поля до нуля намагничивание будет изменяться в соответствии с кривой 1-2. Величина В_n, соответствующая отрезку 0-2 называется остаточной индукцией и является характеристикой ферромагнетика.

Остаточной индукции соответствует остаточная намагниченность J_n. Именно с наличием остаточной намагниченности связано существование постоянных магнитов. Остаточная намагниченность исчезает при температурах выше точки Кюри.

Остаточную индукцию можно устранить, если приложить к образцу обратное поле с напряжённостью –Н_c. Величина Н_c называется коэрцитивной силой и тоже является характеристикой ферромагнетика. При дальнейшем увеличении обратного намагничивающего поля вновь достигается насыщение. Если от точки насыщения 3 уменьшать магнитное поле до нуля, а затем, изменив направление, увеличивать поле, получим кривую намагничивания 3-4-1. Замкнутая кривая «1-2-3-4-1» называется петлёй гистерезиса.

Размеры петли гистерезиса увеличиваются с ростом амплитуды изменения напряжённости поля Н, но только до определённого предела (Н_m). Максимально возможная площадь петли соответствует случаю насыщения. Очевидно, что максимальное значение коэрцитивной силы Н_с и остаточной индукции В_n можно получить только по максимальной петле гистерезиса.

ПРАКТИЧЕСКАЯ ЧАСТЬ

Приложения

Порядок определение тока в первичной обмотке. Отжать кнопки X-Y (верхний ряд) и II (нижний ряд) на панели осциллографа; кнопка I нажата. По показаниям осциллографа измерить напряжение. Определить ток в первичной обмотке по измеренному напряжению и известному сопротивлению r = 30 Ом.

Порядок определение напряжения во вторичной обмотке. Отжать кнопки X-Y (верхний ряд) и I (нижний ряд) на панели осциллографа; кнопка II нажата. По показаниям осциллографа измерить напряжение. При этом амплитуду в клетках нужно умножить на число против риски аттенюатора Y - канала.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. Какие величины характеризуют магнитные свойства вещества? Как связаны между собой эти величины?

2. На какие классы делятся все вещества в зависимости от их магнитных свойств?

3. От чего зависит величина магнитной проницаемости ферромагнетика? Каковы эти зависимости?

4. Объясните ход намагничивания ферромагнетика во внешнем намагничивающем поле, учитывая доменную структуру ферромагнетика.

5. Каковы физические основы получения петли гистерезиса на экране осциллографа?

6. Как можно построить первоначальную кривую намагничивания по результатам опыта?

7. Как определяют потери энергии в ферромагнитном образце? Из чего складываются эти потери?

8. Как по форме петли гистерезиса можно судить о магнитных свойствах вещества? Что означают термины «мягкий» ферромагнетик, «жесткий» ферромагнетик? Где используют мягкие и жесткие ферромагнетики?

8. Дать объяснение пара- диамагнетизма, ферромагнетизма, рассматривая особенности взаимодействия молекул вещества с внешним полем.

Лабораторная работа № 12

Передача мощности в цепи постоянного тока

Цель работы: экспериментальное исследование зависимости полной мощности, полезной мощности и КПД источника постоянного тока от отношения сопротивлений нагрузки и источника.

Приборы и принадлежности: два источника ЭДС, амперметр, вольтметр, реостат.

КРАТКАЯ ТЕОРИЯ

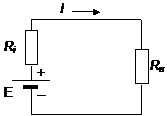Рис. 1. Эквивалентная схема источника ЭДС с подключённой нагрузкой.

Источник ЭДС Е с внутренним сопротивлением R_i, нагруженный на внешнее сопротивление нагрузки R_н, создает в цепи ток

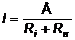. (1)

Эквивалентная схема такого источника имеет вид, показанный на рис. 1. Полная мощность P = ЕЧI, развиваемая источником, делится между нагрузкой R_н и источником R_i в том же отношении, что и напряжение:

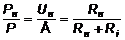, (2)

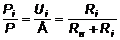, (3)

где Р_i – мощность, рассеиваемая внутри источника, Р_н - полезная мощность, выделяющаяся в нагрузке:

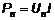, (4)

где U_н – напряжение на сопротивлении нагрузки.

Отношение h = P_н/P определяет коэффициент полезного действия (КПД) источника.

Полезная мощность источника и сопротивление нагрузки связаны соотношением:

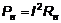.(5)

Воспользуемся соотношением (1) и получим:

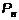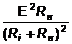= (6)

Исследование формулы (6) показывает, что с увеличением внешнего сопротивления R_н от нуля (режим короткого замыкания) до бесконечности (цепь разомкнута) напряжение U_н на нагрузке возрастает от нуля до значения, равного ЭДС, а ток в цепи уменьшается от величины I_к.з. = Е /R_i (при коротком замыкании цепи), до нуля. Полезная мощность Р_н равна нулю как при коротком замыкании, так и при разомкнутой цепи.

Максимальное значение полезной мощности Р_н.max достигается при равенстве сопротивлений нагрузки и внутреннего сопротивления источника ЭДС, т.е. при R_н = R_i. В случае такого равенства сопротивлений получаем в цепи согласованный режим источника и нагрузки, при котором, как легко показать, P_н.max = Е²/4R_i. Полная мощность Р с увеличением сопротивления нагрузки уменьшается и в режиме согласования составляет Р = Е²/(2R_i) - это половина мощности, развиваемой источником в режиме короткого замыкания (P_к.з. = Е²/R_i).

Внешнее напряжение источника U_н в режиме согласования равно половине ЭДС: КПД источника h в этом режиме составляет 0,5.

ПРАКТИЧЕСКАЯ ЧАСТЬ

КОНТРОЛЬНЫЕ ЗАДАНИЯ И ВОПРОСЫ

1. Записать основные характеристики постоянного электрического тока.

2. Записать закон Ома в дифференциальной форме.

3. Что такое электродвижущая сила?

4. Принцип действия химических источников ЭДС.

5. Чем отличается ЭДС от напряжения на клеммах источника энергии?

6. Как определить полезную и полную мощность источника ЭДС?

7. Доказать, что максимальная полезная мощность соответствует равенству R_н = R_i.

Лабораторная работа № 13

ИЗУЧЕНИЕ ЭФФЕКТА Холла

Цель работы: ознакомиться с явлением Холла и методикой измерения, измерить э.д.с. Холла, определить холловскую константу и концентрацию электронов в образце.

Приборы и принадлежности: датчик Холла, электромагнит, измерительные приборы, осциллограф, генератор, соединительные провода.

КРАТКАЯ ТЕОРИЯ

Электропроводность металлов зависит от концентрации электронов проводимости n и от их подвижности b. Обе эти величины, являющиеся важными характеристиками металла, могут быть определены из опыта.

Для измерения концентрации электронов чаще всего пользуются явлением Холла. Рассмотрим проводник в виде прямоугольной пластины, в которой течет ток с плотностью j(рис.1а).

Рис.1. Возникновение поперечной разности потенциалов в проводнике с током j под действием поперечного магнитного поля с индукцией B.

Эквипотенциальными поверхностями внутри такой пластинки будут плоскости, перпендикулярные к направлению тока, и поэтому разность потенциалов между двумя металлическими зондами 1 и 2, лежащими в одной из этих плоскостей, будет равна нулю.

Если поместить образец в магнитное поле B, перпендикулярное току и зондам (рис.1б), то между зондами возникнет разность потенциалов (э.д.с. Холлла), указывающая на то, что при наличии магнитного поля эквипотенциальные плоскости в пластинке становятся наклонными.

Явление Холла просто объясняется электронной теорией и является следствием существования силы Лоренца. Чтобы понять физическую сущность этого явления, ограничимся упрощенной его теорией и будем приближенно считать, что все электроны движутся с постоянной скоростью, равной средней скорости их упорядоченного движения v. Тогда на каждый электрон действует сила Лоренца, перпендикулярная направлению тока и магнитному полю:

, (1)

где е – заряд электрона.

Под действием этой силы электроны будут смещаться, так что одна из граней пластинки зарядится отрицательно, а другая - положительно, и внутри пластинки возникает поперечное электрическое поле E. При равновесии сила, действующая на электроны со стороны электрического поля, равна силе Лоренца:

(2)

Если толщина пластин d, холловская разность потенциалов их будет:

.

Среднюю скорость электронов v можно выразить через плотность тока j, так как j = nev, и получим:

, (3)

где R = - называют постоянной Холла. Постоянная Холла зависит от концентрации электронов n, и поэтому, измеряя постоянную Холла, можно определить концентрацию электронов внутри проводника или полупроводника.

Легко также видеть, что знак поперечной разности потенциалов зависит от знака заряда подвижных частиц, обуславливающих электропроводность. Действительно, пусть в проводящей пластине ток течет слева направо (рис.2а). Если подвижные частицы в проводнике несут положительный заряд, то скорость этих частиц имеет то же направление, что и ток, и при указанном направлении магнитного поля сила Лоренца будет направлена снизу вверх. В этом случае верхняя грань пластины будет заряжаться положительно, а нижняя - отрицательно.

Рис.2а.

Рис.2б.

Если же частицы заряжены отрицательно, то их скорость направлена противоположно току (рис.2б). Так как сила Лоренца зависит и от заряда частиц, и от их скорости, то ее направление не изменится, и поэтому заряженные частицы так же будут накапливаться у верхней грани. Однако, так как частицы заряжены отрицательно, верхняя грань будет заряжаться отрицательно, а нижняя - положительно, т.о. э.д.с. Холла будет иметь обратный знак. Измеряя э.д.с. Холла U_Х, индукцию магнитного поля B, в котором находится образец, силу тока I в образце и, зная ширину образца а, можно определить знак основных носителей заряда, постоянную Холла R и вычислить концентрацию носителей зарядов n.

Действительно, пользуясь соотношением (3) и учитывая, что плотность тока j = I/S, где S = ad - площадь поперечного сечения образца, можно найти постоянную Холла:

. (4)

Так как R = 1/(ne), получим:

. (5)

Зная же удельную электропроводность l = enb, можно найти произведение nb и, следовательно, определить подвижность b носителей заряда.

ПРАКТИЧЕСКАЯ ЧАСТЬ

КОНТРОЛЬНЫЕ ЗАДАНИЯ И ВОПРОСЫ

1. Как объяснить явление Холла на основе электронной теории проводимости?

2. Где проявляется эффект Холла сильнее: в проводниках или полупроводниках? Почему?

3. Как это следует понимать согласованное включение катушек электромагнита?

4. Что произойдет, если изменить полярность включения катушек электромагнита на обратную?

5. Для чего используются датчики Холла на практике?

6. Как по результатам эксперимента определить подвижность носителей заряда? Вывести расчетную формулу.

Рекомендуемая ЛИТЕРАТУРА.

1. Калашников С.Г. Электричество. – М.: Наука, 1970.

2. Фриш С.Э., Тимофеева А.В. Курс общей физики. Т.2.–М.: Физматгиз, 1962.

3. Руководство к лабораторным занятиям по физике. Под ред. Л.Л.Гольдина. – М.: Наука, 1973.

4. Практикум по общей физике. Под ред. проф. В.Ф.Ноздрева. – М.: Просвещение, 1971.

5. Савельев И.В. Курс физики, т.II, Электричество. – М.: Наука, 1973.

6. Матвеев А.Н. Электричество и магнетизм. – М.: Высшая школа, 1983.

7. Сивухин Д.В. Общий курс физики. Электричество. – М.: Наука, 1983.

физический практикум

«электричество и магнетизм» часть 3

Учебно-методические рекомендации

для студентов физического факультета

Михеев Владимир Александрович

Монтанари Сергей Георгиевич

Дубов Владимир Петрович

Печать офсетная

Подписано в печать _________________ Заказ №_____________

Объем __________ п.л. Тираж _________________ экз.

Издательство Тюменского государственного университета

625003, г. Тюмень, ул. Семакова, 10

Исследование затухающих колебаний

в колебательном контуре

Цель работы: изучить затухающие колебания в электрическом колебательном контуре. Определить период свободных затухающих колебаний, логарифмический декремент затухания и исследовать зависимость периода свободных колебаний от параметров контура.

Приборы и оборудование: осциллограф, лабораторный макет установки для возбуждения колебаний, конденсатор, две эталонных катушки индуктивности, переменное сопротивление, соединительные провода, дроссельная катушка 1200 витков.

КРАТКАЯ ТЕОРИЯ

Электрическими колебаниями называют периодические изменения тока и напряжения в электрической цепи. В общем случае в каждый момент времени при колебаниях ток на разных участках цепи оказывается не одинаковым, так как электромагнитные возмущения распространяются с конечной скоростью, хотя и с очень большой. Однако во многих случаях изменения тока происходят достаточно медленно и можно считать его одинаковым во всех участках цепи. Такой ток называют квазистационарным. Для расчётов квазистационарных токов можно пользоваться формулами для статических полей. В частности, можно применять закон Ома для мгновенных значений тока и напряжения.

Изучать электромагнитные колебания удобнее всего с помощью колебательного контура, состоящего из электрической ёмкости С и индуктивности L.

Свободные колебания происходят в изолированном контуре после подействовавшего на него внешнего возмущения. Понятие свободные колебания означает, что процесс колебаний в этом случае определяется (в основном) свойствами контура.

Для возбуждения колебаний в состав колебательного контура необходимо включить источник ЭДС Е и ключи К₁ и К₂, как показано на рис. 1.

Рис.1. Схема возбуждения колебаний в колебательном контуре.

В начальный момент ключ К₁ разомкнут, а ключ К₂ замкнут. После зарядки конденсатора до напряжения U₀ ключ К₂ размыкается, а ключ К₁ замыкается, и в колебательном контуре возникают электромагнитные колебания.

Начальные условия, при которых возникают свободные колебания, определяют начальную фазу процесса и амплитуду колебаний. Характер же процесса свободных колебаний, как следует из данного выше определения этого типа колебаний, зависит от свойств самой системы.

Напомним вкратце ход процесса электромагнитных колебаний в контуре, имеющий место при любых начальных условиях. Процесс колебаний в таком контуре заключается в периодической перезарядке конденсатора и протекании переменного тока в цепи, замыкающей пластины конденсатора. При этих колебаниях энергия электростатического поля заряженного конденсатора C периодически переходит в энергию магнитного поля, запасаемую в индуктивности L. В результате наличия в контуре неизбежного активного сопротивления R (сопротивления потерь энергии) первоначальный запас энергии системы расходуется (даже при отсутствии резистора) на выделение тепла в проводах, составляющих контур и индуктивность L. Поэтому разряд конденсатора через такой контур является процессом не вполне периодическим. Амплитуда напряжения на конденсаторе после каждой его перезарядки становится все меньше; амплитуда тока также убывает со временем.

Сила тока в контуре связана с зарядом и разностью потенциалов на конденсаторе соотношением:

,

где q = Cu - есть заряд конденсатора. Знак «минус» указывает на то, что положительным считается то направление тока, которое соответствует убыли разности потенциалов на пластинах конденсатора. Изменение силы этого тока в катушке индуктивности вызывает электродвижущую силу самоиндукции, равную

.

Согласно второму закону Кирхгофа u + e_i = iR. Подставляя значения e_i и i, получим:

или

(1)

Введём новые обозначения:

; , (2)

где a - коэффициент затухания; w₀ – циклическая частота собственных колебаний (колебаний без затухания), и перепишем формулу (1) в виде:

_. (3)

Уравнения (1) и (3) есть уравнения свободных колебаний в контуре, составленном из L, С и R. Если выполняется условие a < w₀, то решение уравнения (3) может быть записано в форме:

(4)

где есть циклическая частота свободных колебаний в контуре, U₀ и j - константы, зависящие от начальных условий колебательного процесса, а U_m – амплитуда.

Рис.2. Вид затухающих колебаний.

Из решения следует, что напряжение на конденсаторе U с течением времени изменяется по гармоническому закону с амплитудой колебаний, убывающей со временем по экспоненциальному закону:

, (5)

где U₀ - начальное напряжение на конденсаторе (при t = 0). Вид затухающих колебаний представлен на рис.2.

Период свободных колебаний выражается формулой

(6)

Если a << w₀, то членом R²/4L² можно пренебречь, и мы получим формулу Томсона:

, (7)

определяющую период свободных колебаний в контуре без затухания.

Величина a, определяющая степень затухания, называется коэффициентом затухания. На практике вместо нее часто употребляется другая мера затухания:

(8)

где U_n и U_n+1 - величины последовательных амплитуд, отстоящих друг от друга на один период. Величина g называется логарифмическим декрементом затухания. Ёе связь с a можно установить следующим образом. Так как U_n+1 = U_nЧe^-at, то U_n/U_n+1 = e^at. Отсюда следует:

Рис. 3. Апериодический режим колебаний.

. (9)

Из уравнения (9) видно, что чем меньше R и чем больше L, тем меньше затухание, тем ближе подходит описываемая выражением (4) кривая к гармонической функции, и тем ближе период Т к величине Т₀, определенной по формуле Томсона. Наоборот, при значительном возрастании R затухание, так же как и период, увеличивается. При a > w₀, когда вещественного решения уравнения (3) не существует, разряд будет изображаться кривой, приведенной на рис.3; такой процесс называется апериодическим. Режим, который разграничивает колебательный и апериодический процессы (a = w₀), называется критическим, а соответствующее сопротивление потерь в контуре определяется формулой:

(10)

ПРАКТИЧЕСКАЯ ЧАСТЬ

Описание установки. Схема установки для наблюдения осциллограммы свободных колебаний показана на рис. 4.

Рис. 4. Схема установки для наблюдения затухающих колебаний.

Рис. 5. Примерная осциллограмма напряжения на конденсаторе.

Конденсатор С, катушка индуктивности L и переменное сопротивление R образуют колебательный контур с потерями. Колебания в контуре (колебания напряжения на конденсаторе) наблюдаются с помощью осциллографа. Примерный вид осциллограммы показан на рис. 5. Диод VD предназначен для периодического возбуждения в контуре свободных колебаний. Рассмотрим упрощенно работу этой установки. В течение положительного полупериода питающего напряжения диод открыт (его сопротивление близко к нулю) и в контур поступает энергия; контур работает в режиме вынужденных колебаний, что соответствует участку I на рис. 5. При отрицательном полупериоде питающего напряжения диод заперт (его сопротивление очень велико) и в контуре наблюдается режим свободных затухающих колебаний (участок II на рис. 5).