Принцип работы инерциальных систем

По способу определения местоположения движущегося объекта инерциальные системы навигации относятся к системам счисления пути. Счисление пути в них производится двойным ин­тегрированием ускорений, испытываемых движущимся объектом за время движения.

Измерителями ускорений являются специальные устройства, называемые акселерометрами.

Принцип работы инерциальных систем известен довольно дав­но, однако приемлемые для практики системы появились только в пятидесятые годы на­шего столетия, посколь­ку точность работы инерциальных систем зависит от точности элементов ее состав­ляющих: акселеромет­ров, гироскопов, счет­но-решающих устрой­ств и т. д.

Инерциальные сис­темы навигации пол­ностью автономны и помехоустойчивы. Их работа не зависит ни от работы радиотехнических средств, ни от магнитного поля Земли, ни от атмосферных условий и других факторов, что естественно полностью удовлетворяет требованиям безопасности полетов.

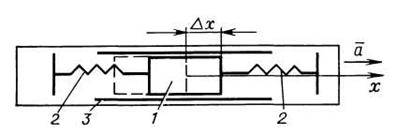
Рис. 10.1. Принципиальная схема акселерометра:

1– масса; 2 – пружины; 3 – направляющие

Основным чувствительным элементом инерциальной системы является акселерометр. Известно большое количество различных конструкций акселерометров для измерения линейных и угловых ускорений, но в каждом из них имеется некоторая масса и измере­ние ускорения сводится либо к измерению перемещения этой мас­сы под действием ускорения, либо к измерению сил, действующих на эту массу.

Простейший акселерометр для измерения линейных ускорений представляет собой массу 1 (рис. 10.1),связанную с корпусом прибора пружинами 2. Масса 1 может перемещаться относитель­но корпуса прибора по направляющим 3 вдоль оси измерения или оси чувствительности х. Корпус прибора жестко крепится на объ­екте (самолете).

Если самолет находится в покое или движется с постоянной скоростью в направлении оси чувствительности, то масса 1 не перемещается по направляющим, поскольку отсутствуют силы, растягивающие пружины. При движении самолета по направле­нию оси х с ускорением а масса 1 в силу своей инерционности бу­дет отставать от движения самолета, так как согласно второму закону Ньютона на нее будет действовать инерционная сила:

F = ma, (10.1)

где т — масса чувствительного элемента; а — ускорение.

Эта сила и вызывает перемещение массы в сторону, противо­положную действию ускорения. Движение массы будет продолжаться до тех пор, пока сила противодействия пружин F_пр не урав­новесит инерционную силу, следовательно, имеет место уравнение

F = F_пр (10.2)

Поскольку противодействующая сила пружины зависит от жестко­сти пружины и величины ее растяжения, то

F_пр = с∆х, (10.3)

где с — удельная жесткость пружины; ∆х — перемещение чувстви­тельной массы. Таким образом, исходя из выражений (10.2) и (10.3),

∆х = ma/c. (10.4)

Поскольку масса и жесткость пружины в приборе постоянны, то перемещение массы является мерой действующего ускорения.

Следует заметить, что акселерометр не измеряет ускорения си­лы тяжести, вызванного гравитационной силой, так как поле тяго­тения в одинаковой степени воздействует как на чувствительную массу, так и на самолет. Акселерометр, будучи установленный на тело, свободно падающее в безвоздушном пространстве, будет иметь нулевые показания.

Таким образом, инерциальная система навигации путем двой­ного интегрирования ускорения самолета осуществляет определе­ние пройденного пути. Для определения местоположения самолета в любой момент времени необхо­димо также знать и направление движения его, т. е. измерительная ось акселерометра должна быть определенным образом ориентиро­вана относительно вектора путе­вой скорости самолета в горизон­тальной плоскости.

В то же время акселерометр должен измерять только горизон­тальные ускорения самолета, для чего его измерительная ось долж­на быть определенным образом ориентирована и в горизонталь­ной плоскости, причем требования к такой ориентации весьма жесткие.

Для построения инерциальной системы навигации необходимо аксе­лерометры ориентировать относительно плоскости горизонта с большой точно­стью и стабилизировать их в этом положении во время полета в условиях непрерывных возмущений.

Как известно, для стабилизации каких-либо устройств в горизонтальной плоскости на движущемся объекте используются гироскопические вертикали с маятниковой коррекцией. Однако такие вертикали, например ЦГВ-4, не облада­ют необходимой точностью построения и выдерживания направления вертикали, так как подвержены влиянию ускорений объекта.

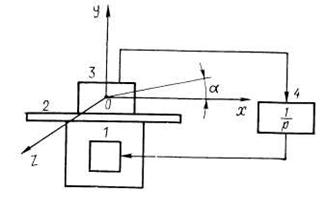
Рис. 10.2. Модель гиромаятника:

1 – гироскоп; 2 – платформа; 3 – акселерометр; 4 - интегратор

В 1923 г. немецкий ученый Макс Шулер теоретически показал, что физи­ческий маятник, длина которого равен радиусу Земли, а период колебаний при этом равен 84,4 мин, является невозмущаемым, т. е. не при каких ускорениях точки подвеса его плечо не отклоняется от направления вертикали места на Земле Естественно, что построить такой маятник не представляется возможные, но его можно моделировать. В 1932 г. советские ученые Е. Б. Левенталь и Л. М Кофман, предложили модель маятника с периодом колебаний 84,4 мин. Модель маятника представ­ляет собой гироскоп 1 с вертикальным кинетическим моментом (рис. 10.2). На платформе 2, стабилизируемой гироскопом 1, установлен акселерометр 3, изме­ряющий ускорения платформы. Сигнал, снимаемый с акселерометра, интегри­руется в интеграторе 4 и поступает на датчик момент гироскопа, располагае­мый на оси гироскопа параллельной оси измерения ускорений, заставляя гиро­скоп прецессировать.

Рассматриваемая механическая система, состоящая из акселерометра, инте­гратора и гироскопа, не будет реагировать на внешние ускорения

Выше была рассмотрена плоская модель невозмущаемого маятника (гиро­вертикали). Для построения пространственной вертикали необходимо устано­вить на платформу еще один акселерометр, ось чувствительности которого будет направлена по оси Oz; проинтегрировав ускорения, замеренные вторым акселерометром, заставить прецессировать еще один гироскоп вокруг оси Oz.

Таким образом возможно построение прецизионной гироскопической верти­кали, не возмущаемой ускорениями, которая сможет удовлетворить требовани­ям к стабилизации в плоскости горизонта акселерометров инерциальной систе­мы навигации.

ТИПЫ ИНЕРЦИАЛЬНЫХ СИСТЕМ

Инерциальная система навигации состоит, как правило, из следующих групп элементов:

1) устройства для определения вертикали места;

2) устройства для измерения и интегрирования ускорений;

3) счетно-решающей части и указывающих приборов.

Взаимная связь блока измерителей ускорений и гироскопиче­ских устройств, обеспечивающих ориентацию акселерометров в пространстве, определяет тип инерциальной системы. Известно три основных типа инерциальных систем.

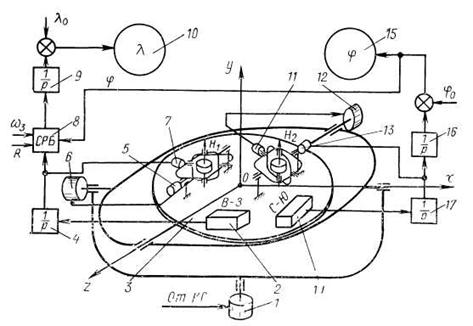
Рис. 10.3. Принципиальная схема инерциальной системы на­вигации:

1, 6, 12—двигатели; 2, 14—акселерометры; 3—платформа; 4, 9, 16, 17— интеграторы; 5, 11—датчики угла; 7, 13—датчики моментов; 8—счетно-решающий блок; 10, 15—индикаторы

1. Инерциальная система геометрического типа. В этих систе­мах блок гироскопов ориентируется и стабилизируется в инерциальном пространстве, а платформа с акселерометрами ориентиру­ется в горизонтальной плоскости и следит за положением местной
вертикали. Координаты места движущегося объекта получаются
измерением углов между платформой с акселерометрами и бло­ком гироскопов.

2. В инерциальной системе полуаналитического типа акселеро­метры и гироскопы находятся на одной платформе, причем прецес­сия гироскопов, а за ними и поворот платформы вызываются сиг­налами, снимаемыми с акселерометров. Координаты местоположе­ния объекта определяются в счетно-решающем устройстве, распо­ложенном вне платформы.

3. В инерциальных системах аналитического типа и акселеро­метры и гироскопы неподвижны в инерциальном пространстве. Координаты объекта получаются в счетно-решающем устройстве, в котором обрабатываются сигналы, снимаемые с акселерометров и устройств, определяющих поворот самого объекта относительна гироскопов и акселерометров.

Выбор типа инерциальной системы зависит от возможностей размещения инерциальной системы на движущемся объекте, си­стемы координат, в которой происходит счисление пути, наличия средств коррекции и средств начальной ориентации системы и т. д.

Рассмотрим одну из возможных принципиальных схем инер­циальной системы навигации второго типа (рис. 10.3).

Платформа 3 помещена в карданов подвес, внешняя ось кото­рого крепится к корпусу самолета. Двигатель 1 управляется от какой-либо курсовой системы, ориентируя ось Ох платформы по направлению Восток — Запад, а ось Oz — по направлению Се­вер — Юг. На платформе установлены акселерометры 2 и 14. Аксе­лерометр 2 всегда ориентирован по направлению Восток — Запад и измеряет горизонтальные ускорения самолета в этом направле­нии, акселерометр 14 — в направлении Север — Юг.

Ориентирование оси Оу по направлению местной вертикали осуществляется системой, куда входят: акселерометры 2 и 14, ин­теграторы 4 и 17, трехстепенные гироскопы с вертикальными ки­нетическими моментами Н₁ и Н₂, двигатели стабилизации 6 и 12. Параметры системы выбираются такими, чтобы они представляли собой невозмущаемую гировертикаль с периодом колебаний Т = 84,4 мин.

Ускорения, измеряемые акселерометрами, после однократного интегрирования управляют прецессией гироскопов через датчики моментов 1З и 7, а гироскопы через датчики углов 5 и 11 управля­ют стабилизирующими двигателями платформы 6 и 12.

Ускорения самолета, измеренные акселерометром 14 и проин­тегрированные в интеграторе 17, представляют собой путевую скорость по направлению Север — Юг. После второго интегрирова­ния в интеграторе 16 получают путь, пройденный самолетом в этом же направлении. Если известна начальная широта φ₀, то на указа­теле 15 система будет индицировать текущую географическую ши­роту места.

Сигнал, снимаемый с интегратора 4, пропорционален скорости полета самолета по направлению географической параллели, но в эту скорость входит и скорость вращения Земли, которая для текущей широты выражается зависимостью

V_з = ω_з Rcos φ (10.5)

где V₃ —линейная скорость вращения Земли; R — радиус Земли; φ — географическая широта.

В счетно-решающем блоке 8 решается уравнение (10.5) и уже в интегратор 9 поступает сигнал, пропорциональный скорости дви­жения самолета относительно Земли. После второго интегриро­вания и учета начальной долготы λ_о на индикатор 10 поступает значение текущей географической долготы места. Таким образом в инерциальной системе решаются основные уравнения инерциальной навигации:

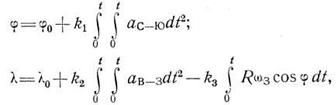(10.6)

где k₁, k₂, k₃ — коэффициенты пропорциональности; а_c-ю, а_в-з — ускорения самолета в направлении Север — Юг и Восток — За­пад соответственно.

Как и все измерительные устройства, инерциальные системы навигации подвержены ошибкам как методическим, так и инстру­ментальным. К методическим ошибкам относят ошибки, вызывае­мые ускорениями Кориолиса, несферичностью Земли и т. д., к ин­струментальным — ошибки элементов, составляющих систему, и ошибки начальной ориентации платформы. Однако точность сов­ременных инерциальных систем достаточно высока и составляет примерно 2 км за час полета; такой точностью обладают зарубеж­ные системы Литтон 51 и Литтон 104.

Инерциальные системы навигации находят все большее приме­нение в гражданской авиации, так как позволяют получать высо­кую точность при решении большого комплекса навигационных и пилотажных задач.