Потенциальная энергия тела и системы тел

Поле как форма материи, осуществляющее силовое взаимодействие между телами. Силовые поля в механике. Потенциальные силы. Потенциальная энергия материальной точки во внешнем силовом потенциальном поле. Нормировка потенциальной энергии. Понятие о силе как градиенте потенциальной энергии. Потенциальная энергия в полях физических сил: однородное поле, центральное поле, гравитационное поле, электростатическое поле, поле сил упругости. Непотенциальность сил трения.

Полем сил называют область пространства, в каждой точке которого на помещенную туда частицу действует сила, закономерно меняющаяся от точки к точке. Примером может служить поле силы тяжести Земли или поле сил сопротивления в потоке жидкости (газа). Если сила в каждой точке силового поля не зависит от времени, то такое поле называют стационарным. Ясно, что силовое поле, стационарное в одной системе отсчета, в другой системе может оказаться и нестационарным. В стационарном силовом поле сила зависит только от положения частицы.

Работа, которую совершают силы поля при перемещении частицы из точки 1 в точку 2, зависит, вообще говоря, от пути. Однако среди стационарных силовых полей имеются такие, в которых эта работа не зависит от пути между точками 1 и 2. Этот класс полей, обладая рядом важнейших свойств, занимает особое место в физике. Рассмотрим свойства таких полей.

Введем определение: стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от формы пути, а зависит только от положения этих точек, называется потенциальным, а сами силы - консервативными.

Если это условие не выполняется, то силовое поле не является потенциальным, а силы поля называют неконсервативными. К числу таких сил принадлежит, например, сила трения, так как работа этой силы зависит в общем случае от пути.

Покажем, что в потенциальном поле работа сил поля на любом замкнутом пути равна нулю.Действительно, любой замкнутый путь (рис. 6.1) можно разбить произвольно на две части: 1а2 и 2b1. Так как поле

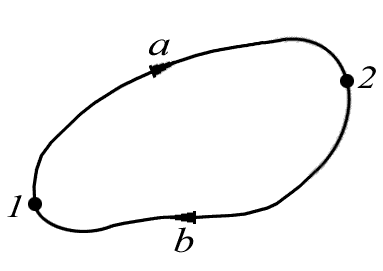Рис. 6.1. Работа в потенциальном поле сил

потенциально, то, по условию 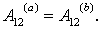С другой стороны, очевидно, что 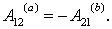Поэтому

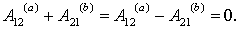
что и требовалось доказать.

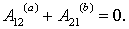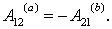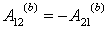Наоборот, если работа сил поля на любом замкнутом пути равна нулю, то и работа этих сил на пути между произвольными точками 1 и 2 от формы пути не зависит, т. е. поле потенциально. Для доказательства выберем два произвольных пути: 1а2 и 1b2 (рис. 6.1). Составим из них замкнутый путь 1a2b1. Работа на этом замкнутом пути по условию равна нулю, т. е. Отсюда Но , поэтому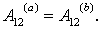

Таким образом, равенство нулю работы сил поля на любом замкнутом пути есть необходимое и достаточное условие независимости работы от формы пути, и может считаться отличительным признаком любого потенциального поля сил.

Рассмотрим важный случай поля центральных сил. Всякое силовое поле вызывается действием определенных тел. Сила, действующая на частицу А в таком поле, обусловлена взаимодействием этой частицы с данными телами. Если силы, зависят только от расстояния между взаимодействующими частицами и направлены по прямой, соединяющей эти частицы, отих называют центральными. Такими примерами служат силы гравитационные, кулоновские и упругие.

Центральную силу, действующую на частицуА со стороны частицы В, можно представить в общем виде:

,

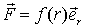(6.1)

где 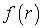-функция, зависящая при данном характере взаимодействия только от r - расстояния между частицами; 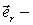единичный вектор, задающий направление радиус-вектора частицы А относительно частицы В (рис.6).

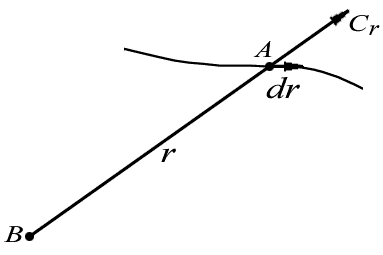Рис. 6.2 Работа в поле центральных сил

Докажем, что всякое стационарное поле центральных сил потенциально. Для этого найдем работу центральных сил в случае, когда силовое поле вызвано наличием одной неподвижной частицы B, а затем обобщим результат на произвольный случай. Элементарная работа силы

на перемещении 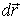есть 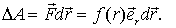Так как 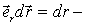проекция вектора 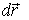на вектор 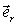, или на соответствующий радиус-вектор 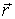(рис. 6.2), то 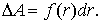Работа же этой силы на произвольном пути от точки 1 до точки 2

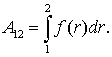
Полученное выражение зависит, очевидно, только от вида функции 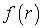, т. е. от характера взаимодействия и от значений и 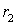- начального и конечного расстояний между частицами A и B. От формы пути оно никак не зависит. Это и означает, что данное силовое поле потенциально.

Обобщим полученный результат на стационарное силовое поле, вызванное наличием совокупности неподвижных частиц, действующих на частицу A с силами 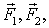.., каждая из которых является центральной. В этом случае работа результирующей силы при перемещении частицы A из одной точки в другую равна алгебраической сумме работ отдельных сил. А так как работа каждой из этих сил не зависит от формы пути, то и работа результирующей силы от нее также не зависит. Таким образом, действительно, любое стационарное поле центральных сил потенциально.

Введем понятие потенциальной энергии частицы в поле. То, что работа сил потенциального поля зависит только от начального и конечного положений частицы, дает возможность ввести чрезвычайно важное понятие потенциальной энергии.

Представим себе, что мы перемещаем частицу в потенциальном поле сил из разных точек P в фиксированную точку O. Так как работа сил поля не зависит от формы пути, то остается зависимость ее только от положения точки P (при фиксированной точке O ). А это значит, что данная работа будет некоторой функцией радиус-вектора r точки P.

Обозначив эту функцию 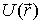, запишем

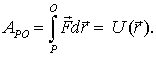(6.2)

Функцию 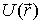называют потенциальной энергией частицы в данном поле.

Потенциальная энергия (U)— механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними. Потенциальная энергия системы является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.

Теперь найдем работу сил поля при перемещении частицы из точки 1 в точку 2 (рис.6.3). Так как работа не зависит от пути, выберем путь,

Рис. 6.3. Введение понятия потенциальной энергии

проходящий через точку O. Тогда работа на пути 1O2 может быть представлена в виде

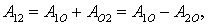
или с учетом (6.2)

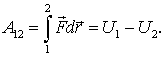(6.3)

Выражение, стоящее справа, есть убыль потенциальной энергии, т. е. разность значений потенциальной энергии частицы в начальной и конечной точках пути. Таким образом, работа сил поля на пути 1-2 равна убыли потенциальной энергии частицы в данном поле.

Изменение какой-либо произвольной физической величины X можно характеризовать либо ее приращением, либо убылью. Приращением величины X называют разность конечного 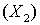и начального 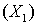значений этой величины:

Приращение .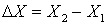

Убылью величины X называют разность ее начального 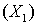и конечного 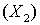значений:

Убыль ,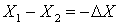

т. е. убыль величины X равна ее приращению, взятому с обратным знаком. Приращение и убыль - величины алгебраические: если 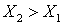, то приращение положительно, а убыль отрицательна, и наоборот.

Очевидно, частице, находящейся в точке O поля, всегда можно приписать любое заранее выбранное значение потенциальной энергии. Это соответствует тому обстоятельству, что путем измерения работы может быть определена лишь разность потенциальных энергий в двух точках поля, но не ее абсолютное значение. Однако как только фиксирована потенциальная энергия в какой-либо точке, значения ее во всех остальных точках поля однозначно определяются формулой (6.3).

Формула (6.3) дает возможность найти выражение 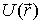для любого потенциального ноля сил. Для этого достаточно вычислить работу, совершаемую силами поля на любом пути между двумя точками, и представить ее в виде убыли некоторой функции, которая и есть потенциальная энергия .

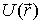Именно так и было сделано при вычислении работы в полях упругой и гравитационной (кулоновской) сил, а также в однородном поле тяжести. Потенциальная энергия частицы в данных силовых нолях имеет следующий вид:

1) в поле упругой силы

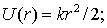(6.4)

2) в поле точечной массы (заряда)

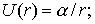(6.5)

где 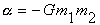для гравитационного взаимодействия и 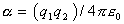для кулоновского взаимодействия;

3) в однородном поле сил тяжести

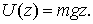(6.6)

Еще раз подчеркнем, что потенциальная энергия 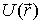- это функция, которая определяется с точностью до прибавления некоторой произвольной постоянной. Это обстоятельство, однако, совершенно несущественно, ибо во все формулы входит только разность значений 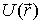в двух положениях частицы. Поэтому произвольная постоянная, одинаковая для всех точек поля, выпадает. В связи с этим ее обычно опускают, что и сделано в трех предыдущих выражениях.

Отметим еще одно важное обстоятельство. Потенциальную энергию следует относить не к частице, а к системе взаимодействующих между собой частицы и тел, вызывающих силовое поле. При данном характере взаимодействия потенциальная энергия взаимодействия частицы с данными телами зависит только от положения частицы относительно этих тел.

Определим связь потенциальной энергии и силы поля. Взаимодействие частицы с окружающими телами можно описывать двумя способами: с помощью сил или с помощью потенциальной энергии. В классической механике оба способа используют одинаково широко. Однако первый способ обладает несколько большей общностью, ибо он применим и к таким силам, для которых нельзя ввести потенциальную энергию (например, к силам трения). Второй же способ применим только в случае консервативных сил.

Наша задача - установить связь между потенциальной энергией и силой поля, точнее, определить поле сил 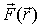по заданной потенциальной энергии 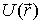как функции положения частицы в поле.

Ранее было показано, что при перемещении частицы из одной точки потенциального поля в другую работа, которую производят силы поля, может быть представлена как убыль потенциальной энергии частицы, т. е. 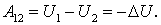Это относится и к элементарному перемещению 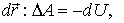или

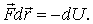(6.7)

Учитывая, что 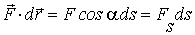, где 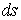- элементарный путь, перепишем уравнение (6.7) в форме

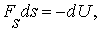
где 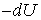- это убыль потенциальной энергии в направлении перемещения 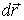. Отсюда

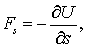(6.8)

т. е. проекция силы поля - вектора 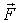- в данной точке на направление перемещения 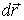равна с обратным знаком производной потенциальной энергии 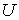по данному направлению. Символ 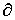- частнойпроизводной - подчеркивает, что производная берется по определенномунаправлению.

Перемещение 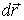мы можем взять в любом направлении, в частности вдоль координатных осей х, у, z. Если перемещение 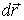, например, параллельно оси х, то его можно представить так: 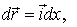где 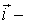орт оси 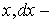приращение координаты. x. Тогда paбота силы 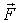на перемещении 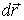, параллельном оси x,

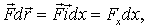
где 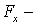проекция вектора 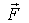на орт 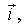а не на перемещение 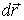, как в случае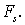

Подставив последнее выражение в уравнение (6.8), получим

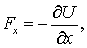
где символ частной производной означает, что потенциальная энергия 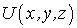при дифференцировании должна рассматриваться как функция одного аргумента х, остальные же аргументы должны оставаться при этом постоянными. Ясно, что для проекци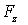й и 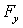уравнения будут аналогичны уравнению для .

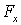Итак, взяв с обратными знаками частные производные функции U по х, у и z, мы найдем проекци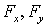и и 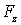вектора 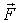на орты 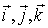. Отсюда легко найти и сам вектор: 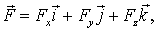или

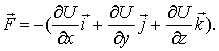
Величину, стоящую в скобках, называют градиентом скалярной функцииU и обозначают 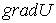или 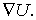Мы будем пользоваться вторым, более удобным, обозначением, где значок 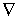"набла" означает символический векторный оператор

.

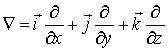Поэтому 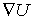формально можно рассматривать как произведение символического вектора 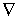на скаляр .

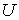Таким образом, связь между силой поля и потенциальной энергией как функцией координат можно представить в следующем компактном виде:

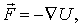(6.9)

т. е. сила поля 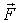равна со знаком минус градиенту потенциальной энергиичастицы в данной точке поля. Последняя формула дает возможность, зная функцию 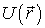, восстановить поле сил .

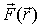Пример. Потенциальная энергия частицы в некотором поле имеет вид:

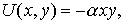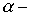а) где постоянная;

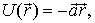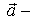б) где постоянный вектор, радиус-вектор точки поля

Найдем соответствующее каждому случаю поле сил:

а)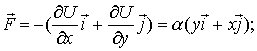

б) представим сначала функцию U в виде 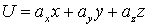; тогда

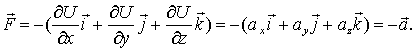
Смысл градиента станет нагляднее и яснее, если ввести понятие эквипотенциальной поверхности- поверхности, во всех точках которой потенциальная энергия U имеет одно и то же значение. Ясно, что каждому значению U соответствует своя эквипотенциальная поверхность.

Из формулы (6.9) следует, что проекция вектора 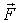на любое направление, касательное к эквипотенциальной поверхности в данной точке, равна нулю. Это значит, что вектор 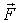нормален эквипотенциальной поверхности в данной точке. Далее, возьмем перемещение 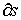в сторону уменьшения U, тогда U меньше 0, и, согласно (6.8), 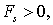т.е. вектор 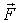направлен в сторону уменьшения U. А так как 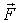противоположен по направлению вектору 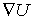, то мы приходим к выводу, что градиент U - это вектор, направленный по нормали к эквипотенциальной поверхности в сторону возрастания потенциальной энергии U.

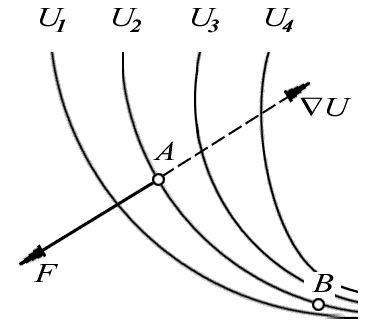Рис. 6.4. Эквипотенциальные поверхности и направление силы

Сказанное поясняет рис. 6.4, относящийся к двумерному случаю. На нем изображена система эквипотенциалей , a также градиент потенциальной энергии U и соответствующий вектор силы 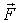в точке А поля. Полезно подумать, какими будут векторы этих двух величин, например, в точке В данного поля.

В заключение заметим, что можно говорить о градиенте не только функции U, но и любой другой скалярной функции координат. Понятие градиента широко используется в самых различных разделах физики, особенно в теории электромагнетизма.

Рассмотрим понятие поля сил. Опыт показывает, что в случае гравитационных и электростатических взаимодействий сила 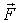, действующая на частицу А со стороны окружающих тел (системы В), пропорциональна массе (или заряду) частицы А Другими словами, сила 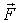может быть представлена в виде произведения двух величии:

,

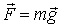(6.10)

где m-масса (или заряд) частицы A, 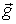- некоторый вектор (для гравитационных сил вблизи поверхности Земли он совпадает с вектором ускорения свободного падения), зависящий как от положения частицы А, так и от свойств окружающих тел - системы В.

Такое представление силы открывает возможность иной физической интерпретации взаимодействия, связанной с понятием поля. А именно: в этом случае говорят, что система В создает в окружающем пространстве поле, характеризуемое вектором 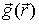. По-другому можно сказать, .что в каждой точке пространства система В - источник поля - создает такие условия (вектор 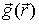), при которых частица, помещенная в эти точки, испытывает действие силы (6.10). Причем считают, что поле (вектор 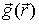) существует безотносительно к тому, есть ли в нем частица А или нет. При рассмотрении стационарных случаев, понятие поля может рассматриваться как чисто условное (формальное), введенное лишь для удобства описания явлений. Однако при переходе к переменным полям выясняется, что понятие поля имеет глубокий физический смысл: поле есть физическая реальность.

Вектор 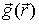называют напряженностью поля. Одно из важнейших свойств полей заключается в том, что поле, образованное несколькими источниками, равно сумме полей, созданных каждым из них. Точнее, напряженность G результирующего поля в произвольной точке

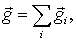(6.11)

где 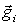- напряженность поля соответствующего источника в этой же точке. Эта формула выражает так называемый принцип суперпозиции(или наложения) полей, который является отражением опытных фактов и дополняет законы механики.

Обратимся теперь к потенциальной энергии частицы. Согласно (6.10), формулу (6.7) можно записать так: 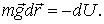Поделив обе части на т и обозначив 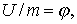получим

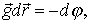(6.12)

или

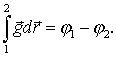(6.13)

Функцию 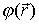называют потенциалом поля в точке с радиус-вектором .

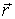Формула (6.13) дает возможность, в частности, найти потенциал любого гравитационного и электростатического полей. Для этого достаточно вычислить интеграл по произвольному пути между точками 1 и 2 и представить затем полученное выражение в виде убыли некоторой функции, которая и есть потенциал 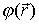. Так, потенциалы гравитационного ноля точечной массы т и кулоновского поля точечного заряда q определяются, согласно (6.5), формулами

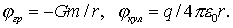(6.14)

Заметим, что потенциал 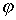, как и потенциальная энергия, может быть определен только с точностью до прибавления некоторой произвольной постоянной, также совершенно несущественной. Поэтому ее обычно опускают, полагая равной нулю.

Итак, поле можно описывать или в векторном виде 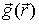, или в скалярном 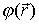. Оба способа эквиваленты. Практически же оказывается, что второй способ описания поля с помощью потенциала 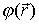в большинстве случаев значительно удобнее. Этому есть несколько причин.

1. Зная 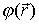, можно немедленно вычислить потенциальную энергию U и работу сил поля A:

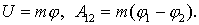(6.15)

2. Вместо трех компонент векторной функции 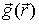проще задавать скалярную функцию .

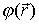3. Когда поле создается многими источниками, потенциал 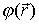рассчитывать легче, чем вектор 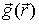: потенциалы - скалярные величины, их можно просто складывать, не заботясь о напрвлении сил. Действительно, согласно (6.11) и (6.12), 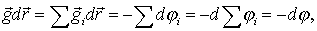то есть

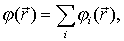(6.16)

где 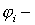потенциал, создаваемый 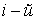частицей в данной точке поля.

4. И наконец, зная функцию 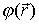, можно легко восстановить поле 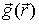- как антиградиент потенциала :

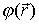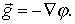(6.17)

Эта формула непосредственно следует из (6.9).