Потенциальная энергия во внешнем поле сил. связь между силой и потенциальной энергией. градиент скалярной функции

Из выражения (4.9) следует, что работа равна приращению потенциальной функции, и эта работа идет на приращение кинетической энергии частицы, как показывает (4.5). Таким образом,

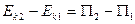. (4.11)

Перейдем от функции 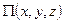к функции 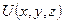, связанной с 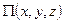соотношением

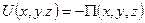. (4.12)

Тогда из (4.11) получаем: 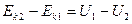, или .

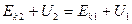Полученный результат означает, что величина 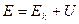для частицы, находящейся в поле консервативных сил, остается постоянной, т.е. является интегралом движения. Функция 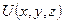называется потенциальной энергией частицы во внешнем поле сил. Таким образом, потенциальная энергия характеризует взаимодействие частицы с полем сил и зависит от положения частицы в этом поле, т.е. от координат.

Величину 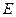, равную сумме кинетической и потенциальной энергии, называют полной механической энергией частицы.

Из выражения (4.9) с учетом (4.12) получаем

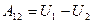
-работа, совершаемая над частицей силами консервативного поля, равна убыли потенциальной энергии частицы, т.е. работа совершается за счет запаса потенциальной энергии. Работа, совершаемая консервативными силами при переходе системы из некотоpого положения в нулевое, называется потенциальной энергией U системы в этом положении.

Выражение (4.7) с учетом (4.12) принимает вид

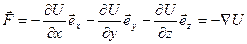
–сила, действующая на частицу в стационарном поле сил, равна градиенту потенциальной энергии частицы в этом поле, взятому с обратным знаком.

Пусть на частицу, кроме сил стационарного потенциального поля, действует также неконсервативная сила 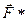. Тогда при переходе частицы из точки 1 в точку 2 над ней будет совершаться работа 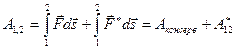,где 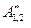- работа неконсервативной силы. Работа консервативных сил равна убыли потенциальной энергии. Тогда

.

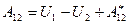Суммарная работа всех приложенных к частице сил идет на приращение ее кинетической энерги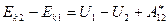и: , или

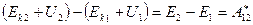
-работа неконсервативных сил затрачивается на приращение полной механической энергии частицы.

Потенциальная энергия, как и потенциальная функция, определяется с точностью до произвольной аддитивной постоянной. Однако, это не имеет значения, так как во все функции входит либо разность значений потенциальной энергии, либо ее производные. В каждой конкретной задаче выбирается начало отсчета потенциальной энергии, от которого ведут расчет энергии в других положениях. Поэтому 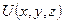может иметь как положительные, так и отрицательные значения.

Конкретный вид функции 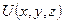зависит от характера силового поля. В поле тяжести 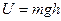, где 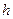отсчитывается от произвольного уровня.

Рассмотрим систему, состоящую из 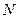невзаимодействующих между собой частиц, находящихся в поле консервативных сил. Каждая из частиц обладает кинетической 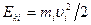и потенциальной энергией 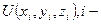номер частицы, тогда для каждой частицы можно записать

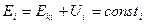
Просуммировав эти выражения для всех частиц, получаем

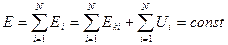
- полная механическая энергия системы невзаимодействующих частиц, на которые действуют только консервативные силы, остается постоянной.

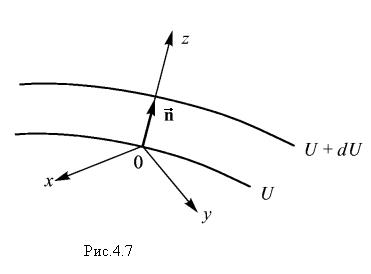
Для выяснения геометрического смысла градиента полезно ввести эквипотенциальные поверхности, то есть такие поверхности, на которых скалярная функция U остается постоянной: U(x,y,z) = const.

Пусть U — одна из таких поверхностей, и пусть она проходит через точку пространства O, в которой определяется градиент (pис. 4.7). Поместим в этой точке начало координат. Ось Z направим по нормали к поверхности ( 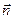— единичный орт нормали), а оси X и Y лежат в плоскости, касательной к поверхности в точке O. Поэтому в первом приближении вдоль осей x и y функция U не изменяется: 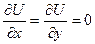. Следовательно, 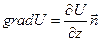поскольку в нашем случае 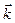= . Если U возрастает в направлении оси Z, то ∂ U/ ∂ z> 0 и, следовательно, градиент направлен по нормали к эквипотенциальной поверхности в сторону возрастания потенциальной энергии. Очевидно, что в этом направлении потенциальная энергия изменяется наиболее быстро: 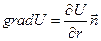. Таким образом, мы приходим к выводу, что градиент скалярной функции U есть вектор, направленный по нормали к эквипотенциальной поверхности U(x,y,z) = const в сторону возрастания функции U. Его длина численно равна производной от U по нормали к эквипотенциальной поверхности. Это определение, как говорят, инвариантно. Оно не завиcит от выбора системы координат.

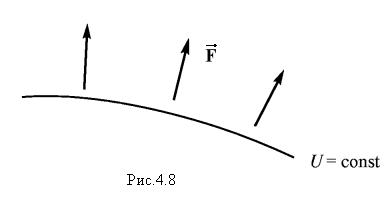
Наряду с эквипотенциальной поверхностью через каждую точку пространства можно провести так называемую силовую линию. Направление касательной к ней в каждой точке совпадает с направлением силы, действующей на частицу в этой точке. Очевидно, что силовые линии и эквипотенциальные поверхности взаимно ортогональны друг другу (pис. 4.8).

Пользуясь понятием градиента, втоpой закон Ньютона при движении одной материальной точки в силовом поле можно представить в виде .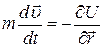

Покажем теперь, как из этого уравнения следует закон сохранения энергии. Умножим для этого правую и левую части уравнения скалярно на скорость частицы : .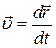

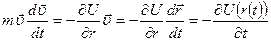Выражение слева можно переписать через производную по времени от кинетической энергии частицы 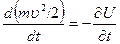или, перенося все в левую часть, 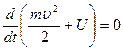и 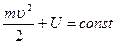— получаем закон сохранения энергии. Заметим, что при выводе здесь было важно, чтобы потенциальная энергия частицы не зависела бы явно от времени t (то есть как) 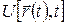. Зависимость от времени входила в потенциальную энергию лишь неявно, через зависимость от времени радиус-вектора частицы 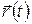(то есть как ).

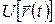ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ

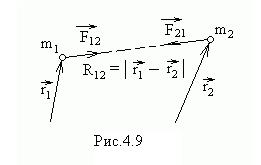
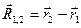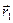Рассмотрим замкнутую систему, состоящую из двух взаимодействующих частиц (рис.4.9). Введем вектор , где и 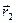- радиус-векторы частиц. Расстояние между частицами равно модулю этого вектора. Будем считать, что силы взаимодействия частиц 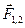и 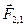зависят только от расстояния 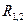между ними, и направлены вдоль прямой, соединяющей частицы:

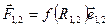, (4.13)

где 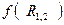- некоторая функция 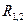, 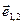- орт вектора 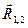(рис.4.10). По третьему закону Ньютона 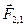= - 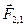. Уравнения движения

частиц

.

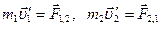Умножим первое уравнение на 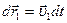, второе – на 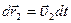и сложим:

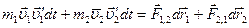. (4.14)

Левая часть этого выражения представляет собой приращение кинетической энергии системы за время 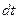, а правая часть – работу внутренних сил за то же время:

.

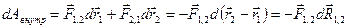Подставив в это выражение формулу (4.13), получаем

.

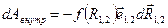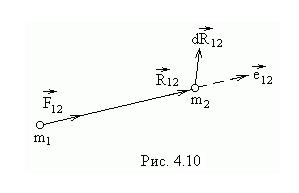
Из рис.4.10 видно, что скалярное произведение 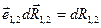равно приращению расстояния между частицами. Тогда

.

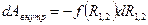Выражение 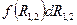есть приращение некоторой функции от :

.

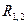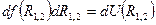Следовательно, 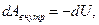и выражение (4.14) можно представить в виде:

.

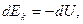или 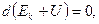таким образом, величина 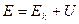для замкнутой системы сохраняется. Функция 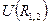представляет собой потенциальную энергию взаимодействия. Она зависит от расстояния между частицами. Работа внутренних сил

Т.е. не зависит от путей, по которым перемещались частицы, а определяется только начальными и конечными расстояниями между частицами. Таким образом, силы взаимодействия вида (4.13) являются консервативными.