Относительность механического движения. Системы отсчета
Раздел 1. Механика
Механическое движение — это изменение положения тел в пространстве относительно друг друга с течением времени.
Механическое движение может быть прямолинейным или криволинейным, равномерным или неравномерным.
Материальная точка — это тело, размеры и форму которого при решении задачи можно не учитывать.
Условия, при выполнении которых тело можно считать материальной точкой:
1. если его размеры малы по сравнению с расстоянием, которое оно проходит.
2. если оно движется поступательно.
Что такое поступательное движение?
Тело движется поступательно, если все его точки движутся одинаково.
Тело движется поступательно, если прямая, проведенная через две точки этого тела, …
при его перемещении смещается параллельно своему первоначальному положению.
Система отсчета (СО)
Тело отсчета, связанная с ним система координат и часы для отсчета времени движения образуют систему отсчета.
Тело отсчета — это тело, относительно которого определяется положение других (движущихся) тел.
Относительность движения
Человек идет по вагону против движения поезда (рис. 1). Скорость поезда относительно поверхности земли равна 20 м/с, а скорость человека относительно вагона равна 1 м/с. Определите, с какой скоростью и в каком направлении движется человек относительно поверхности земли.
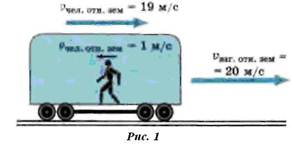
Будем рассуждать так. Если бы человек не шел по вагону, то он переместился бы вместе с поездом на расстояние, равное 20 м. Но за это же время он прошел расстояние, равное 1 м, против хода поезда. Поэтому за время, равное 1 с, он сместился относительно поверхности земли только на 19 м в направлении движения поезда. Значит, скорость человека относительно поверхности земли равна 19 м/с и направлена в ту же сторону, что и скорость поезда. Таким образом, в системе отсчета, связанной с поездом, человек движется со скоростью 1 м/с, а в системе отсчета, связанной с каким-либо телом на поверхности земли, — со скоростью 19 м/с, причем направлены эти скорости в противоположные стороны. Мы видим, что скорость относительна, т. е. скорость одного и того же тела в разных системах отсчета может быть различной как по числовому значению, так и по направлению.
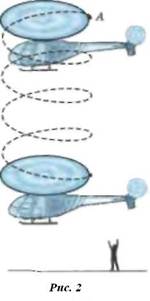
Теперь обратимся к другому примеру. Представьте вертолет, вертикально опускающийся на землю. Относительно вертолета любая точки винта, например точка А(рис. 2), будет все время двигаться по окружности, которая на рисунке изображена сплошной линией. Для наблюдателя, находящегося на земле, та же самая точка будет двигаться по винтовой траектории (штриховая линия). Из этого примера ясно, что траектория движения тоже относительна,т. е. траектория движения одного и того же тела может быть различной в разных системах отсчета.
Отсюда следует, что и путь является величиной относительной,ведь путь — это сумма длин всех участков траектории, пройденных телом за рассматриваемый промежуток времени. Это особенно наглядно проявляется в тех случаях, когда физическое тело движется в одной системе отсчета и покоится в другой. Например, человек, сидящий в движущемся поезде, проходит определенный путь s в системе, связанной с Землей, а в системе отсчета, связанной с поездом, его путь равен нулю.
Таким образом, относительностьдвижения,проявляется втом, что скорость, траектория, путь инекоторые другие характеристики движения относительны, т. е. они могут быть различны в разных системах отсчета.
| Относительность механического движения. | |
| 1. Механическое движение можно наблюдать только относительно других тел. Обнаружить изменение положения тела, если не с чем сравнивать невозможно. 2. В различных системах отсчета физические величины (скорость, ускорение, перемещение и т.д.), характеризующие движение одного и того же тела, могут быть различными. 3. Характер движения, траектория движения и т.п. различны в разных системах отсчета для одного и того же тела. | |
Пусть две СО движутся друг относительно друга с постоянной скоростью 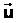 . Положение точки А в неподвижной системе К задано вектором . Положение точки А в неподвижной системе К задано вектором 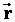 , а в движущейся системе К1 — вектором , а в движущейся системе К1 — вектором 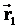 . Из чертежа видим, что . Из чертежа видим, что 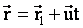 . Это уравнение позволяет переходить из одной СО в другую. При этом мы считаем, что время течет в обеих СО одинаково. Будем условно называть систему К неподвижной, а систему К1 — движущейся. . Это уравнение позволяет переходить из одной СО в другую. При этом мы считаем, что время течет в обеих СО одинаково. Будем условно называть систему К неподвижной, а систему К1 — движущейся. | 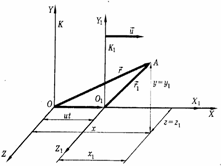 |
Тогда для случая, когда координатыy и z не меняются, получим: 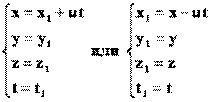 — преобразования Галилея. — преобразования Галилея. | |
Из этих уравнений следует: — расстояние между двумя точками абсолютно, т.е. не зависит от выбора СО. Пусть в неподвижной СО координаты точекx и x’, а в подвижной соответственно x1 и x1‘. Тогда 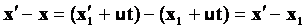 ; ; 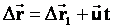 Разделим правую и левую часть уравнения на промежуток времени, в течение которого шло перемещение. Получим: Разделим правую и левую часть уравнения на промежуток времени, в течение которого шло перемещение. Получим: 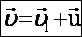 —закон сложения скоростей.Здесь скорость точки относительно неподвижной СО равна векторной сумме скорости точки относительно подвижной СО и скорости самой подвижной СО относительно неподвижной. —закон сложения скоростей.Здесь скорость точки относительно неподвижной СО равна векторной сумме скорости точки относительно подвижной СО и скорости самой подвижной СО относительно неподвижной. | 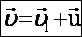 |
| Скорость подвижной СО относительно неподвижной наз. переносной скоростью. | |
| При решении задач часто бывает удобно принимать одно из движущихся относительно Земли тел за неподвижное. Тогда скорость Земли в этой СОбудет равна по величине и противоположна по направлению скорости данного тела. | |
Если скоростиv1 и u сонаправлены, то их проекции складываются, если противоположно направлены (тела удаляются) – вычитаются. Если скорости направлены под прямым углом — 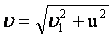 если угол произвольный, то необходимо пользоваться теоремой косинусов: если угол произвольный, то необходимо пользоваться теоремой косинусов: 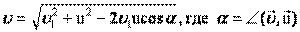 . . | |
| Эти выводы справедливы для скоростей много меньших скорости света в вакууме (3.108м/с). |
