Условие неразрывности для несжимаемой жидкости
Выберем сечения 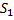 и
и  настолько маленькими, то есть трубку тока настолько тонкой, что в каждом её сечении скорость (
настолько маленькими, то есть трубку тока настолько тонкой, что в каждом её сечении скорость (  ) можно считать одинаковой. Тогда можно вычислить количество жидкости, перетекающей за определённой время через поверхность
) можно считать одинаковой. Тогда можно вычислить количество жидкости, перетекающей за определённой время через поверхность 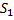 и
и  .
.
Масса, которая перешла за время 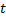 через поверхность
через поверхность 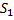 :
: 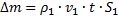 , где
, где 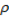 – плотность жидкости.
– плотность жидкости.
Также можно вычислить массу, которая перешла через поверхность  за время t:
за время t: 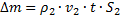 .
.
Так как количество вещества, которое втекло в объём и которое из него вытекло, одинаково, то 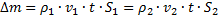 .
.
Если рассматривать несжимаемые жидкости, то плотность вещества в сечении 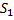 совпадает с плотностью вещества в сечении
совпадает с плотностью вещества в сечении  .
.
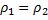
Следовательно, получаем следующее соотношение: 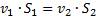 .
.
То есть для несжимаемой жидкости, произведение скорости на площадь поперечного сечения трубки тока одинаково вдоль всей трубки: 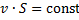 – условие неразрывности. Это означает, что, чем меньше поперечное сечение, тем больше скорость.
– условие неразрывности. Это означает, что, чем меньше поперечное сечение, тем больше скорость.
Уравнение Бернулли
Динамика движения реальной жидкости очень сложная, однако в некоторых случаях можно пренебречь вязкостью жидкости, то есть наличием трения между различными слоями жидкости. В этом случае при движении жидкости не выделяется тепло, то есть сохраняется механическая энергия. Закон движения такой идеальной несжимаемой жидкости без вязкости называется уравнением Бернулли, которое полностью основано на законе сохранения механической энергии.
Рассмотрим энергетические соотношения при движении идеальной несжимаемой жидкости. Выделяем некоторую трубку тока, ограниченную сечениями 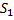 и
и  (см. рис. 3). За некоторое время
(см. рис. 3). За некоторое время 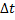 масса жидкости, заключённой между сечениями
масса жидкости, заключённой между сечениями 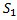 и
и  , сместится. Сечение
, сместится. Сечение  перейдёт в сечение
перейдёт в сечение 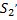 , а
, а 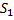 – в
– в 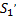 .
.
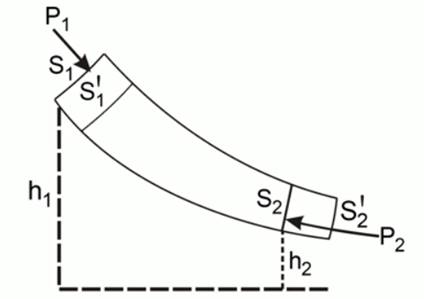
Рис. 3. Трубка тока
Рассматриваем не только очень маленькие сечения трубки тока, но и очень маленькие промежутки времени, в течение которых сечения сместятся на очень маленькую величину. Будем пренебрегать изменением площади сечений, изменением высоты, скорости и давления на этих сечениях. С учётом этих данных рассчитаем работу внешних сил над данным объёмом жидкости. Эта работа складывается из таких работ:
1) Внешняя часть жидкости давит на сечение 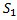 с силой
с силой 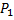 , поэтому совершает работу при перемещении этого сечения.
, поэтому совершает работу при перемещении этого сечения.
2) Внешняя часть жидкости давит на сечение  с силой
с силой 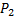 и совершает отрицательную работу при перемещении этого сечения.
и совершает отрицательную работу при перемещении этого сечения.
Также меняется кинетическая и потенциальная энергия жидкости.
Для того чтобы легче было это понять, рассмотрим объём жидкости, заключённый между сечениями 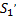 и
и  . Энергия, масса, скорость, давление и остальные характеристики этого объёма не изменились в силу стационарности движения. Поэтому вся работа внешних сил привела к тому, что энергия части жидкости между
. Энергия, масса, скорость, давление и остальные характеристики этого объёма не изменились в силу стационарности движения. Поэтому вся работа внешних сил привела к тому, что энергия части жидкости между 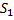 и
и 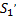 переместилась в часть между
переместилась в часть между 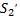 и
и  с ниже посчитанными изменениями:
с ниже посчитанными изменениями:
-работа внешних сил в верхней части трубки: 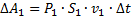 ;
;
-работа внешних сил в нижней части трубки ( 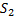 сдвигается в сторону противоположную силе давления, поэтому работа имеет знак минус):
сдвигается в сторону противоположную силе давления, поэтому работа имеет знак минус): 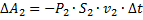 ;
;
-суммарная работа, произведённая над объёмом, передвинувшимся за время 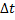 :
: 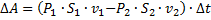 .
.
Вычислим изменение энергии рассмотренного отрезка трубки тока (изменение энергии части жидкости между 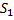 и
и 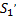 по сравнению с энергией между
по сравнению с энергией между 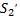 и
и  ), для этого из энергии конечной отнимаем энергию начальную.
), для этого из энергии конечной отнимаем энергию начальную.
Изменение потенциальной энергии (потенциальная энергия – это масса (масса – это плотность ( 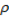 ), умноженная на объём, а объём в данном случае – это поперечное сечение на длину участка между
), умноженная на объём, а объём в данном случае – это поперечное сечение на длину участка между 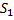 и
и 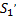 или
или 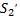 и
и  (
( 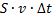 )), умноженная на ускорение свободного падения (
)), умноженная на ускорение свободного падения ( 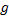 ) и высоту этого участка над некоторым нулевым уровнем):
) и высоту этого участка над некоторым нулевым уровнем):
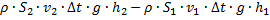 .
.
Изменение кинетической энергии (масса, умноженная на квадрат скорости и делённая на два): 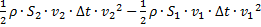 .
.
Изменение энергии в соответствии с законом сохранения энергии равно работе внешних сил.
Приравниваем эти величины и переносим слагаемые с одинаковыми индексами в одну сторону. Сократив 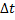 ,
, 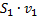 и
и 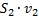 (согласно условию неразрывности
(согласно условию неразрывности 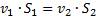 ), получаем окончательный результат:
), получаем окончательный результат: 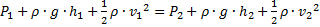 .
.
Сечения 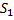 и
и  были выбраны произвольно, поэтому уравнение можно записать в таком виде:
были выбраны произвольно, поэтому уравнение можно записать в таком виде: 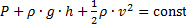 .
.
Мы получили уравнение Бернулли. Это уравнение утверждает, что сумма физических величин ( 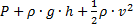 ) постоянна вдоль очень узкой трубки тока. В математическом смысле следует устремить сечение этой трубки к нулю, то есть получим линию тока. Следовательно,
) постоянна вдоль очень узкой трубки тока. В математическом смысле следует устремить сечение этой трубки к нулю, то есть получим линию тока. Следовательно, 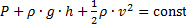 вдоль любой линии тока.
вдоль любой линии тока.
