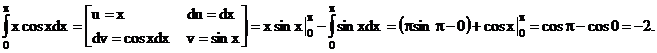Вопрос 3. Определенный интеграл как функция верхнего предела

Если функция y = f(x) интегрируема на отрезке [a;b], то она интегрируема и на любом меньшем отрезке, т.е. для "xÎ[a;b] существует интеграл

(4)

Для того чтобы не смешивать обозначения предела и переменной интегрирования, обозначим переменную интегрирования через t. Тогда интеграл (4) запишется в виде Величина этого интеграла является функцией верхнего предела х и обозначается Ф(х):

. (5)

Функция Ф(х) называется интегралом с переменным верхним пределом.

Рассмотрим некоторые свойства функции Ф(х).

Т.3.1.(непрерывность функции Ф(х))

Если функция f(x) непрерывна на отрезке [a;b], то функция Ф(x) будет так же непрерывна на отрезке [a;b].

Т.3.2.(дифференцирование функции Ф(х))

Если функция f(x) непрерывна на отрезке [a;b], то функция Ф(x) дифференцируема в любой внутренней точке х этого отрезка, причем справедливо равенство

.

Следствие

Если функция f(x) непрерывна на отрезке [a;b], то для этой функции существует первообразная на данном отрезке, причем функция Ф(x) - интеграл с переменным верхним пределом – является первообразной для функции f(x).

Так как всякая другая первообразная для функции f(x) отличается от Ф(x) только на постоянное слагаемое, то можно установить связь между неопределенным и определенным интегралами:

,

где С – произвольная постоянная.

Вопрос 4. Вычисление определенного интеграла. Формула Ньютона-Лейбница

Вычисление определенных интегралов методом, основанным на определении интеграла как предела интегральных сумм, как правило, связано с большими трудностями. Существует более удобный метод вычисления определенных интегралов, который основан на установленной связи между неопределенным и определенным интегралами.

Т.4.1. Если функция f(x) непрерывна на отрезке [a;b] и F(x) - любая первообразная для функции f(x) на [a;b], то справедлива формула

. (6)

Формула (6) называется формулой Ньютона – Лейбница.

Если ввести обозначение то формулу Ньютона-Лейбница (6) можно переписать в виде

.

Формула Ньютона – Лейбница дает удобный способ вычисления определенных интегралов. Чтобы вычислить определенный интеграл необходимо найти любую первообразную функцию F(x) для f(x) и взять разность F(b) ‒ F(a) на концах отрезка [a;b].

Пример

Вопрос 5. Замена переменной и интегрирование по частям в определенном интеграле

Метод замены переменной

При вычислении определенных интегралов широко используется метод подстановки или метод замены переменной.

Т.5.1. (замена переменной в определенном интеграле)

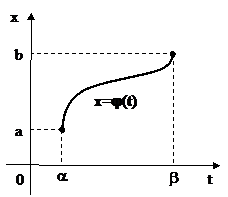
Пусть функция y = f(x) непрерывна на отрезке [a;b]. Тогда, если:

1)функция x = j(t) и ее производная x′ = j′(t) непрерывны на отрезке [a;b];

2)множеством значений функции x = j(t) является отрезок [a;b];

3)j(a) = a, j(b) = b,

то справедлива формула замены переменной в определенном интеграле:

.

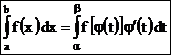Замечание

1. При вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется.

2. Часто вместо подстановки x = j(t) применяют подстановку t = g(x).

3. При использовании формулы необходимо проверять выполнение перечисленных в теореме условий. Если эти условия нарушаются, то может быть получен и неверный результат.

Пример. Вычислить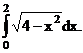

Решение

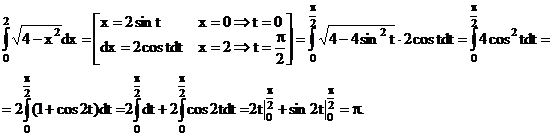
Интегрирование по частям

Т.5.2. (интегрирование по частям в определенном интеграле)

Если функции u = u(x) и v = v(x) имеют непрерывные производные на отрезке [a;b], то справедлива формула интегрирования по частям в определенном интеграле:

.

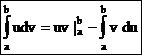Пример. Вычислить интеграл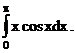

Решение