Первое основное энергетическое состояние атома водорода
Рассмотрим основные виды энергии, определяющие баланс силового взаимодействия – электрическую энергию притяжения электрона к ядру и энергию вращательного механического движения электрона, движущегося по орбите. Именно эти две энергии определяют основное устойчивое энергетическое состояние электрона в атоме водорода на первой орбите (вне зависимости от того, вращается электрон вокруг своей оси, или нет), а их сумма должна быть примерно равна энергии связи, которая в атоме водорода равна энергии его ионизации, WiH:
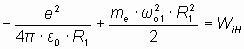 . . | (4) |
Подставляя в уравнение (4) значение ω о2 из уравнения (3), находим:
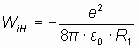 . . | (5) |
Из уравнения (5) можно найти радиус стационарной (первой) орбиты электрона в атоме водорода:
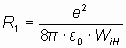 . . | (6) |
Подставляя численное значение энергии ионизации атома водорода (WiH≈-13.595 эВ [1]) получаем ориентировочную величину радиуса первой орбиты электрона:
R1≈0.529598·10-10 [м].
Полученная величина радиуса первой орбиты электрона близка к боровскому радиусу атома водорода, a0=0.52917706·10-10 м [2], но в четвертом знаке все же отличается от него.
При найденном радиусе первой орбиты величина орбитального момента импульса электрона в первом основном энергетическом состоянии атома водорода, в соответствии с определением момента импульса, будет равна:
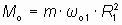 ≈1.055·10-34 [Дж·с].
≈1.055·10-34 [Дж·с].
Угловая частота вращения электрона на первой (стационарной) орбите атома водорода в первом основном энергетическом состоянии может быть найдена из формулы (3):
ω о1.1 ≈4.12921·10 16 [радиан/c].
Полученные величины радиуса первой орбиты электрона, орбитального момента импульса электрона и угловую частоту вращения электрона на первой орбите атома водорода здесь пока не пронумерованы, так как все эти значения далее будут уточнены.
3. Собственные моменты импульса электрона и ядра (протона) в атоме водорода
Рассмотрим возможные величины моментов импульса электрона и протона в атоме водорода. Энергия первого основного энергетического состояния, в качестве которой была взята энергия ионизации, – известна (W1 и W3 в Таблице 1). Ориентировочная величина орбитального момента импульса электрона на первой орбите в первом основном энергетическом состоянии атома водорода также найдена. Наиболее простые соотношения моментов импульса в первом основном энергетическом состоянии представлены в Таблице 1 для энергий W1 и W3. Полагая, что момент импульса ядра при электронных переходах остается неизменным, можно найти момент импульса ядра и сумму моментов импульса электрона, которые совпадают в состояниях W1, W2 и в состояниях W3, W4, соответственно. Определив из данных спектроскопии возможную величину энергии ионизации водорода, когда электрон находится во втором основном энергетическом состоянии (W2≈-16.6+10.2=-3.4 [эВ]), она же – энергия второго энергетического состояния, W2 или W4, можно найти все моменты импульса, представленные в Таблице 1.
Таблица 1.Вероятные моменты импульса электрона и ядра в различных предполагаемых энергетических состояниях на первой орбите атома водорода (в скобках указаны значения в единицах орбитального момента импульса первого энергетического состояния)
| Основное энергетическое состояние | Mo | Ms | Mp | M=Mo+Ms |
| W1 2.17898·10-18 Дж (13.6 эВ) | 1.055·10-34 Дж·с (1) | 0.5275·10-34 Дж·с (1/2) | -1.5825·10-34 Дж·с (-3/2) | 1.5825·10-34 Дж·с (3/2) |
| W2 0.544745·10-18 Дж (3.4 эВ) | 1.84625·10-34 Дж·с (7/4) | -0.26375·10-34 Дж·с (-1/4) | -1.5825·10-34 Дж·с (-3/2) | 1.5825·10-34 Дж·с (3/2) |
При этом необходимо сделать некий разумный выбор в соотношении орбитального и собственного моментов импульса электрона. В Таблице 1. показаны два простейших варианта: первый, − когда собственный момент импульса электрона равен половине орбитального (W1, W2), и второй, − когда собственный момент импульса электрона равен орбитальному моменту импульса (W3, W4). Поскольку любая энергетическая система стремится занять состояние с наименьшей энергией, то в качестве наиболее вероятных основных энергетических состояний атома водорода приняты состояния W1 и W2, как состояния с наименьшей суммой моментов электрона. В соответствии с законом сохранения импульса, определим остальные моменты импульса электрона и протона и поместим их в Таблицу 1. Так как угловая скорость собственного вращения электрона пока не известна, а значение собственного момента импульса электрона было выбрано исходя из простых соотношений, кратных половине орбитального момента импульса, то необходимо оценить допустимость сделанного выбора. Ведь не очевидно, что закон сохранения момента импульса не будет выполняться при других, более сложных соотношениях моментов импульса электрона в атоме.
Собственный момент импульса электрона может быть найден по формуле для гиромагнитного отношения электрона через его собственный магнитный момент, ориентировочную величину которого можно взять из экспериментов по электронному магнитному резонансу (μ e ≈928.47701∙10 -26 Дж/Тл [2, 3]):
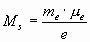 ≈0.527902∙10-34Дж∙с.
≈0.527902∙10-34Дж∙с.
Эта величина собственного магнитного момента электрона очень близка к выбранному в Таблице 1 значению, что говорит о разумности сделанного предварительного выбора. В пользу такого простого (кратного) соотношения моментов говорит и отношение энергий первого и второго энергетических состояний.
Теперь, когда известна величина орбитального момента импульса и ориентировочная величина собственного момента импульса электрона, можно найти величину угловой скорости вращения электрона вокруг собственной оси в первом основном энергетическом состоянии, а также оценить параметры протона: его угловую скорость вращения вокруг собственной оси, его радиус и его магнитный момент. Полученную таким образом величину собственного магнитного момента протона в атоме водорода можно сравнить с имеющимися экспериментальными данными, полученными в экспериментах по магнитному резонансу на ядрах водорода (протонах).
Составим уравнение моментов импульса для атома водорода на его первой орбите:
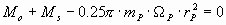 ,
,
Где mp − масса протона, Ω p − угловая скорость протона и rp − радиус протона.
В этом уравнении остаются пока неизвестными две величины: угловая скорость вращения протона вокруг собственной оси и радиус протона.
Радиус ядра атома водорода (протона) можно оценить из следующих соображений. Плотность вещества в электроне известна. Протон также как и электрон является стабильной элементарной частицей вещества и также должен иметь максимально возможную плотность, так как вследствие своей элементарности и неделимости по всей вероятности внутри себя не имеет промежутков объема, свободных от вещества. Поэтому можно предположить, что радиус протона равен:
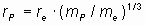 .
.
Так как величина момента импульса протона в первом основном энергетическом состоянии атома водорода равна сумме орбитального и собственного моментов импульса электрона, Mp≈1.58251·10-34Дж·с, масса протона mp=1.6736485·10-27 кг [2], масса электрона me=9.109534·10-31 кг [2], а радиус электрона re=2.817938·10-15 м, то:
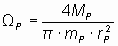 ≈1.01173·1020 [радиан/с].
≈1.01173·1020 [радиан/с].
Теперь можно найти магнитный момент протона в атоме водорода [4]:
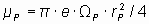 ≈1.51588·10-26 Дж/Тл.
≈1.51588·10-26 Дж/Тл.
Полученная величина магнитного момента протона не намного отличается от известного значения магнитного момента протона [3] (на ~7% больше).
Возможное различие можно попытаться объяснить незнанием точной формы протона и точной величины его радиуса и плотности, недостаточно точными величинами моментов электрона, но, как показано в [4], − это результат взаимодействия магнитного поля электрона с магнитным полем протона.
Таким образом, выбранное в Таблице 1 соотношение величин моментов импульса электрона и ядра в атоме водорода для энергетических состояний W1 и W2 не противоречит экспериментальным результатам, полученным независимым способом.
