Абсолютно черное тело. Закон Кирхгофа.
Абсолютно черное тело. Закон Кирхгофа.
Тепловое излучение
Любое нагретое тело излучает электромагнитные волны. Излучение сильно нагретых тел обнаруживается непосредственно органами чувств человека (излучение Солнца, лампы накаливания, костра, нагретого металла). Излучение менее нагретых тел, хотя и не видно, тем не менее существует и обнаруживается приборами (например, микроволновыми датчиками автомобильных охранных систем или автоматически открывающихся дверей, реагирующими на излучение тела приближающегося человека). Тепловое излучение тел не следует путать с отраженным или рассеянным телами излучением, которое упало на эти тела от других источников излучения.
Основные характеристики теплового излучения:
1) световой потокº мощность излучения – это величина энергии, излучаемая веществом в единицу времени:
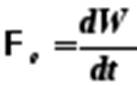 , (5-3)
, (5-3)
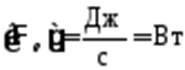 .
.
2) энергетическая светимость излучения – это величина энергии, излучаемая веществом в единицу времени с поверхности единичной площади:
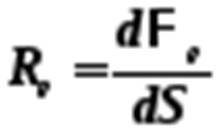 , (5-4)
, (5-4)
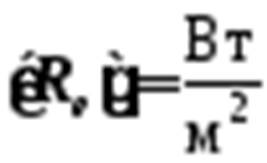 .
.
3) излучательная способность веществаº спектральная плотность энергетической светимости – это величина энергии, излучаемая веществом в единицу времени с поверхности единичной площади в единичном интервале частот или в единичном интервале длин волн:
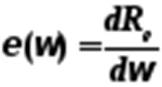 ,
, 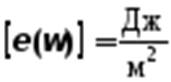 , (5-5а)
, (5-5а)
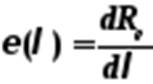 ,
, 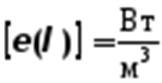 . (5-5б)
. (5-5б)
Связь междуe(w) иe(l) - ?
Т. к. энергетическая светимость вещества одинаковая при даннойТ, то можно записать
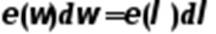

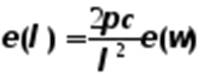 . (5-6)
. (5-6)
Основная задача при объяснении механизма теплового излучения – найти выражение дляe(w) илиe(l).
При облучении электромагнитным излучением любого вещества часть светового потока отражается 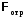 , часть поглощается веществом
, часть поглощается веществом 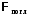 и остаток проходит сквозь вещество
и остаток проходит сквозь вещество 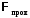 .
.

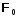 =
= 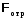 +
+ 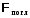 +
+ 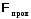
где 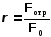 - отражательная способность вещества (коэффициент отражения);
- отражательная способность вещества (коэффициент отражения);
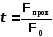 - коэффициент прозрачности вещества;
- коэффициент прозрачности вещества;
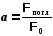 -поглощательная способность вещества (коэффициент поглощения).
-поглощательная способность вещества (коэффициент поглощения).
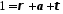
Свойства теплового излучения (интенсивность, диапазон длин волн, распределение интенсивности излучения по длинам волн) определяются характеристиками поверхности тела и его температурой.
Наиболее простой моделью нагретых тел является модель абсолютно черного тела (АЧТ). Вещество, у которого 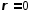 и
и  (ничего не отражает и ничего не пропускает, а все поглощаета = 1), называется абсолютно черным телом (АЧТ).
(ничего не отражает и ничего не пропускает, а все поглощаета = 1), называется абсолютно черным телом (АЧТ).
Свойства излучения АЧТ определяются только его температурой.
 Модель АЧТ:
Модель АЧТ:
Экспериментально была исследована зависимость излучательной способности АЧТ от частоты излучения, которая имеет вид:
 Все попытки классической физики объяснить механизм теплового излучения с позиции электромагнитной теории не привели к успеху.
Все попытки классической физики объяснить механизм теплового излучения с позиции электромагнитной теории не привели к успеху.
Изучение нечерных тел
Нечерными телами в противоположность черным называют тела с поглощательной способностью 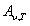 , меньшей единицы. К этой категории принадлежат практически все тела, начиная от сажи, коэффициент поглощения которой близок к 0,99, и кончая хорошо полированными металлами, для которых коэффициент поглощения не превосходит нескольких процентов.
, меньшей единицы. К этой категории принадлежат практически все тела, начиная от сажи, коэффициент поглощения которой близок к 0,99, и кончая хорошо полированными металлами, для которых коэффициент поглощения не превосходит нескольких процентов.
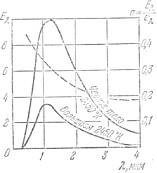
Рис. 1.7. Испускательная способность чёрного тела и вольфрама при температуре 2450 К.
Пунктирная кривая, дающая отношение 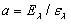 , показывает, что относительное излучение вольфрама растет по мере уменьшения длины волны (селективность излучения вольфрама).
, показывает, что относительное излучение вольфрама растет по мере уменьшения длины волны (селективность излучения вольфрама).
Согласно основному соотношению Кирхгофа 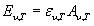 .Следовательно, для нечерных тел
.Следовательно, для нечерных тел 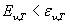 , ибо
, ибо 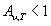 . Это значит, что для любой длины волны испускательная способность нечерного тела не может быть больше испускательной способности черного тела при одинаковой температуре. Сам вид функции
. Это значит, что для любой длины волны испускательная способность нечерного тела не может быть больше испускательной способности черного тела при одинаковой температуре. Сам вид функции 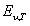 может отличаться от функции
может отличаться от функции 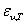 - вследствие того, что поглощательная способность
- вследствие того, что поглощательная способность 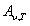 зависит от
зависит от 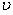 , т. е. обладает избирательным (селективным) ходом.
, т. е. обладает избирательным (селективным) ходом.
В соответствии с этим и излучение нечерного тела может иметь селективный характер.
Примером такого практически важного селективно излучающего вещества является вольфрам. Рис. 1.7 показывает зависимость испускательной способности вольфрама 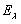 при Т=2450К от длины волны. Для сравнения там же приведена кривая зависимости
при Т=2450К от длины волны. Для сравнения там же приведена кривая зависимости 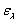 от
от 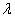 при той же температуре для черного тела. Пунктирная кривая показывает отношение ординат обеих кривых
при той же температуре для черного тела. Пунктирная кривая показывает отношение ординат обеих кривых 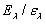 . Из хода пунктирной кривой видно, во-первых, что испускание вольфрама для всех длин воли меньше, чем испускание черного тела (
. Из хода пунктирной кривой видно, во-первых, что испускание вольфрама для всех длин воли меньше, чем испускание черного тела ( 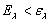 ) и, во-вторых, что вольфрам обладает заметным селективным излучением в видимой части спектра (отношение
) и, во-вторых, что вольфрам обладает заметным селективным излучением в видимой части спектра (отношение 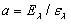 быстро растет с уменьшением
быстро растет с уменьшением 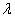 ). Последнее обстоятельство делает вольфрам выгодным материалом для осветительных ламп накаливания.
). Последнее обстоятельство делает вольфрам выгодным материалом для осветительных ламп накаливания.
Напомним еще раз, что закон Кирхгофа относится только к температурному излучению, и в случае, когда свечение обусловлено другими причинами, он не имеет силы. Так, например, при фото- или хемилюминесценции интенсивность свечения в целом ряде спектральных областей гораздо выше, чем у температурного излучения черного тела при температуре люминесцирующего тела. Закон Кирхгофа настолько характерен для температурного излучения, что может служить самым надежным критерием для распознавания природы свечения: свечение, не подчиняющееся закону Кирхгофа, заведомо не является температурным.
Вопрос 24. Формула Рэлея – Джинса. Формула Планка.
Венцом классической физики в объяснении механизма теплового излучения стала формула, полученная Релеем и Джинсом, для излучательной способности АЧТ:
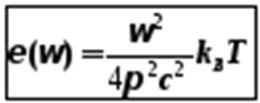 , (5-11)
, (5-11)
- формула Релея-Джинса для теплового излучения.
Эта формула очень хорошо совпадала с экспериментом в области коротких частот (больших длин волн).
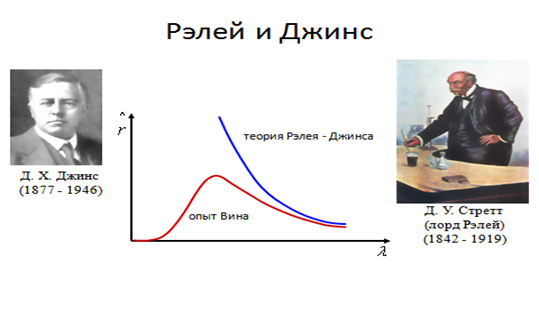
 Однако в области больших частот (коротких длин волн) формула Релея-Джинса терпит катастрофу ®«ультрафиолетовая катастрофа».
Однако в области больших частот (коротких длин волн) формула Релея-Джинса терпит катастрофу ®«ультрафиолетовая катастрофа».
Более того, попытка вычислить RАЧТ тоже приводит к абсурду
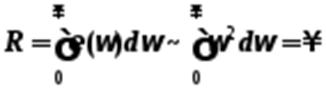 ?
?
Лишь после того, как Макс Планк сформулировал знаменитую гипотезу (носящую его имя) о дискретном характере излучения энергии нагретыми телами, им была получена формула (формула Планка), идеально соответствующая экспериментальному графику универсальной функции Кирхгофа:
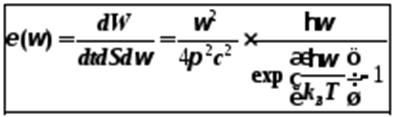 (5-12)
(5-12)
Итоги лекции N 1
1. Немецкий физик Макс Планк в 1900 г. выдвинул гипотезу, согласно которой электромагнитная энергия излучается порциями, квантами энергии. Величина кванта энергии (см. (1.2):
ε = hv,
где h=6,6261·10-34Дж·с - постоянная Планка, v - частота колебаний электромагнитной волны, излучаемой телом.
Эта гипотеза позволила Планку решить проблему излучения абсолютно черного тела.
2. А Эйнштейн, развивая понятие Планка о квантах энергии ввел в 1905 г. понятие "квант света" или фотон. Согласно Эйнштейну квант электромагнитной энергии ε = hv движется в виде фотона, локализованного в малой области пространства. Представление о фотонах позволило Эйнштейну решить проблему фотоэффекта.
3. Английский физик Э. Резерфорд, основываясь на экспериментальных исследованиях, проведенных в 1909-1910 гг., построил планетарную модель атома. Согласно этой модели в центре атома расположено очень маленькое ядро (rя ~ 10-15 м), в котором сосредоточена почти вся масса атома. Заряд ядра положителен. Отрицательно заряженные электроны движутся вокруг ядра наподобие планет солнечной системы по орбитам, размер которых ~ 10-10 м.
4. Атом в модели Резерфорда оказался неустойчивым: согласно электродинамике Максвелла электроны, двигаясь по круговым орбитам, должны непрерывно излучать энергию, в результате чего за время ~ 10-8 с они должны упасть на ядро. Но весь наш опыт свидетельствует о стабильности атома. Так возникла проблема стабильности атома.
5. Решил проблему стабильности атома в 1913 г. датский физик Нильс Бор на основе выдвинутых им двух постулатов. В теории атома водорода, развитой Н. Бором, существенную роль играет постоянная Планка.
6. Тепловым называется электромагнитное излучение, испускаемое веществом за счет его внутренней энергии. Тепловое излучение может находиться в термодинамическом равновесии с окружающими телами.
7. Энергетическая светимость тела R - это отношение энергии dE, испускаемой за время dt поверхностью dS по всем направлениям, к dt и dS (см. (1.5)):

8. Спектральная плотность энергетической светимости rλ (или испускательная способность тела) - это отношение энергетической светимости dR, взятой в бесконечно малом интервале длин волн dλ, к величине dλ (см. (1.6)):

9. Поток излучения Ф - это отношение энергии dЕ, переносимой электромагнитным излучением через какую-либо поверхность ко времени переноса dt, значительно превышающему период электромагнитных колебаний (см. (1.13)):

10. Поглощательная способность тела aλ - это отношение поглощаемого телом потока излучения dФλ' в интервале длин волн dλ к падающему на него потоку dФλ в том же интервале dλ, (см. (1.14):

11. Абсолютно черное тело - это тело, для которого поглощательная способность тождественно равна единице для всех длин волн и для любой температуры, т.е.

Абсолютно черное тело - это модельное понятие.
12. Закон Кирхгофа утверждает, что отношение испускательной способности тела rλ к его поглощательной способности аλ одинаково для всех тели является универсальной функцией длины волны λ (или частоты ω) и температуры Т (см. (1.17)):

ЛЕКЦИЯ N 2
Проблема излучения абсолютно черного тела. Формула Планка. Закон Стефана-Больцмана, закон Вина
§ 1. Проблема излучения абсолютно черного тела. Формула Планка
Проблема излучения абсолютно черного тела состояла в том, чтобы теоретически получить зависимостьφ(λ,Т) - спектральную плотность энергетической светимости абсолютно черного тела.
Казалось, что ситуация ясна: при заданной температуре Т молекулы вещества излучающей полости имеют максвелловское распределение по скоростям и излучают электромагнитные волны в соответствии с законами классической электродинамики. Излучение находится в термодинамическом равновесии с веществом, значит для нахождения спектральной плотности энергии излучения u(λ,T) и связанной с ней функции φ(λ,Т) можно использовать законы термодинамики и классической статистики.
Однако, все попытки теоретиков получить на основе классической физики закон излучения абсолютно черного тела потерпели неудачу.
Частичный вклад в решение этой проблемы внесли Густав Кирхгоф, Вильгельм Вин, Иозеф Стефан, Людвиг Больцман, Джон Уильям Релей, Джеймс Хонвуд Джинс.
Проблема излучения абсолютно черного тела была решена Максом Планком. Для этого ему пришлось отказаться от классических представлений и сделать предположение о том, что заряд, совершающий колебания с частотой v, может получать или отдавать энергию порциями, или квантами.
Величина кванта энергии в соответствии с (1.2) и (1.4):

где h - постоянная Планка;  v - частота колебаний электромагнитной волны, излученной колеблющемся зарядом; ω = 2πv - круговая частота.
v - частота колебаний электромагнитной волны, излученной колеблющемся зарядом; ω = 2πv - круговая частота.
На основе представления о квантах энергии М. Планк, используя методы статистической термодинамики, получил выражение для функции u(ω,Т), дающей распределение плотности энергии в спектре излучения абсолютного черного тела:

Вывод этой формулы будет дан в лекции N 12, § 3 после того, как мы познакомимся с основами квантовой статистики.
Для перехода к спектральной плотности энергетической светимости f(ω,Т) запишем вторую формулу (1.19):

Используя это соотношение и формулу Планка (2.1) для u(ω,T), получим, что:

Это и есть формула Планка для спектральной плотности энергетической светимости f(ω,T).
Теперь мы получим формулу Планка для φ(λ,Т).Как мы знаем из (1.18), в случае абсолютно черного тела f(ω,T) = rω, а φ(λ,Т) = rλ.
Связь между rλ и rω дает формула (1.12), применяя ее мы получим:

Здесь мы аргумент ω функции f(ω,Т) выразили через длину волны λ. Подставляя сюда формулу Планка для f(ω,Т)из (2.2), получим формулу Планка для φ(λ,Т) - спектральной плотности энергетической светимости в зависимости от длины волны λ:

График этой функции хорошо совпадает с экспериментальными графиками φ(λ,Т) для всех длин волн и температур.
Это и означает, что проблем излучения абсолютно черного тела решена.
§ 2. Закон Стефана-Больцманаи закон Вина
Из (1.11) для абсолютно черного тела, когда rω = f(λ,Т), получим энергетическую светимость R(T), интегрируя функцию f(ω,Т) (2.2) во всем интервале частот.

Интегрирование дает:

Введем обозначение:

тогда выражение для энергетической светимости R примет следующий вид:

Это и есть закон Стефана-Больцмана.
М. Стефан на основе анализа опытных данных пришел в 1879 г. к выводу, что энергетическая светимость любого тела пропорциональна четвертой степени температуры.
Л. Больцман в 1884 г. нашел из термодинамических соображений, что такая зависимость энергетической светимости от температуры справедлива лишь для абсолютно черного тела.
Постоянная σ носит название постоянной Стефана-Больцмана. Ее экспериментальное значение:

Вычисления по теоретической формуле дают для σ результат очень хорошо согласующийся с экспериментальным.
Отметим, что графически энергетическая светимость равна площади, ограниченной графиком функции f(ω,Т), это иллюстрирует рисунок 2.1.

Рис. 2.1
Максимум графика спектральной плотности энергетической светимости φ(λ,Т) при повышении температуры смещается в область более коротких волн (рис. 2.2). Для нахождения закона, по которому происходит смещение максимума φ(λ,Т) в зависимости от температуры, надо исследовать функцию φ(λ,Т) на максимум. Определив положение этого максимума, мы получим закон его перемещения с изменением температуры.

Рис. 2.2
Как известно из математики, для исследования функции на максимум надо найти ее производную и приравнять к нулю:

Подставив сюда φ(λ,Т) из (1.23) и взяв производную, получим три корня алгебраического уравнения относительно переменной λ. Два из них (λ = 0 и λ = ∞) соответствуют нулевым минимумам функции φ(λ,Т). Для третьего корня получается приближенное выражение:

Введем обозначение:

тогда положение максимума функции φ(λ,Т) будет определятся простой формулой:

Это и есть закон смещения Вина.
Он назван так в честь В. Вина, теоретически получившим в 1894 г. это соотношение. Постоянная в законе смещения Вина имеет следующее численное значение:

Итоги лекции N 2
1. Проблема излучения абсолютно черного тела состояла в том, что все попытки получить на основе классической физики зависимость φ(λ,Т) - спектральную плотность энергетической светимости абсолютно черного тела потерпели неудачу.
2. Эту проблему решил в 1900 г. М. Планк на основе своей гипотезы квантов: заряд, совершающий колебания с частотой v, может получить или отдавать энергию порциями или квантами. Величина кванта энергии:

здесь h = 6,626 ·10-34 - постоянная Планка, величина  Дж·с также называется постоянной Планка ["аш" с чертой], ω - круговая (циклическая) частота.
Дж·с также называется постоянной Планка ["аш" с чертой], ω - круговая (циклическая) частота.
3. Формула Планка для спектральной плотности энергетической светимости абсолютно черного тела имеет следующий вид (см. (2.4):

здесь λ - длина волны электромагнитного излучения, Т - абсолютная температура, h - постоянная Планка, с - скорость света в вакууме, k - постоянная Больцмана.
4. Из формулы Планка следует выражение для энергетической светимости R абсолютно черного тела:

которое позволяет теоретически вычислить постоянную Стефана-Больцмана (см. (2.5)):

теоретическое значение которой хорошо совпадает с ее экспериментальным значением:

в законе Стефана-Больцмана (см.(2.6)):

5. Из формулы Планка следует закон смещения Вина, определяющий λmax - положение максимума функции φ(λ,Т) в зависимости от абсолютной температуры (см. (2.9):

Для b - постоянной Вина - из формулы Планка получается следующее выражение (см. (2.8)):

Постоянная Вина имеет следующее значение b = 2,90 ·10-3 м·К.
ЛЕКЦИЯ N 3
Проблема фотоэффекта. Уравнение Эйнштейна для фотоэффекта
§ 1. Проблема фотоэффекта
Фотоэффект - это испускание электронов веществом под действием электромагнитного излучения.
Такой фотоэффект называют внешним. Именно о нем мы будем говорить в этой главе. Есть еще и внутренний фотоэффект. (см. лекцию 13, § 2).
В 1887 г. немецкий физик Генрих Герц обнаружил, что ультрафиолетовый свет, освещающий отрицательный электрод в разряднике, облегчает прохождение разряда. В 1888-89 гг. русский физик А. Г. Столетов занимается систематическим исследованием фотоэффекта (схема его установки приведена на рисунке). Исследования проводились в атмосфере газа, что сильно усложняло происходившие процессы.

Рис. 3.1
Столетов обнаружил, что:
1) наибольшее воздействие оказывают ультрафиолетовые лучи;
2) сила тока возрастает с увеличением интенсивности света, освещающего фотокатод;
3) испущенные под действием света заряды имеют отрицательный знак.
Дальнейшие исследования фотоэффекта производились в 1900-1904 гг. немецким физиком Ф. Ленардом в наивысшем достигнутом в то время вакууме.
Ленарду удалось установить, что скорость вылетающих из фотокатода электронов не зависит от интенсивности света и прямо пропорционально его частоте. Так родилась проблема фотоэффекта. Объяснить результаты опытов Ленарда на основе электродинамики Максвелла было невозможно!
На рисунке 3.2 изображена установка, позволяющая детально изучать фотоэффект.

Рис. 3.2
Электроды, фотокатод и анод, помещены в баллон, из которого откачан воздух. Свет на фотокатод подается через кварцевое окошко. Кварц, в отличие от стекла, хорошо пропускает ультрафиолетовые лучи. Разность потенциалов (напряжение) между фотокатодом и анодом измеряет вольтметр. Ток в цепи анода измеряется чувствительным микроамперметром. Для регулировки напряжения батарея питанияподключена к реостату со средней точкой. Если движок реостата стоит против средней точки, подсоединенной через микроамперметр к аноду, то разность потенциалов между фотокатодом и анодом равна нулю. При смещении движка влево, потенциал анода становится отрицательным относительно катода. Если движок реостата сдвигать вправо от средней точки, то потенциал анода становится положительным.
Вольт-амперная характеристика установки по изучению фотоэффекта позволяет получить информацию об энергии электронов, испускаемых фотокатодом.
Вольт-амперная характеристика - это зависимость фототока i от напряжения между катодом и анодом U. При освещении светом, частота v которого достаточна для возникновения фотоэффекта, вольт-амперная характеристика имеет вид графика, изображенного на рис. 3.3:

Рис. 3.3
Из этой характеристики следует, что при некотором положительном напряжении на аноде фототок i достигает насыщения. При этом все электроны, испущенные фотокатодом в единицу времени, попадают за это же время на анод.
При U = 0 часть электронов долетает до анода и создает фототок i0. При некотором отрицательном напряжении на аноде - Uзад - фототок прекращается. При этом значении напряжения максимальная кинетическая энергия фотоэлектрона у фотокатода (mv2max)/2 полностью расходуется на совершение работы против сил электрического поля:

В этой формуле me - масса электрона; vmax - его максимальная скорость у фотокатода; e - абсолютное значение заряда электрона.
Таким образом, измерив задерживающее напряжение Uзад, можно найти кинетическую энергию (и скорость электрона) сразу после его вылета из фотокатода.
Опыт показал, что
1)энергия вылетевших из фотокатода электронов (и их скорость) не зависела от интенсивности света!При изменении частоты света v меняется и Uзад, т.е. максимальная кинетическая энергия электронов, покидающих фотокатод;
2)максимальная кинетическая энергия электронов, у фотокатода, (mv2max)/2, прямо пропорциональна частоте v света, освещающего фотокатод.
Проблема, как и в случае с излучением абсолютно черного тела, состояла в том, что теоретические предсказания, сделанные для фотоэффекта на основе классической физики (электродинамики Максвелла), противоречили результатам опытов. Интенсивность света I в классической электродинамике является плотностью потока энергии световой волны. Во-первых, с этой точки зрения, энергия, передаваемая световой волной электрону, должна быть пропорциональна интенсивности света. Опыт не подтверждает это предсказание.Во-вторых, в классической электродинамике нет никаких объяснений прямой пропорциональности кинетической энергии электронов, (mv2max)/2, частоте света v.
Вопрос №1
Какое излучение называется тепловым? Что называется интегральной лучеиспускательной способностью тела ( энергетической светимостью), монохроматической лучеиспускательной способностью тела ( оптической плотностью энергетической светимости), поглощательной способностью тела?
Тепловое излучение – излучение, которое происходит за счет внутренней энергии тел.
Все другие виды свечения возбуждаемее за счёт энергии нетеплового происхождения называетсялюминесценцией:
- Хемилюминесценция (Свечение фосфора);
- Свечение в газах и твердых телах под действием электрического поля;
- При бомбардировке твердых тел электронами, возникает катодолюминесценция;
- Фотолюминесценция (под действием поглощаемого электромагнитного излучения).
Энергетическая светимость (Rt) – энергия испускаемая с единицы поверхности излучаемого тела по всем направлениям во всем интервале длин волн или частот (зависит от температуры).
Если рассматривать поток энергии в узком интервале dV, то
dRt ~ dV
dRt = rdV – излучательная( испускательная) способность.
Испускательная способность – энергия, излучаемая с единицы поверхности в узком интервале длин волн dV.
а– поглощательная способность. Показывает какая доля энергии, падающей на тело, этим телом поглощается.
а = W(погл)/W(пад)
W(пад)– энергия, падающая на тело;
W(погл)– энергия, поглощаемая телом.
Если а = 1, то это абсолютно черное тело.(Таких тел не бывает);
Еслиа меньше нуля, такие тела – серые.
КВАНТОВАЯ ОПТИКА.
ТЕПЛОВОЕ ИЗЛУЧЕНИЕ.
Раздел оптики занимающийся изучением явлений, в которых проявляются квантовые свойства света
Абсолютно черное тело
Количественной характеристикой теплового излучения служит спектральная плотность энергетической светимости - лучеиспускательная способность (rν,T) - определяет количество энергии, излучаемой с единицы площади поверхности излучающего тела за единицу времени в единичном интервале частот от ν до ν + dν
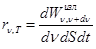 (1)
(1)
[rν,T] = Дж/м2
где rν,T - является функцией частоты и температуры. Используется также запись rλ,T - функция длины волны и температуры. Найдем связь между ними.
Из (1) следует
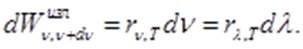
Так как λ = с/ν, следовательно
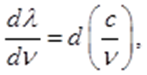
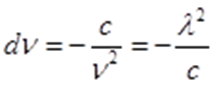
где с - скорость света, равная 3·108 м/с,
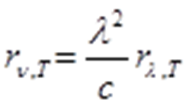
Второй характеристикой теплового излучения является поглощающая способность - аν,Т, которая также является функцией частоты и температуры. Поглощающая способность аν,Т (или коэффициент поглощения) показывает, какая часть энергии падающей за единицу времени на единицу плоской поверхности данного тела, поглощается.
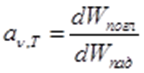
аν,Т ≤ 1, [аν,Т] = l (безразмерная величина).
Тело, коэффициент поглощения которого равен 1, называется абсолютно черным телом (а.ч.т.). Абсолютно черное тело способно поглощать полностью при любой температуре всё падающее на тело излучение любой частоты.
Абсолютно черного тела в природе нет, однако сажа, черный бархат, зрачок глаза в определенном интервале частот по своим свойствам близки к абсолютно черному телу.
Идеальной моделью черного тела является замкнутая полость с небольшим отверстием.
Луч света в полости в результате многократных отражений от стенок полностью
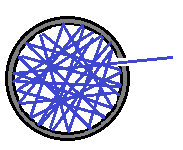 поглощается. Чем меньше величина отверстия, тем меньше интенсивность выходящего света, тем ближе коэффициент поглощения к 1. Примером такой полости может быть зрачок глаза.
поглощается. Чем меньше величина отверстия, тем меньше интенсивность выходящего света, тем ближе коэффициент поглощения к 1. Примером такой полости может быть зрачок глаза.
Тело с полостью - пример абсолютно черного тела (аν,Т =1).
Если аν,Т< 1 и при этом аν,Т = const, то тело является серым.
Закон. Кирхгофа
Кирхгоф в 1855 году установил закон, согласно которому, отношение лучеиспускательной способности данного тела к поглощающей способности есть величина, не зависящая от природы тела, является для всех тел универсальной функцией частоты (длины волны) и температуры, равная лучеиспускательной способности абсолютно черного тела.
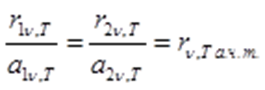
Следствие закона Кирхгофа:
1. Так как для любого тела аν,Т< 1, то из закона Кирхгофа следует, что лучеиспускательная способность любого тела rν,Т<rν,Та.ч.т.
rν,Т = aν,Т ·rν,Та.ч.т.
1. Если, тело не поглощает электромагнитное излучение какай-то частоты ν, то есть aν,Т = 0, то оно его и не излучает, так как rν,Т = aν,Т ·rν,Та.ч.т. = 0.
Закон Кирхгофа описывает только тепловое излучение. Излучение, которое не подчиняется закону Кирхгофа, не является тепловым - критерий теплового излучения.
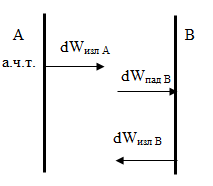 Закон Кирхгофа можно получить, рассматривая равновесное тепловое излучение. Пусть даны две пластины, изолированные от внешней среды. При этом пластика А является а.ч.т. А и В находятся в условиях термодинамического равновесия.
Закон Кирхгофа можно получить, рассматривая равновесное тепловое излучение. Пусть даны две пластины, изолированные от внешней среды. При этом пластика А является а.ч.т. А и В находятся в условиях термодинамического равновесия.
dWпогл = aν,ТdWпад
dWпад = dWизл , так как наблюдается термодинамическое равновесие
dWпад В = dWизл А =rν,Та.ч.т.dν ;
dWпогл B = aν,ТdWпад B = aν,Тrν,Та.ч.т.dν= dWизл B = rν,Тdν
rν,Т = aν,Т ·rν,Та.ч.т., следовательно, rν,Т /aν,Т = rν,Та.ч.т
Ввиду того, что поверхность В выбрана совершенно произвольно, полученный результат будет справедлив в случае любой поверхности.
Самым распространенным в природе видом электромагнитного излучения является тепловое излучение, или лучеиспускание; оно совершается за счет энергии теплового движения атомов и молекул вещества, т. е. за счет внутренней энергии вещества, и потому ведет к охлаждению излучающего тела. Лучеиспускание присуще всем телам при любой температуре, отличной от абсолютного нуля. Тепловое излучение имеет сплошной спектр, однако распределение энергии в нем существенно зависит от температуры: при низких температурах тепловое излучение является преимущественно инфракрасным, при высоких температурах — видимым и ультрафиолетовым.
Всякое тело, излучая само, вместе с тем поглощает часть лучистой энергии, испускаемой другими (окружающими) телами; этот процесс называется лучепоглощением. Он ведет к нагреванию данного тела.
Очевидно, что, теряя энергию путем лучеиспускания и в то же время получая энергию путем лучепоглощения, данное тело должно в конце концов прийти в состояние теплового, или лучистого, равновесия, при котором потеря энергии за счет лучеиспускания компенсируется притоком энергии за счет лучепоглощения. Температура, соответствующая этому состоянию, называется температурой лучистого равновесия.
Воображаемое тело, поглощающее при любой температуре всю падающую на него лучистую энергию, называется абсолютно черным телом\ лучепоглощательная способность такого тела для всех длин волн одинакова и равна единице (Лх = А = 1). Для видимой части спектра телом, близким по своим свойствам к абсолютно черному, является сажа (А = 0,95).
Практически наиболее совершенным абсолютно черным телом является малое отверстие в рИс. 352 стенке замкнутой полости, внутренняя поверхность которой зачернена (рис. 352). Луч, попавший в отверстие, многократно отражается стенками полости и практически не выходит обратно, поскольку при каждом отражении значительная часть его энергии поглощается стенками
Абсолютно черное тело, поглощая падающую на него лучистую энергию, вместе с тем само излучает. Поэтому при низкой температуре полости отверстие в ней кажется черным; если же полость нагрета до высокой температуры, то отверстие представляется ярко светящимся. Примерами практически абсолютно черных тел могут служить зрачок глаза и смотровое отверстие мартеновской печи.
Закон излучения Кирхгофа -Отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты и не зависит от их формы и химической природы. Известно, что при падении электромагнитного излучения на некоторое тело часть его отражается, часть поглощается и часть может пропускаться. Доля поглощаемого излучения на данной частоте называется поглощательной способностью тела 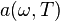 . С другой стороны, каждое нагретое тело излучает энергию по некоторому закону
. С другой стороны, каждое нагретое тело излучает энергию по некоторому закону 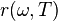 , именуемым излучательной способностью тела.
, именуемым излучательной способностью тела.
Величины 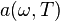 и
и 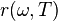 могут сильно меняться при переходе от одного тела к другому, однако согласно закону излучения Кирхгофа отношение испускательной и поглощательной способностей не зависит от природы тела и является универсальной функцией частоты (длины волны) и температуры:
могут сильно меняться при переходе от одного тела к другому, однако согласно закону излучения Кирхгофа отношение испускательной и поглощательной способностей не зависит от природы тела и является универсальной функцией частоты (длины волны) и температуры:
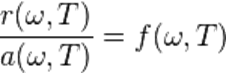
По определению, абсолютно чёрное тело поглощает всё падающее на него излучение, то есть для него 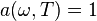 . Поэтому функция
. Поэтому функция 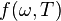 совпадает с излучательной способностью абсолютно чёрного тела, описываемой законом Стефана — Больцмана, вследствие чего излучательная способность любого тела может быть найдена исходя лишь из его поглощательной способности.
совпадает с излучательной способностью абсолютно чёрного тела, описываемой законом Стефана — Больцмана, вследствие чего излучательная способность любого тела может быть найдена исходя лишь из его поглощательной способности.
Законы излучения абсолютно черного тела. Гипотеза Планка
Законы излучения абсолютно чёрного тела[править | править вики-текст]
Классический подход[править | править вики-текст]
Изначально к решению проблемы были применены чисто классические методы, которые дали ряд важных и верных резу
