Интегралы с полиномами лежандра

1.

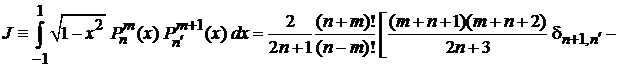
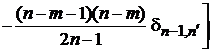. (П.6.12)

Доказательство:

Упрощаем интеграл, используя рекуррентное соотношение

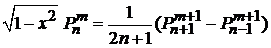, (6.125)

тогда

.

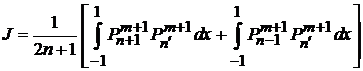Интегралы вычисляем при помощи условия ортонормированности

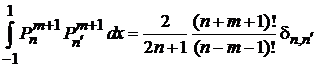. (6.123)

Тогда

,

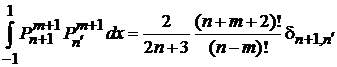где

.

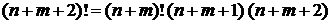Аналогично

,

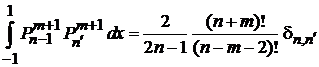где

.

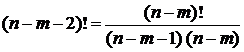В результате получаем (П.6.12).

2. Доказать условия ортогональности

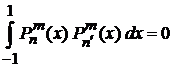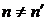, ; (6.123)

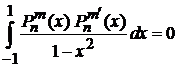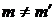, . (6.124)

Доказательство:

Используем уравнение Лежандра (6.115) для 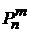и :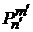

,

.

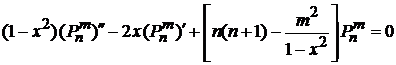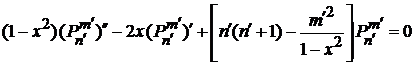Первое уравнение умножаем на 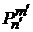, второе – на .

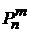Взаимно вычитаем результаты.

Первые два слагаемые дают

.

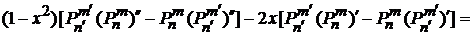
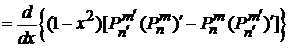Получаем

.

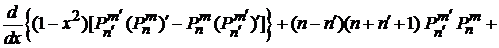
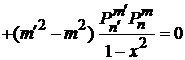Интегрируем по интервалу 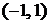. Первое слагаемое дает нуль, тогда

.

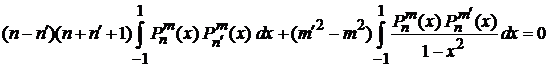При 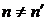, 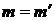получаем (6.123),

при 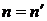, 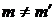получаем (6.124).

3. Доказать условие нормировки полиномов Лежандра

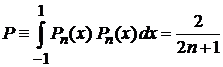. (6.112)

Доказательство:

Подстановка в интеграл

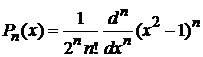(6.96)

дает

.

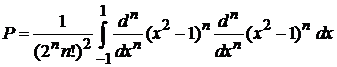Интегрируем по частям n раз, свободные слагаемые дают нули. В результате

,

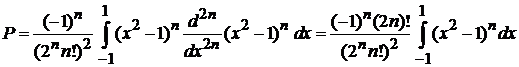где учтено

.

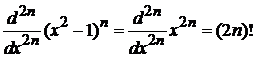Используем

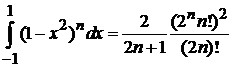, (П.3.9)

и получаем (6.112).

4. Доказать условие нормировки присоединенных функций Лежандра

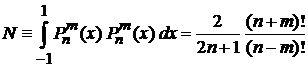. (6.123)

Доказательство:

В интеграл подставляем

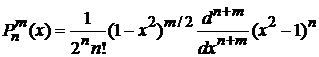, (6.117)

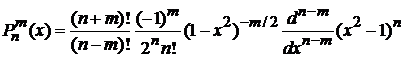, (6.119)

получаем

.

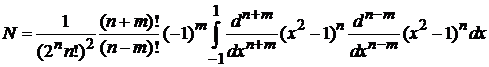Интегрируем по частям 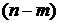раз, полагая

, .

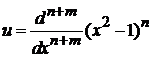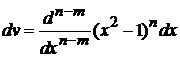Свободные слагаемые дают нули. В результате получаем

.

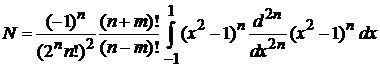Интеграл вычислен в предыдущем примере

,

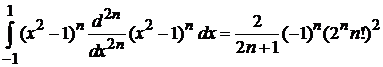в результате

.

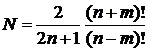Полиномы Чебышева ПЕРВОГО РОДА

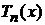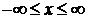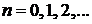, ; – порядок полинома.

Имеют наименьшее отклонение от нуля на интервале 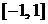и максимальное отклонение за пределами этого интервала по сравнению с другими полиномами того же порядка.

Используются для приближения и интерполирования функций.

Исследовал Пафнутий Львович Чебышев, нем. Tschebyschew, в 1854 г.

Уравнение Чебышева

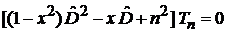. (6.146)

Метод факторизации

1. Уравнение гипергеометрического типа

.

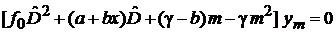Сравнение дает

, , , , ,

, ,

, , ,

, .

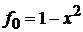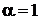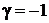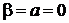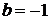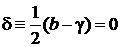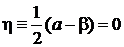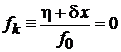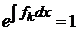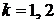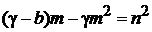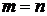2. Весовая функция

,

.

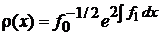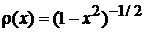3. Решение Родрига

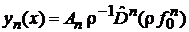дает

.

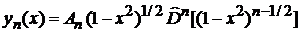Полагаем

,

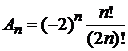полином Чебышева первого рода

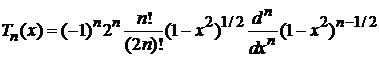. (6.147)

Из (6.147) находим свойство четности и частные значения

,

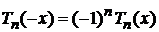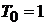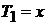, . (6.148)

4. Условие ортонормированности

, .

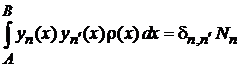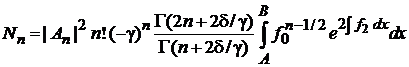Учитываем

,

, ,

,

,

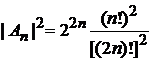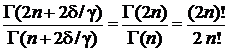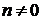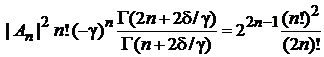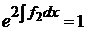находим

.

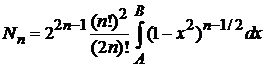Область определения решения не определяется из стандартного условия

.

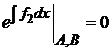Полагаем 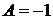, 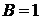и используем

,

.

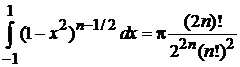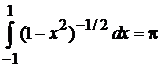В результате получаем

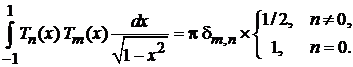(6.149)

Учтено .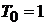

Тригонометрическое представление

В (6.149) заменяем

,

,

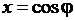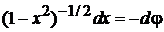получаем

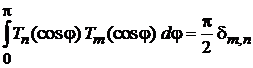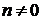, . (6.150)

Учитывая четность 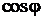, расширяем область интегрирования до 2π:

, .

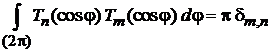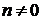Сравниваем с формулой

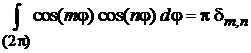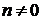, . (1.45)

из темы «Преобразование Фурье периодической функции». Поскольку 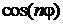– полином степени n по аргументу 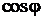, то получаемтригонометрическое представление

,

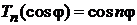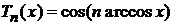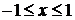, . (6.151)

Воспроизводятся результаты

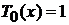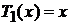, . (6.148)

Расширение области определения

Выражения (6.151) применимы при 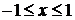, метод факторизации не дает ограничения на область определения.

С учетом

,

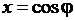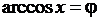
из

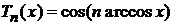(6.151)

по формуле Эйлера

,

,

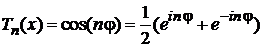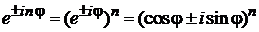получаем

.

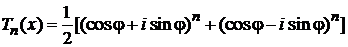Замена

,

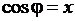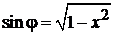
дает

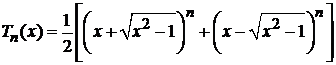. (6.153)

Формула (6.153) применима при .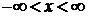

Рекуррентные соотношения

1. Используем

,

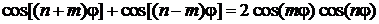полагаем 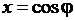, учитываем

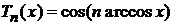, (6.151)

тогда

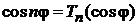. (6.151а)

В результате

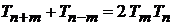. (6.156)

2. В (6.156) при 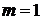используем 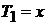, получаем

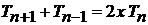. (6.157)

3. В (6.156) при 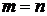используем 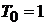, находим

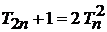. (6.158)

Частные значения

Из

,

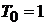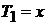
и (6.157) в виде

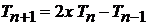
при 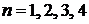находим

, ,

, .

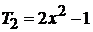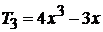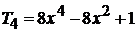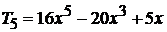Следовательно, 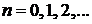– порядок полинома .

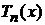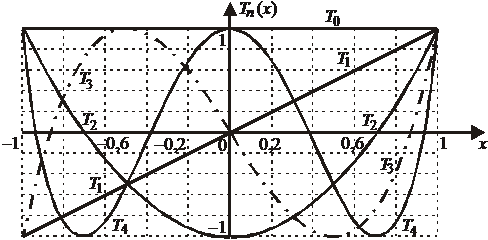
Из тригонометрического представления

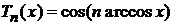, (6.151)

находим

,

,

,

.
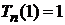
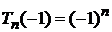
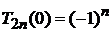
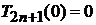