Решение уравнения методом факторизации

1. Уравнение обобщенного гипергеометрического типа

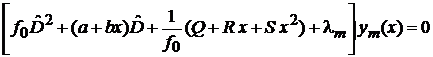, (5.5)

2. , , , ,

,

, ,

, ,

:

;

:

;

;

,

,

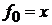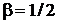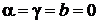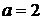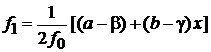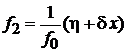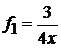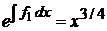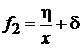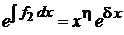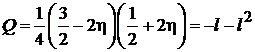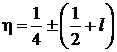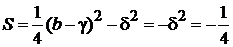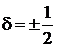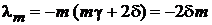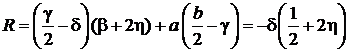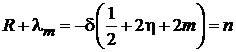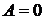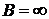3. С учетом и получаем

, , :

,

,

,

,

.

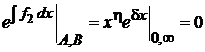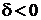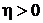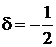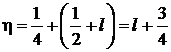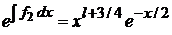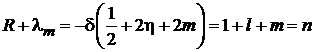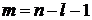4. Из (5.8)

.

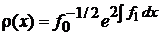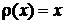5. Если 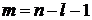– целое не отрицательное число, то применима формула Родрига (5.7)

,

,

,

, .

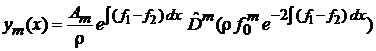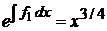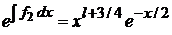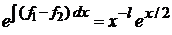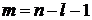дает

,

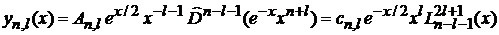где

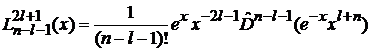
– обобщенный полином Лагерра.

В результате

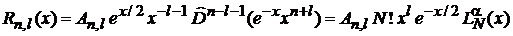, (6.85а)

,

.

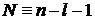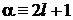Если 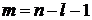– не целое, то нормировка 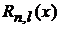не существует и физическое состояние отсутствует.

6. Условие ортонормированности (5.11)

,

,

,

, ,

,

,

, ,

.

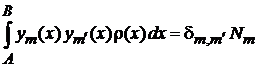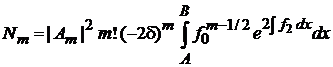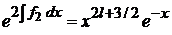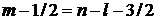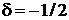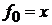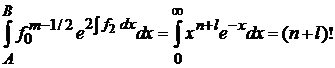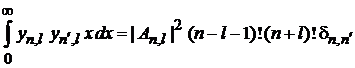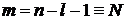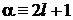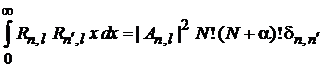Выбираем 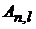из условия ортонормированности в виде

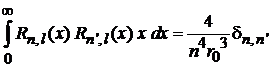. (6.86)

тогда

.

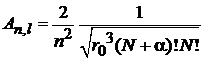Из

(6.85а)

получаем

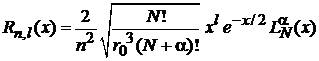, (6.87)

где

, , .

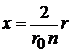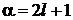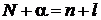Физический смысл параметров

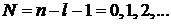
– радиальное квантовое число, равное числу нулей радиальной части волновой функции;

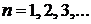
– главное квантовое число определяет энергию электрона

;

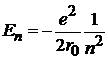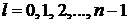
– орбитальное квантовое число определяет модуль момента импульса электрона

;

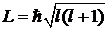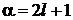
– число проекций на ось z орбитального момента с числом l.

Решения низших порядков:

;

,

.

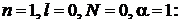
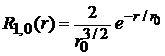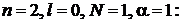
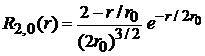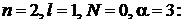
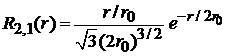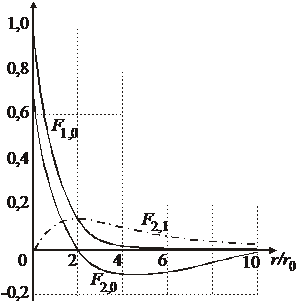
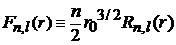
Нормировка плотности вероятности

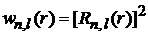
В сферических координатах требуем

, , .

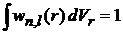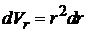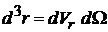Для переменной r

,

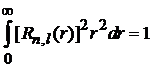для переменной x

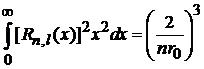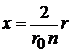, . (6.88)

Нормировка определяет выбор постоянной .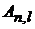

Доказательство (6.88):

Используем

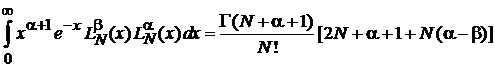(6.76)

при

,

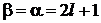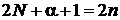
находим

.

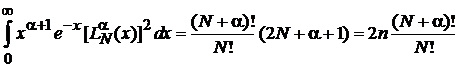Подстановка

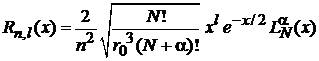(6.87)

дает

,

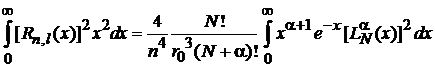и получаем (6.88).

Рекуррентные соотношения

1. Равенство для полиномов Лагерра с одинаковыми порядками α

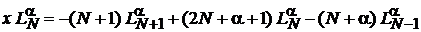(6.58)

умножаем на 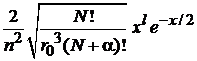и с учетом

, ,

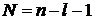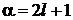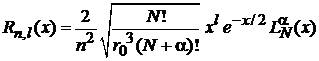(6.87)

получаем соотношение между функциями с одинаковыми l

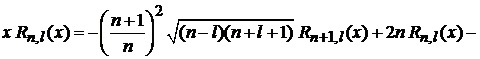
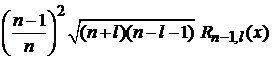– . (6.89)

Дважды используем

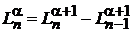, (6.59)

Находим

,

.

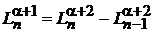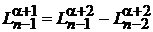В результате

.

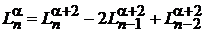Заменяем

, ,

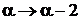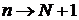Получаем

.

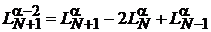Умножаем равенство на

,

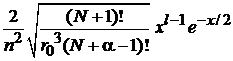И сравниваем с

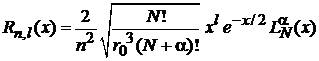, (6.87)

приходим к соотношению, где индекс l у функции, стоящей слева, на единицу меньше, чем у функций, стоящих справа:

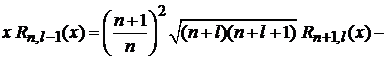
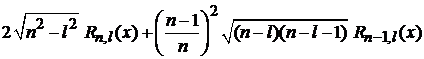– . (6.90)

Используя (6.57) и (6.61), находим

.

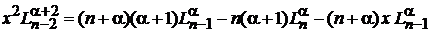Выражая 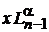с помощью (6.58) и заменяя 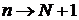, получаем

.

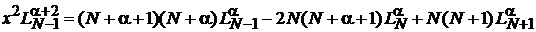Полагая 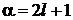, 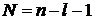и умножая на 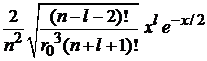, находим соотношение, где индекс l у функции, стоящей слева, на единицу больше, чем у функций, стоящих справа:

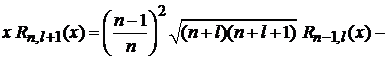
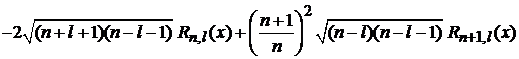. (6.91)

4. Дифференцируем

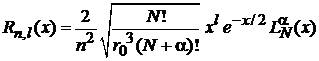, (6.87)

используем

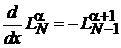, (6.54)

получаем

.

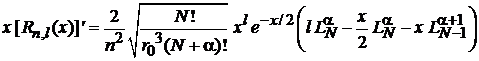Используем рекуррентные соотношения (6.58) и (6.61), которые выравнивают верхний индекс и убирают множитель x из круглой скобки:

.

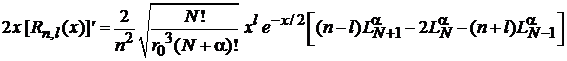В результате

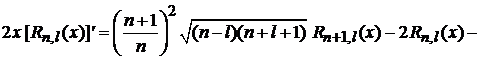
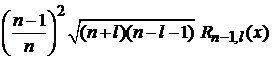– . (6.92)

Вычисление матричных элементов

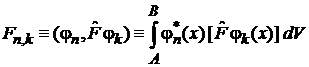, (1)

.

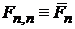1. Среднее расстояние до ядра 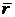электрона в состоянии 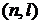в атоме водорода.

С учетом оператора радиуса 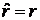и радиального объема 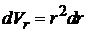, находим

,

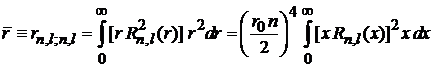где сделана замена 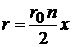. Вычисляем интеграл с помощью условия ортонормированности и рекуррентного соотношения, устраняющего x под интегралом:

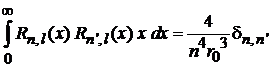(6.86)

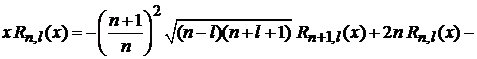
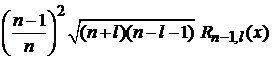– . (6.89)

При возведении в квадрат рекуррентного соотношения условие ортогональности зануляет перекрестные произведения, остается сумма квадратов слагаемых

.

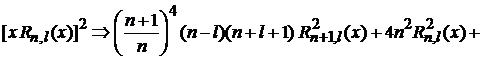
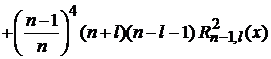С учетом нормировок

,

,

,

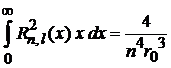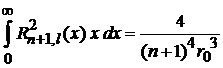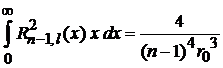находим

.

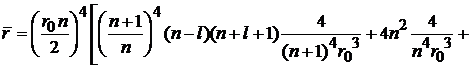
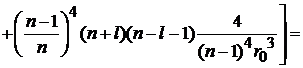
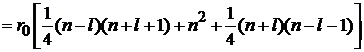В результате

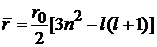. (П.5.8)

2. Рекуррентное соотношение Крамерса

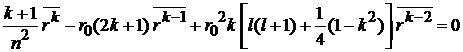, (П.5.10)

где

; .

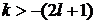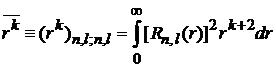Доказательство:

· Интегрируем

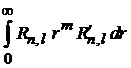
по частям, где

, .

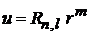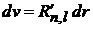Свободное слагаемое обращается в нуль, получаем

.

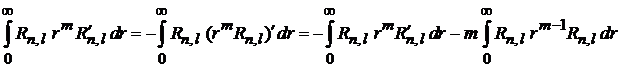В результате

.

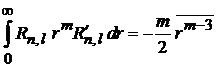· Аналогично находим

,

,

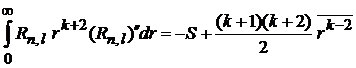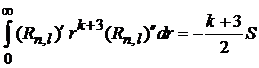где

.

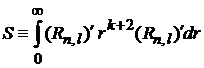· Используем уравнение Шредингера для радиальной функции

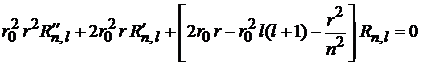. (П.5.11)

Умножая уравнение на 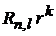, интегрируем и получаем

.

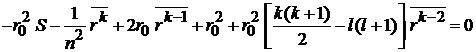Умножаем (П.5.11) на 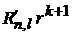, интегрируем и находим

.

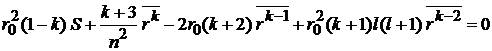· Исключая S из уравнений, получаем (П.5.10).

Частные случаи

1. При 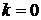из

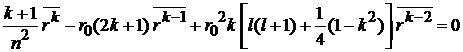, (П.5.10)

находим

,

,

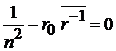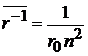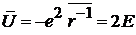
– теорема вириала связывает полную энергию со средним значением потенциальной энергии .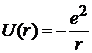

2. При 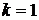получаем

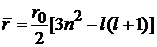. (П.5.8)

3. При 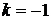находим

.

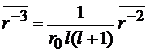Соотношение (П.5.10) не позволяет найти .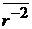

Полиномы Лежандра

, ; ; ;

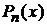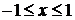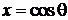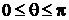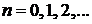
– описывают угловую зависимость в полярных и сферических координатах;

– входят в собственные функции оператора момента импульса и оператора Лапласа;

– множество 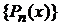образует ортонормированный базис на интервале .

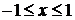Полиномы исследовал Андре Мари Лежандр в 1785 г.

Уравнение Лежандра

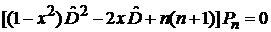, (6.93)

Учитываем

,

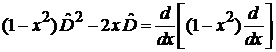тогда

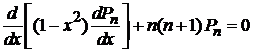. (6.93а)

Для угловой переменной

, ,

,

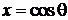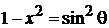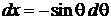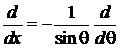
из (6.93а) для 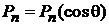получаем

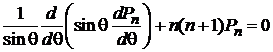. (6.94)

Метод факторизации

1. Уравнение

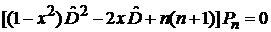(6.93)

гипергеометрического типа

.

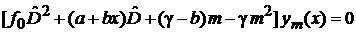2. Сравнение дает

,

, , , ,

, ,

,

,

, ,

,

.

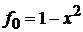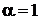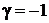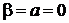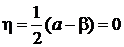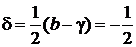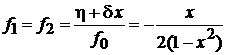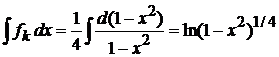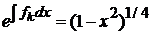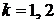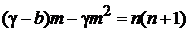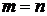3. Граничные условия

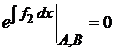в виде

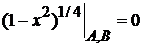
дают

, .

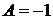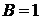4. Весовая функция

,

.

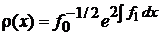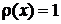5. Решение Родрига

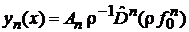дает

.

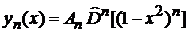Полагаем

,

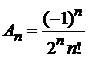получаем формулу Родрига дляполинома Лежандра

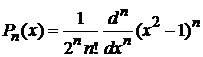. (6.96)

Свойство четности

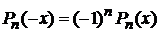, (6.97)

тогда

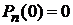, n – нечетное.

6. Ортонормированность

, .

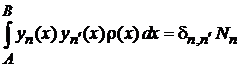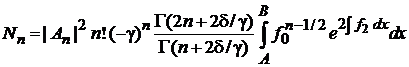Учитываем

, , ,

,

,

,

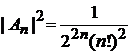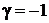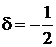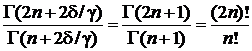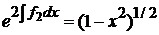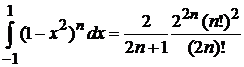тогда условие ортонормированности

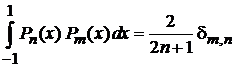. (6.112)

7. Производящая функция

,

,

.

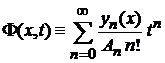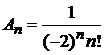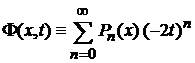Из уравнения для ξ

,

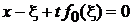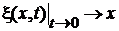в виде

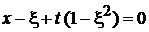
находим решение

,

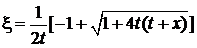которое при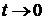

.

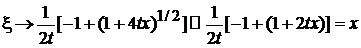Использовано

, .

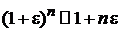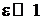Из

,

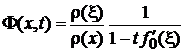с учетом

,

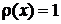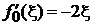
получаем

.

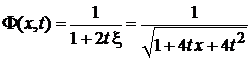Заменяем 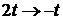, тогда

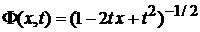, (6.101)

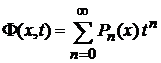. (6.102)