Вычисление физических и механических величин
Предположим, что плоская пластина  имеет поверхностную плотность распределения масс
имеет поверхностную плотность распределения масс 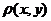 непрерывную в
непрерывную в  . Тогда масса
. Тогда масса 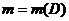 этой пластины вычисляется по формуле
этой пластины вычисляется по формуле
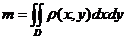 .
.
Моменты инерции 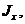
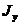 и
и 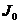 плоской материальной пластины
плоской материальной пластины  с поверхностной плотностью
с поверхностной плотностью 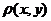 относительно координатных осей
относительно координатных осей 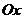 ,
, 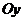 и начала координат
и начала координат 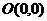 соответственно вычисляются по формулам:
соответственно вычисляются по формулам:
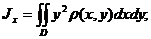
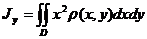 ;
;
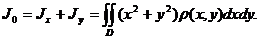
В случае однородной пластины (ρ=1) эти формулы принимают более простой вид:
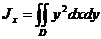 ,
, 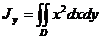 ,
, 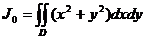 .
.
Координаты центра тяжести материальной пластины  с плотностью
с плотностью 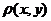 вычисляется по формулам
вычисляется по формулам
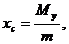
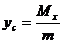 ,
,
где
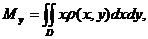
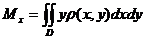 -
-
статические моменты пластины  относительно осей
относительно осей 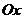 и
и 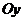 соответственно, а
соответственно, а 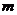 - ее масса.
- ее масса.
В случае однородной пластины соответственно имеем:
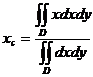 ,
, 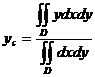 .
.
Пример 1.Вычислить площадь фигуры, ограниченной кривыми 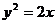 и
и 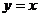 .
.
Имеем 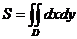 . Порядок интегрирования выберем так, как указано на чертеже (рис. 13)
. Порядок интегрирования выберем так, как указано на чертеже (рис. 13)
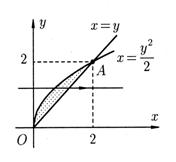
Рис. 13.
Сначала определим координаты точки А:
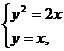
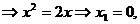
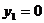 и
и 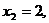
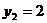 .
.
Проекция области  на ось
на ось 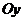 есть отрезок [0,2]. Таким образом,
есть отрезок [0,2]. Таким образом,
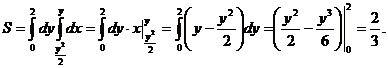
Пример 2. Вычислить площадь параболического сегмента АОВ, ограниченного дугой ВОА параболы 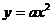 и отрезком ВА, соединяющим точки
и отрезком ВА, соединяющим точки 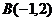 и
и 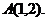
Ясно, что уравнение параболы имеет вид 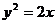 (
( 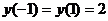 ). Фигура
). Фигура  , площадь которой надо вычислить, ограничена снизу параболой
, площадь которой надо вычислить, ограничена снизу параболой 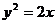 , а сверху - прямой
, а сверху - прямой 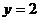 . Следовательно,
. Следовательно,
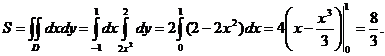
Пример 3. Вычислить площадь фигуры, ограниченной кривой
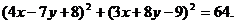
Вычисления по формуле
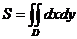
не применимы ввиду сложности пределов интегрирования. Произведем замену переменных по формулам
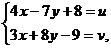 откуда
откуда 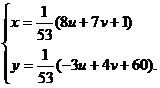
При этом 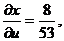
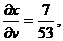
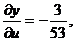
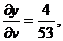 т. е.
т. е.
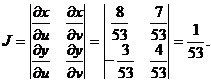
В плоскости координат 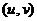 соответствующая линия имеет вид
соответствующая линия имеет вид 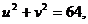 т.е. представляет собой окружность, а область
т.е. представляет собой окружность, а область 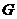 - круг
- круг 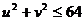 с площадью
с площадью 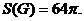 Используя соответствующие формулы, получаем
Используя соответствующие формулы, получаем
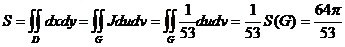 .
.
Пример 4. Вычислить площадь фигуры, ограниченной кривыми
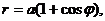
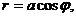 (а>0).
(а>0).
Линии даны в полярных координатах, поэтому воспользуемся формулой площади в полярных координатах
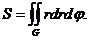
Первая функция 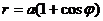 определена при
определена при 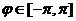 , а вторая
, а вторая 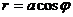 - при
- при 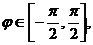 так как при прочих значениях
так как при прочих значениях  получается r<0. Соответствующая область имеет вид, изображенный на рис.14. Ввиду симметрии фигуры относительно полярной оси можно ограничиться вычислением половины площади, а результат удвоить.
получается r<0. Соответствующая область имеет вид, изображенный на рис.14. Ввиду симметрии фигуры относительно полярной оси можно ограничиться вычислением половины площади, а результат удвоить.
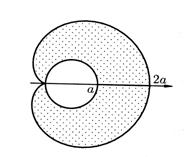
Рис. 14.
Имеем
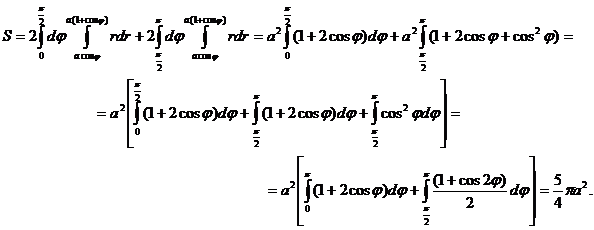
Пример 5. Вычислить объем тела, ограниченного поверхностями 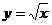 ,
, 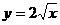 ,
, 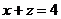 ,
, 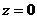 .
.
Первые два уравнения изображают параболические цилиндры с вертикальной образующей, третье, т. е. 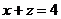 - уравнение наклонной плоскости, а уравнение
- уравнение наклонной плоскости, а уравнение 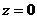 - плоскость
- плоскость  . Соответствующее тело изображено на рис. 15; сверху его ограничивает поверхность
. Соответствующее тело изображено на рис. 15; сверху его ограничивает поверхность 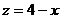 .
.
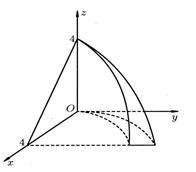 Рис. 15. Рис. 15. | 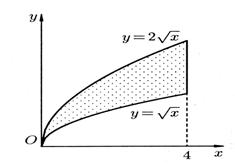 Рис. 16. Рис. 16. |
Объем тела вычислим по формуле
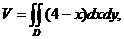
где область  изображена на рис. 16. Имеем
изображена на рис. 16. Имеем
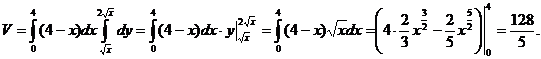
Пример 6. Вычислить объем тела, ограниченного поверхностями 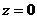 ,
, 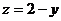 ,
, 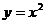 .
.
Тело, объем которого нужно вычислить, изображено на рис. 17. В силу симметрии тела относительно плоскости 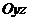 , вычислим объем половины тела и результат удвоим. Координаты точек А и В удовлетворяют системе уравнений
, вычислим объем половины тела и результат удвоим. Координаты точек А и В удовлетворяют системе уравнений 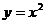 и
и 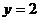 , откуда
, откуда 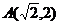 ,
, 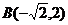 .
.
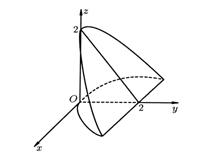
Рис.17.
Следовательно,
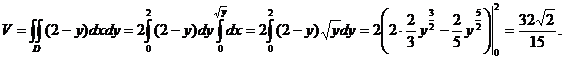
Пример 7. Вычислить площадь поверхности сферы 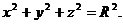
Сфера симметрична относительно координатных плоскостей, поэтому будем вычислять площадь поверхности той части, которая расположена в первом октанте, а результат умножим на 8. Запишем поверхность верхней полусферы явно, т. е. в виде 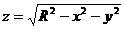 , и воспользуемся соответствующей формулой. Имеем:
, и воспользуемся соответствующей формулой. Имеем:
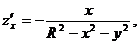
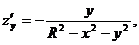
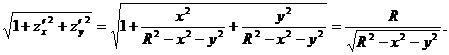
Переходя к полярным координатам 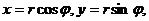 найдем искомую площадь
найдем искомую площадь
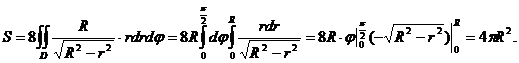
Пример 8. Определить массу круглой пластины радиуса R с центром в начале координат, если поверхностная плотность материала пластины в точке 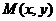 равна
равна 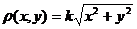 , где k>0 – фиксированное число.
, где k>0 – фиксированное число.
Переходя от прямоугольных координат к полярным, имеем
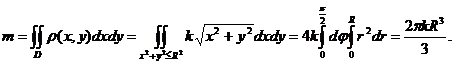
Пример 9. Найти массу круглой пластины 
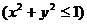 с поверхностной плотностью
с поверхностной плотностью 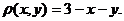
Имеем:
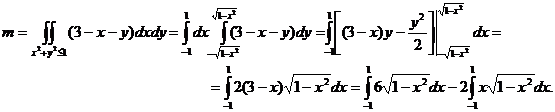
Последний интеграл равен нулю, как интеграл от нечетной функции по симметричному отрезку относительно начала координат. Поэтому, делая подстановку 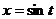 , получим
, получим
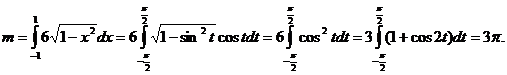
Пример 10. Найти моменты инерции квадратной пластины 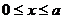 ,
, 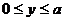 относительно осей координат и начала координат, если плотность пластины пропорциональна ординате точки пластины с коэффициентом k.
относительно осей координат и начала координат, если плотность пластины пропорциональна ординате точки пластины с коэффициентом k.
Вычисления производим по соответствующим формулам этого параграфа учитывая, что 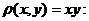
1) 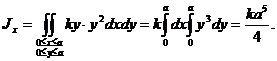
2) 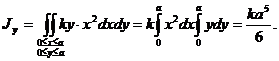
3) 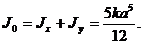
Пример 11. Найти координаты центра тяжести пластины, ограниченной параболой 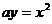 и прямой
и прямой 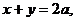 если плотность пластины постоянна и равна
если плотность пластины постоянна и равна 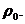
Сделаем чертеж (рис. 18). Находим абсциссы точек А и В пересечения прямой 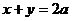 и параболы
и параболы 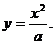 Из системы уравнений
Из системы уравнений 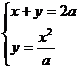 находим
находим 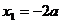 и
и 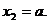
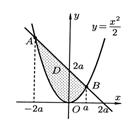
Рис. 18.
1). Масса пластины  равна
равна
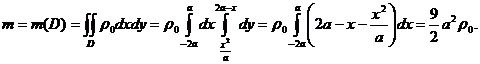
2). Вычислим статические моменты пластины относительно координатных осей
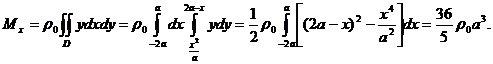
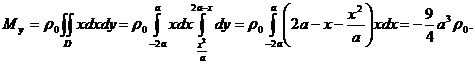
3). Координаты центра тяжести найдем теперь по формулам
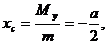
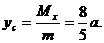
Контрольные вопросы:
- Приведите формулу для вычисления ограниченной области D плоскости Оху.
- По какой формуле вычисляется масса плоской пластины с плотностью распределения масс
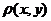 ?
? - Приведите формулу для вычисления момента инерции
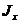 плоской материальной пластины
плоской материальной пластины  с поверхностной плотностью
с поверхностной плотностью 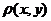 относительно оси
относительно оси 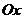 .
. - По какой формуле вычисляется статический момент пластины
 относительно оси
относительно оси 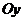 .
. - Приведите формулы для вычисления координат центра тяжести материальной пластины
 с плотностью
с плотностью 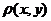 .
.
