Двойной интеграл. Свойства и методы вычисления

Двойной интеграл. Свойства и методы вычисления

Определение и геометрический смысл двойного интеграла

Пусть - некоторая замкнутая ограниченная область на плоскости , а - произвольная функция, определенная и ограниченная в этой области. Разобьем область произвольно на n непересекающихся частей , с площадями (i=1,2,…,n) (рис.1). В каждой части выберем произвольную точку и составим сумму

,

которую назовем интегральной суммой для функции 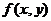в области .

Рис. 1

Обозначим через d наибольшее расстояние между граничными точками области .

Если интегральная сумма при имеет конечный предел, равный I, то этот предел называется двойным интегралом от функции 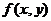по области и обозначается одним из следующих символов:

; или .

Функция 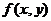- интегрируемая в области , - область интегрирования, x и y – переменные интегрирования, ds (или dxdy) – элемент площади.

Если функция 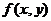непрерывна в области , то она интегрируема.

Теорема 1. Если и непрерывна в области , то интеграл

,

выражает объем тела, ограниченного снизу областью , сверху – поверхностью , а с боков – цилиндрической поверхностью, образующие которой параллельны оси , а направляющей служит граница области . (рис. 2).

В этом заключается геометрический смысл двойного интеграла.

Рис. 2.

В частности, если , то равен площади области :

.

Свойства двойного интеграла

1. Линейность. Если функции 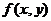и непрерывны на области , то

(α и β – постоянные числа).

2. Монотонность. Если функции 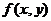и непрерывны на области и всюду в этой области , то

.

Таким образом, неравенства можно почлено интегрировать.

В частности, если , то

,

где - площадь области . Данные неравенства называются оценкой интеграла. Еще одно следствие: если на области , то

.

3. Теорема о среднем значении.

Если функция 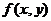непрерывна на области , то существует точка такая, что

, или .

При этом значение , т. е. число

,

называется интегральным средним значением функции 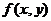в области .

4. Аддитивность. Если область представляется в виде объединения двух областей и без общих внутренних точек, то

.

5. Для любой функции 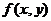, непрерывной на области , имеет место неравенство

.

Применения двойного интеграла

Двойные интегралы используются при решении многих геометрических и физических задач: вычисление площадей плоских фигур и поверхностей, объемов тел, координат центра тяжести, момента инерции и т. д.

Тройной интеграл. Свойства, вычисление, применение

Замена переменных в тройном интеграле

Цилиндрические координаты

Цилиндрические координаты (рис. 20) представляют собой обобщение полярных координат на плоскости и связаны с прямоугольными координатами формулами

, , .

Переход к тройному интегралу в цилиндрических координатах осуществляется по формуле

.

В частности, если положить в этом равенстве , то получим формулу для объема тела в цилиндрических координатах:

.

Сферические координаты

Сферические координаты , , связаны с прямоугольными координатами при помощи формул (рис. 21)

Рис. 21.

В общем случае переменные , , изменяются в пределах , . Формула перехода к сферическим координатам имеет вид

Положив , получим формулу для объема тела в сферических координатах:

Двойной интеграл. Свойства и методы вычисления