Условия существования двойного интеграла

1. Нижняя и верхняя суммы Дарбу

Как и в одномерном случае, при изучении двойного интеграла существенную роль играют суммы Дарбу.

Пусть функция z= f(x;y) ограничена на области Р. Пусть Т – произвольное разбиение области Р на части P_k , . Тогда f(x;y) будет ограничена на всех P_k. Следовательно, существуют нижние и верхние грани функции f на P_k. Обозначим , .

"(x;y)ÎP_k справедливо неравенство , 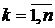. Cоставим суммы

- нижняя, - верхняя суммы Дарбу.

и зависят только от разбиения Т (не зависят от выбора точек 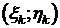, как S(T)).

Свойства сумм Дарбу

1) Для любого фиксированного разбиения Т справедливо

.

2) , .

3) Если к линиям разбиения добавить новую линию, то получим разбиение T₁, которое называется продолжением разбиения T. От этого нижняя сумма может только возрасти, а верхняя - уменьшиться.

.

4) Для любых разбиений Т₁ и Т₂ справедливо .

(Доказательство свойств 1)–4) аналогично доказательствам тех же свойств сумм Дарбу для случая одной переменной, только вместо точек деления надо брать линии).

5) Рассмотрим два числовых множества . Множество ограничено сверху любым числом из множества (по свойству4), тогда . Значит, выполнено . Из последнего неравенства следует, что множество ограничено снизу, – нижняя граница. Следовательно, и выполнено ( - наибольшая нижняя граница ). Очевидно, . Тогда выполнено .

2. Необходимое и достаточное условие интегрируемости

Теорема 2.Для того чтобы ограниченная функция z=f(x;y) была интегрируема на замкнутой квадрируемой области Р необходимо и достаточно, чтобы

. (1)

Доказательство.

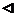1) Необходимость. Пусть функция f интегрируема на Р. Докажем (1).

Так как f интегрируема на Р, то . Это по определению означает, что "e>0 $d>0: "Т: l<d, выполнено

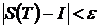. (2)

(2) Û I-e<S(T)<I+e.

Т.к. "Т , , то

. (3)

Тогда .

Т.е. для выбранного e>0 $d>0: "Т: l<d выполнено . По определению предела это значит, что выполнено (1).

2) Достаточность. Пусть f ограничена на Р и выполнено (1). Докажем, что f интегрируема на Р. "e>0 $d>0: "Т: l<d Þ

. (4)

По свойству 5) сумм Дарбу "Т:

. (5)

Из (4) и (5) Þ . Это означает, что .

Тогда . (6)

Согласно свойству 1) сумм Дарбу

. (7)

Тогда из (4), (6), (7) получим

,

,

. Значит, по определению f(x;y) интегрируема на Р.

Замечание. Отметим, что из (3) следует

,

,

т.е. при доказательстве необходимости мы установили, что если f интегрируема на P, то

.

3. Интегрируемость непрерывной функции

Теорема 3. Если функция z=f(x;y) непрерывна на замкнутой квадрируемой области Р, то она интегрируема на этой области.

Доказательство.

Пусть Т – произвольное разбиение области Р на части P_k . Т.к. z=f(x;y) непрерывна на замкнутой области Р, то f ограничена на Р и, значит, ограничена на . Следовательно, можно построить .

, (8)

где - соответственно верхние и нижние грани функции f(x;y) на области P_k. Т.к. f(x;y) непрерывна на замкнутой области Р_k, то она достигает верхней и нижней граней , т.е.

.

Подставим в (8):

. (9)

Т.к. функция f непрерывна на замкнутой области P, то она равномерно непрерывна на этой области (теорема Кантора), т.е по определению

(10)

выполнено . (11)

Пусть -произвольное число. Выберем разбиение Т так, чтобы l<d=d(e). Тогда . Значит, для точек выполнено (10). Следовательно, для значений функции в них выполнено (11):

. (12)

Из (9) и (12) следует

.

Т.о., "T: l<d выполнено . По определению это значит, что . Тогда согласно теореме 2 f интегрируема на P.

Теорема 4. Если ограниченная на P функция f имеет точки разрыва лишь на конечном числе кривых, являющихся графиками непрерывных функций вида y=f(x) или х=j(у), то она интегрируема на P, и при этом значения функции в точках разрыва не влияют на значения двойного интеграла.

(без доказательства).