Случай криволинейной области.
Областью, стандартной относительно оси OX, будем называть множество вида 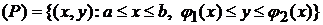 , где
, где 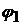 и
и 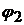 непрерывные на
непрерывные на 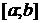 функции. Геометрически такая область характеризуется тем, что
функции. Геометрически такая область характеризуется тем, что 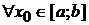 прямая
прямая 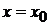 пересекает границу этой области не более, чем в двух точках.
пересекает границу этой области не более, чем в двух точках.
Аналогично определяется область, стандартная относительно оси OY:
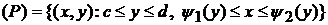 .
.
Для стандартных областей справедливы формулы:
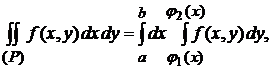 (4.5)
(4.5)
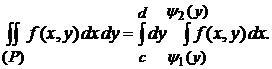 (4.6)
(4.6)
Представления (4.3), (4.4), (4.5), (4.6) двойных интегралов в виде повторных называют расстановкой пределов интегрирования в определенном порядке. Так, например, из формул (4.5) и (4.6) следует, что 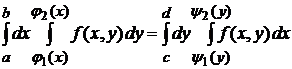 , то есть для такой области пределы интегрирования можно расставлять как в том, так и в другом порядке.
, то есть для такой области пределы интегрирования можно расставлять как в том, так и в другом порядке.
Если область интегрирования  не является стандартной, но ее можно разбить на части
не является стандартной, но ее можно разбить на части 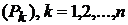 , каждая из которых является стандартной областью, то, в силу свойства аддитивности двойного интеграла,
, каждая из которых является стандартной областью, то, в силу свойства аддитивности двойного интеграла, 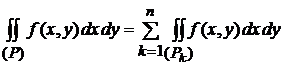 .
.
Для того, чтобы разбить область на части, являющиеся стандартными и найти соответствующие функции 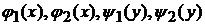 полезно изобразить область интегрирования на чертеже.
полезно изобразить область интегрирования на чертеже.
Пример 4.2. Расставить пределы интегрирования в том и другом порядке в двойном интеграле 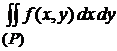 , где область
, где область  ограничена прямой
ограничена прямой 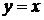 и параболой
и параболой 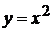 .
.
Для вычисления двойного интеграла по этой области можно воспользоваться как формулой (4.5), так и (4.6), ибо граница области  пересекается не более чем в двух точках прямыми параллельными оси OX, так и прямыми, параллельными оси OY. Применим сначала формулу
пересекается не более чем в двух точках прямыми параллельными оси OX, так и прямыми, параллельными оси OY. Применим сначала формулу
(4.5), 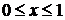 . Чтобы найти пределы для
. Чтобы найти пределы для 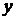 : возьмем на оси OX произвольную точку
: возьмем на оси OX произвольную точку 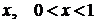 , и проведем через нее прямую, параллельную оси OY в направлении этой оси. Точка входа этой прямой области
, и проведем через нее прямую, параллельную оси OY в направлении этой оси. Точка входа этой прямой области  лежит на прямой
лежит на прямой 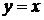
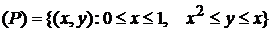 .
. 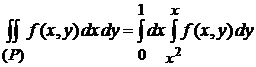 .
.
Применим теперь к двойному интегралу формулу (4.6), 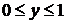 . Для того, чтобы установить, каковы будут пределы внутреннего интеграла по
. Для того, чтобы установить, каковы будут пределы внутреннего интеграла по 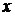 , возьмем произвольную точку
, возьмем произвольную точку 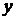 на оси OY,
на оси OY, 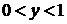 , и проведем через нее прямую, параллельную оси OX, в направлении этой оси. Точка входа этой прямой в область
, и проведем через нее прямую, параллельную оси OX, в направлении этой оси. Точка входа этой прямой в область  лежит на прямой
лежит на прямой 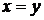 , а точка выхода ее из области лежит на параболе
, а точка выхода ее из области лежит на параболе 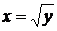 .
.
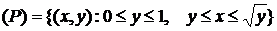 . Следовательно, согласно формуле (4.6)
. Следовательно, согласно формуле (4.6) 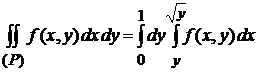 .
.
Пример 4.3. Изменить порядок интегрирования в повторном интеграле
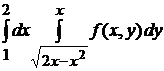 .
.
Нам не задана непосредственно область интегрирования, и мы должны выяснить ее вид по пределам повторного интеграла. Так как внутренний интеграл берется по 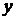 , то пределы внутреннего интеграла показывают, какими линиями область
, то пределы внутреннего интеграла показывают, какими линиями область  ограничена снизу и сверху.
ограничена снизу и сверху.
Уравнения этих линий соответственно 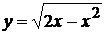 и
и 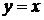 . Первое уравнение преобразуется к виду
. Первое уравнение преобразуется к виду 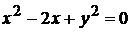 , или
, или 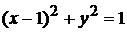 и определяет верхнюю половину окружности с центром в точке (1;0) радиуса 1. Так как при
и определяет верхнюю половину окружности с центром в точке (1;0) радиуса 1. Так как при 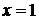
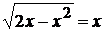 , то прямая
, то прямая 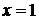 , ограничивающая область слева, пересекает ее в одной точке (1;1). Прямая
, ограничивающая область слева, пересекает ее в одной точке (1;1). Прямая 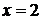 , ограничивающая область интегрирования справа, пересекает окружность в точке касания (2;0), а прямую
, ограничивающая область интегрирования справа, пересекает окружность в точке касания (2;0), а прямую 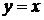 -- в точке (2;2). Начертим область интегрирования
-- в точке (2;2). Начертим область интегрирования  . Граница области
. Граница области  состоит из участков трех линий:
состоит из участков трех линий:
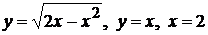 . Из рисунка видно, что точки входа в область
. Из рисунка видно, что точки входа в область  одних прямых, параллельных оси OX, лежат на дуге окружности
одних прямых, параллельных оси OX, лежат на дуге окружности 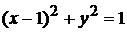 , а других – на биссектрисе
, а других – на биссектрисе 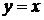 . Точки выхода из области
. Точки выхода из области  всех этих прямых лежат на прямой
всех этих прямых лежат на прямой 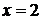 . Поэтому область
. Поэтому область
интегрирования  разобьем на две части
разобьем на две части 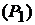 и
и 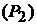 . Тогда точки входа в область
. Тогда точки входа в область 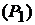 всех прямых, параллельных оси OX, будут лежать только на дуге окружности
всех прямых, параллельных оси OX, будут лежать только на дуге окружности 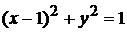 , а в область
, а в область 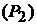 -- только на биссектрисе
-- только на биссектрисе 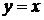 . Решая уравнения этих линий относительно
. Решая уравнения этих линий относительно 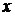 , получим
, получим
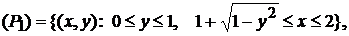
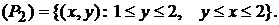
Учитывая все сказанное, имеем
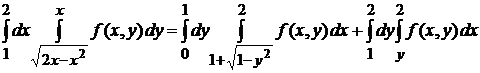 .
.
Пример 4.4. Вычислить 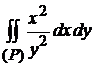 , где
, где  -- область, ограниченная прямыми
-- область, ограниченная прямыми 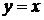 ,
, 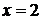 и гиперболой
и гиперболой 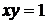 .
.
Решая совместно уравнения прямой 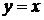 и гиперболой
и гиперболой 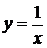 , получим точку их пересечения А(1;1). Для вычисления интеграла по заданной области удобно воспользоваться формулой (4.5). В этом случае мы будем иметь дело с одним повторным интегралом, так как прямые, параллельные оси OY,
, получим точку их пересечения А(1;1). Для вычисления интеграла по заданной области удобно воспользоваться формулой (4.5). В этом случае мы будем иметь дело с одним повторным интегралом, так как прямые, параллельные оси OY,
Входят в область  на гиперболе
на гиперболе 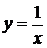 и выходят из нее на прямой
и выходят из нее на прямой 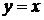 . Легко видеть, что обратный порядок интегрирования, то есть применение формулы (4.6), был бы хуже, так привел бы к сумме двух повторных интегралов. Это объясняется тем, что область
. Легко видеть, что обратный порядок интегрирования, то есть применение формулы (4.6), был бы хуже, так привел бы к сумме двух повторных интегралов. Это объясняется тем, что область  ограничена слева разными линиями, и поэтому часть прямых, параллельных оси OX, входят в эту область на гиперболе
ограничена слева разными линиями, и поэтому часть прямых, параллельных оси OX, входят в эту область на гиперболе 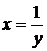 , а часть – на прямой
, а часть – на прямой 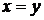 .
.
Итак, приступим к вычислению двойного интеграла.
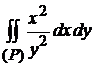 , где
, где 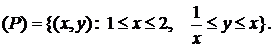
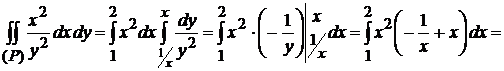
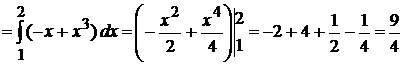 .
.
Пример 4.5. Вычислить площадь области, ограниченной параболой 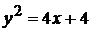 и прямой
и прямой 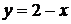 .
.
Решая систему уравнений 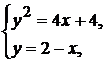 найдем точки пересечения параболы и прямой: А(0;2), В(8;-6). В силу формулы (4.1), площадь области
найдем точки пересечения параболы и прямой: А(0;2), В(8;-6). В силу формулы (4.1), площадь области 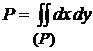 . Из рисунка видно, что вычисление двойного интеграла
. Из рисунка видно, что вычисление двойного интеграла
лучше провести по формуле (4.6), при другом порядке интегрирования мы получили бы сумму двух повторных интегралов.
Внешний интеграл по переменной 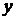 берется в пределах от -6 до 2, а пределы внутреннего интеграла находятся из уравнений параболы и прямой, если решить их относительно
берется в пределах от -6 до 2, а пределы внутреннего интеграла находятся из уравнений параболы и прямой, если решить их относительно 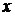 :
: 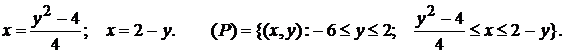
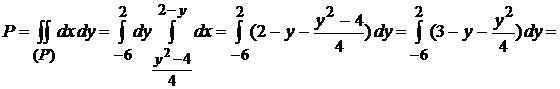
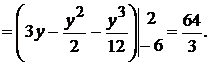
Прежде чем перейти к примерам на вычисление объемов, следует иметь ввиду следующее замечание. При вычислении объема какого-нибудь тела полезно сделать пространственный рисунок, который давал бы представление о форме данного тела. Если же рисунок не удастся построить, то можно ограничиться хотя бы рисунком, изображающим только область интегрирования (основание цилиндрического бруса на плоскости). Однако и в этом случае необходимо представит себе, какая поверхность ограничивает брус сверху, а какая – снизу.
Пример 4.6. Вычислить объем тела, ограниченного параболоидом вращения 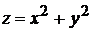 , координатными плоскостями и плоскостью
, координатными плоскостями и плоскостью 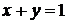 .
.
Поверхность параболоида вращения 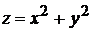 получается вращением вокруг оси OZ параболы
получается вращением вокруг оси OZ параболы 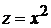 . Уравнение
. Уравнение 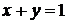 в пространстве определяет плоскость, параллельную оси OZ, и пресекающую плоскость XOY по прямой
в пространстве определяет плоскость, параллельную оси OZ, и пресекающую плоскость XOY по прямой 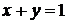 в этой плоскости.
в этой плоскости.
На рисунке изображено тело, объем которого надо вычислить. Это тело сверху ограничено поверхностью параболоида 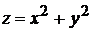 , снизу – плоскостью XOY, спереди –
, снизу – плоскостью XOY, спереди –
плоскостью 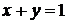 , слева – плоскостью XOZ (y=0), справа – плоскостью YOZ (x=0). Это тело представляет собой цилиндрический брус, расположенный над плоскостью
, слева – плоскостью XOZ (y=0), справа – плоскостью YOZ (x=0). Это тело представляет собой цилиндрический брус, расположенный над плоскостью
XOY. Его объем будем вычислять по формуле (4.2). Область интегрирования  --
--
прямоугольный треугольник. 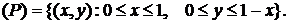
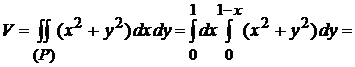
Упражнения
4.1. Изменить порядок интегрирования.
1)  7)
7) 
2)  8)
8) 
3)  9)
9) 
4)  10)
10) 
5)  11)
11) 
6)  12)
12) 
13)  .
.
4.2. Вычислить двойные интегралы (указаны линии, ограничивающие область интегрирования).
1) 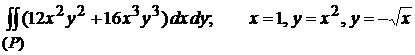 (1)
(1)
2) 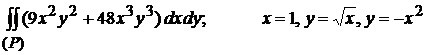 (2)
(2)
3) 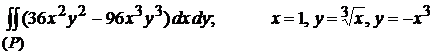 (1)
(1)
4) 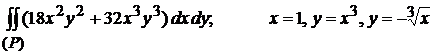 (1)
(1)
5) 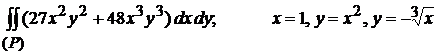 (2)
(2)
6) 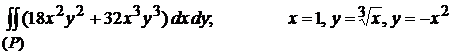 (3)
(3)
7) 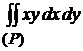
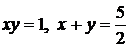
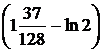
8) 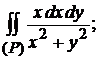
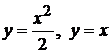
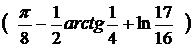
9) 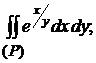
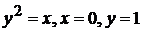

10) 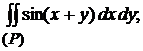
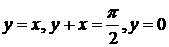

11) 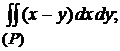
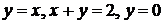

12) 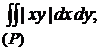
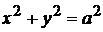
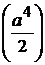
13) 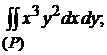
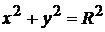 (0)
(0)
Замечание к задачам 12, 13.
Если функция 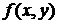 четна относительно переменной
четна относительно переменной 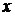 в области
в области  , то есть
, то есть 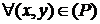
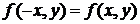 (аналогично относительно
(аналогично относительно 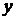 ), то
), то
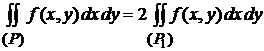 , где
, где 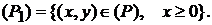
Если 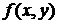 нечетна относительно переменной
нечетна относительно переменной 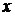 в области
в области  , то есть
, то есть 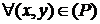
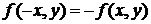 , то
, то 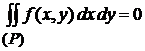 .
.
