Механический смысл несобственного интеграла.
Если 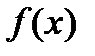 непрерывна и неотрицательна на промежутке
непрерывна и неотрицательна на промежутке 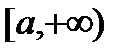 , то
, то 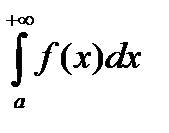 есть масса стержня
есть масса стержня 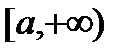 с плотностью
с плотностью 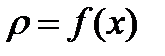 .
.
Пример. Вычислить 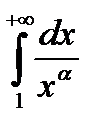
1) Пусть 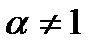 , тогда
, тогда 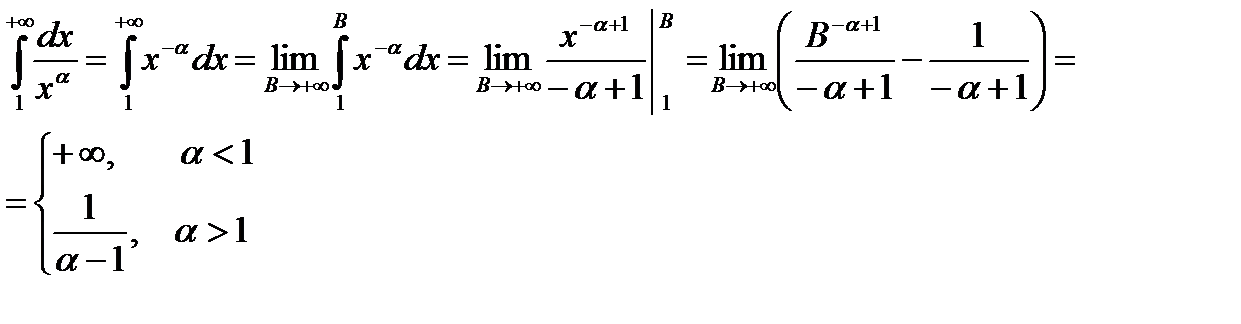
2) 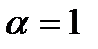 ;
; 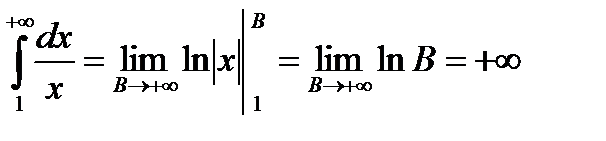 .
.
Следовательно, при 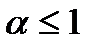 несобственный интеграл
несобственный интеграл 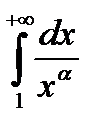 расходится, а при
расходится, а при 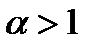 сходится.
сходится.
Пример. Вычислить интеграл 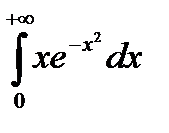 .
.
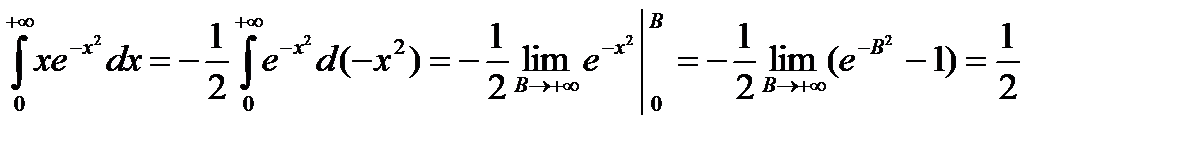 .
.
Пример. Вычислить 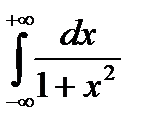
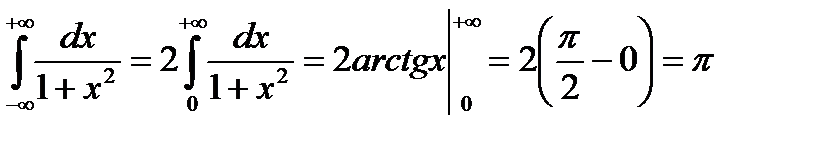
7.2.2. Несобственные интегралы от функций, заданных на конечном отрезке 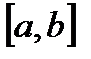 , но неограниченных на этом отрезке.
, но неограниченных на этом отрезке.
Пусть функция 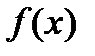 непрерывна в промежутке
непрерывна в промежутке 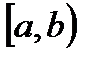 и неограниченна на этом промежутке.
и неограниченна на этом промежутке.
Рассмотрим произвольное 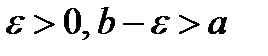 .
.
Интеграл 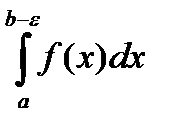 существует, т.к.
существует, т.к. 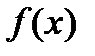 непрерывна на отрезке
непрерывна на отрезке 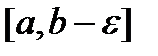 .
.
Несобственный интеграл 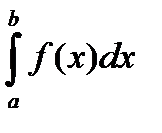 определяется следующим равенством
определяется следующим равенством
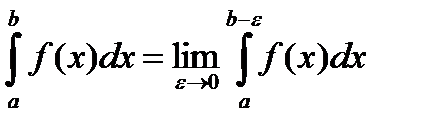 .
.
Если 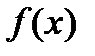 непрерывна в промежутке
непрерывна в промежутке 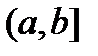 и неограниченна на нем, то несобственный интеграл
и неограниченна на нем, то несобственный интеграл 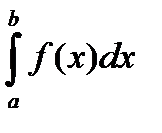 определяется аналогично предыдущему интегралу:
определяется аналогично предыдущему интегралу:
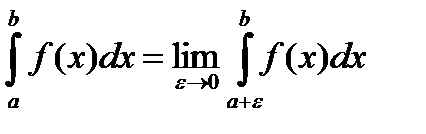 , где
, где 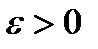 ;
; 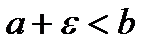 .
.
Пусть теперь 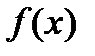 непрерывна на множестве
непрерывна на множестве 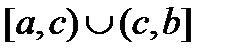 и неограниченна на этом множестве.
и неограниченна на этом множестве.
Несобственный интеграл 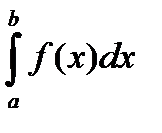 определяется следующим равенством:
определяется следующим равенством:
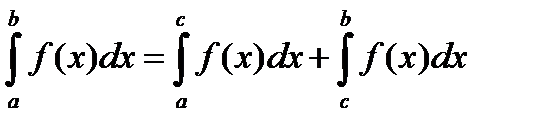 , если оба интеграла справа существуют.
, если оба интеграла справа существуют.
Далее рассмотрим случай, когда 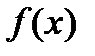 непрерывна в интервале
непрерывна в интервале 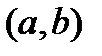 и неограниченна на этом интервале.
и неограниченна на этом интервале.
Несобственный интеграл 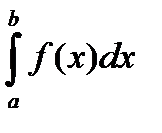 определяется равенством:
определяется равенством:
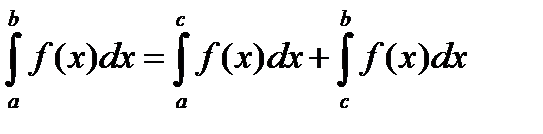 , где a<c<b, при этом оба интеграла в правой части должны существовать, т.е. должны сходиться.
, где a<c<b, при этом оба интеграла в правой части должны существовать, т.е. должны сходиться.
Можно показать, что сходимость интеграла 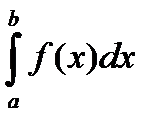 и его значение не зависят от выбора точки с.
и его значение не зависят от выбора точки с.
Пример. Вычислить интеграл 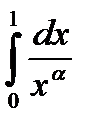 .
.
1) 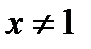
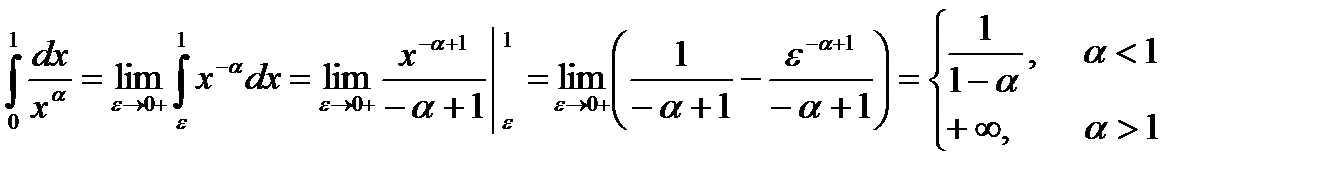
2) 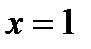
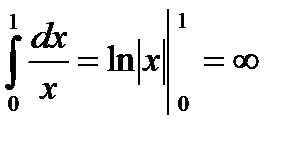 .
.
Таким образом, несобственный интеграл 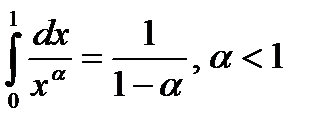 , сходится, а при
, сходится, а при 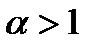 расходится.
расходится.
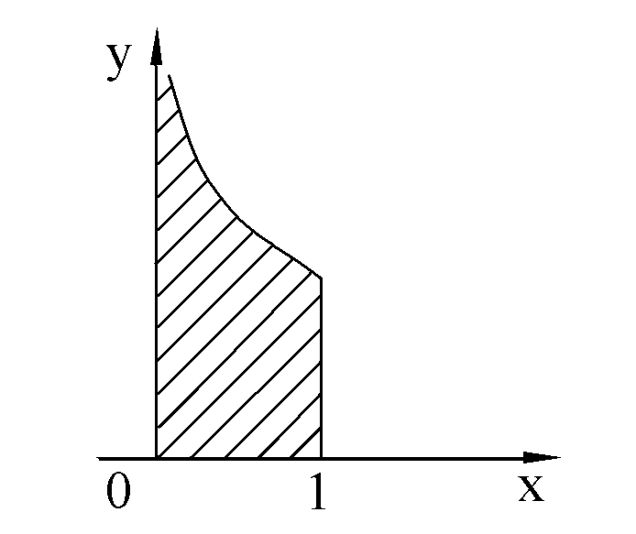
С геометрической точки зрения несобственный интеграл 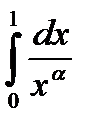 равен площади криволинейной трапеции, ограниченной осью OX, осью OY, прямой
равен площади криволинейной трапеции, ограниченной осью OX, осью OY, прямой 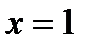 и графиком функции
и графиком функции 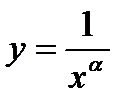 при
при 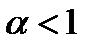 .
.
7.2.3. Признаки сходимости несобственных интегралов.
В данном пункте под несобственным интегралом 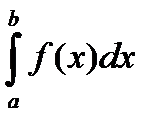 мы будем понимать какой-либо из ранее рассмотренных несобственных интегралов. В частности, a и b могут равняться
мы будем понимать какой-либо из ранее рассмотренных несобственных интегралов. В частности, a и b могут равняться 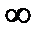 .
.
Теорема 1. Если в рассматриваемом промежутке выполняются неравенства 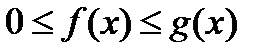 , то из сходимости несобственного интеграла
, то из сходимости несобственного интеграла 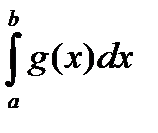 следует сходимость несобственного интеграла
следует сходимость несобственного интеграла 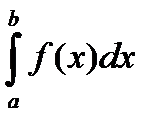 , а из расходимости интеграла
, а из расходимости интеграла 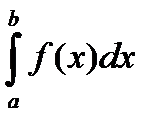 следует расходимость интеграла
следует расходимость интеграла 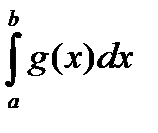 . (Без док-ва).
. (Без док-ва).
Определение. Несобственный интеграл 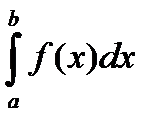 называется абсолютно сходящимся, если сходится интеграл
называется абсолютно сходящимся, если сходится интеграл 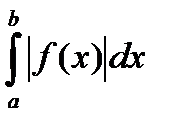 .
.
Теорема 2. Если несобственный интеграл 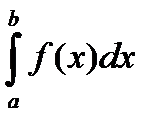 сходится абсолютно, то он сходится. (Без док-ва).
сходится абсолютно, то он сходится. (Без док-ва).
Пример. Исследовать на сходимость интеграл 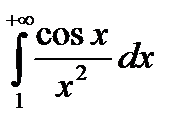 .
.
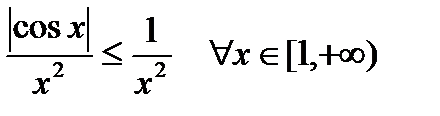
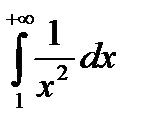 - сходится (см. п. 7.1.1.). По теореме 1 сходится интеграл
- сходится (см. п. 7.1.1.). По теореме 1 сходится интеграл 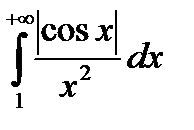 . Это означает, что данный интеграл сходится абсолютно. Следовательно, по теореме 2 данный интеграл сходится.
. Это означает, что данный интеграл сходится абсолютно. Следовательно, по теореме 2 данный интеграл сходится.
Отметим, что данные рассуждения не позволяют найти точное значение интеграла 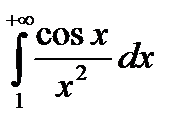 .
.
Лекция 8.
Тема: Вычисление площадей плоских фигур. Вычисление объемов тел.
8.1. Вычисление площадей плоских фигур.
8.1.1. Вычисление площади фигуры в декартовой системе координат.
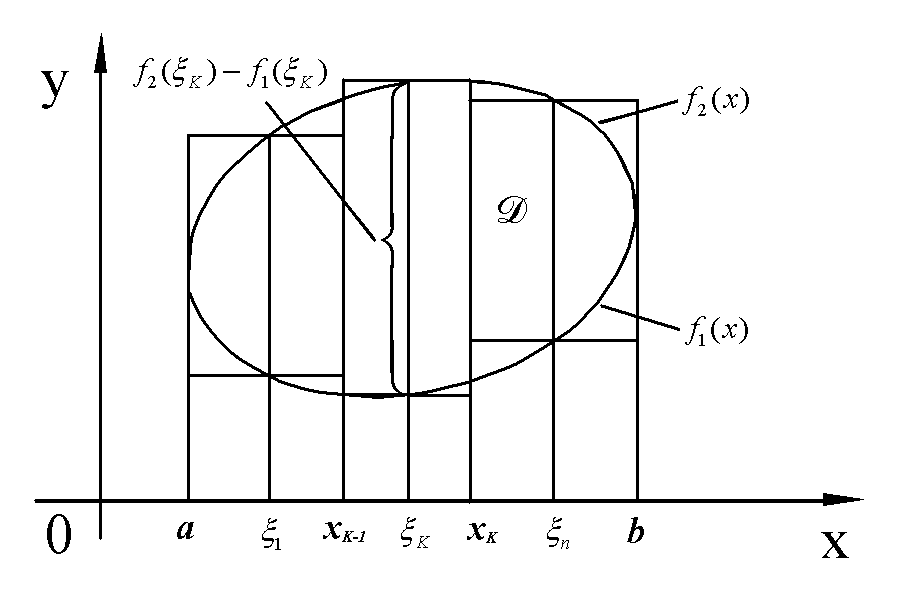
Пусть на плоскости задана ограниченная область D.
Область D проецируется на ось ОХ в отрезок 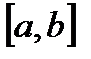 . Будем предполагать, что любая прямая
. Будем предполагать, что любая прямая 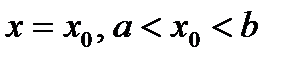 , пересекает границу области D в двух точках. Прямые
, пересекает границу области D в двух точках. Прямые 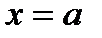 и
и 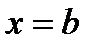 могут иметь с границей области общие отрезки.
могут иметь с границей области общие отрезки.
В данном случае можно записать уравнение кривой, ограничивающей область D снизу 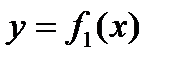 и уравнение кривой, ограничивающей область D сверху
и уравнение кривой, ограничивающей область D сверху 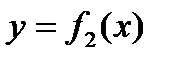 .
.
Отрезок [a,b] произвольным способом разобьем на n частей точками 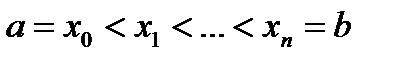 . Это разбиение обозначим через Т. Через
. Это разбиение обозначим через Т. Через 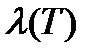 обозначим наибольшую из длин частей разбиения. Пусть
обозначим наибольшую из длин частей разбиения. Пусть 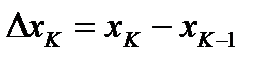 , тогда
, тогда 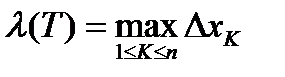 .
.
В каждой из частей разбиения произвольным способом выберем по точке 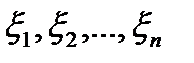 .
.
Прямые 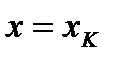 разобьют область D на n частей. К-тую часть разбиения заменим прямоугольником с основанием
разобьют область D на n частей. К-тую часть разбиения заменим прямоугольником с основанием 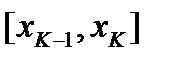 и высотой
и высотой 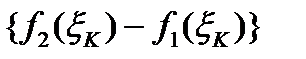 .
.
Площадь S фигуры D приближенно равна 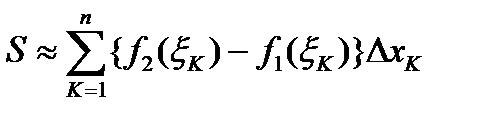 .
.
Определение. Площадью S области D называется 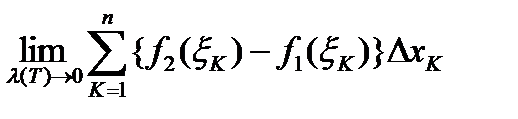 , если предел существует. Если данный предел не существует, то область D площади не имеет. Если область D имеет площадь, то она называется квадрируемой.
, если предел существует. Если данный предел не существует, то область D площади не имеет. Если область D имеет площадь, то она называется квадрируемой.
В определении площади области D сумма, стоящая под знаком предела является интегральной суммой для функции 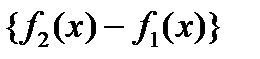 , поэтому
, поэтому 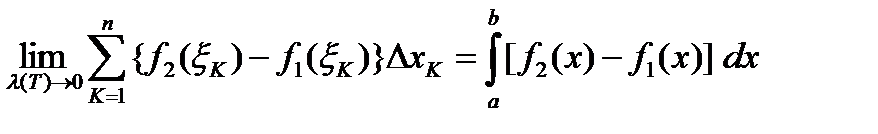 и
и
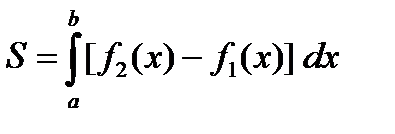 .
.
Если 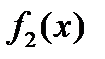 и
и 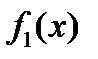 непрерывные функции на отрезке
непрерывные функции на отрезке 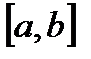 , то по теореме существования определенного интеграла можно утверждать, что область D имеет площадь, т.е. область D квадратируема.
, то по теореме существования определенного интеграла можно утверждать, что область D имеет площадь, т.е. область D квадратируема.
Замечание 1. Область D можно проецировать на ось OY на отрезок 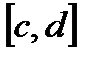 и тогда
и тогда 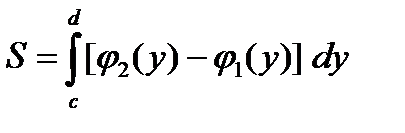 , где кривая
, где кривая 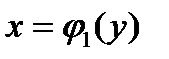 ограничивает область D снизу, а кривая
ограничивает область D снизу, а кривая 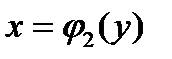 ограничивает область D сверху.
ограничивает область D сверху.
Замечание 2. Если область D такова, что сразу нельзя по предыдущим формулам вычислить площадь в области D, то область D надо разбить на конечное число частей, не имеющих общих внутренних точек, так что можно вычислить площадь каждой из частей. Тогда площадь в области D вычислится как сумма площадей частей разбиения.
Пример. Вычислить площадь фигуры, ограниченной линиями 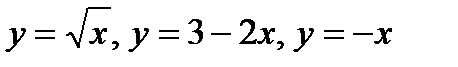 .
.
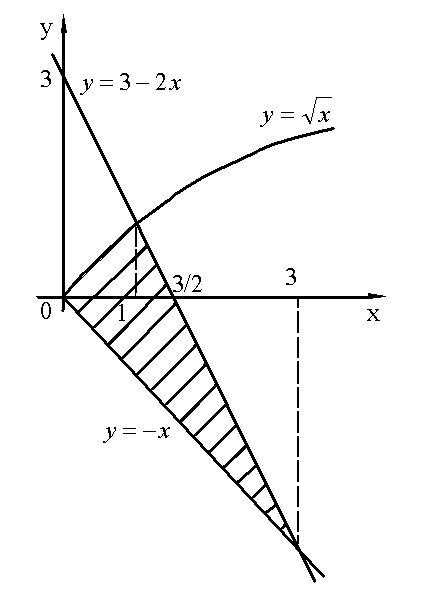
Область D проецируется на ось OX в отрезок [0,3]. Сверху область D ограничена линией 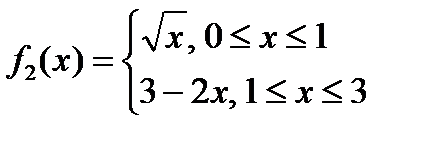
Снизу область D ограничена линией 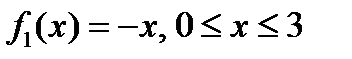 . По формуле находим:
. По формуле находим: 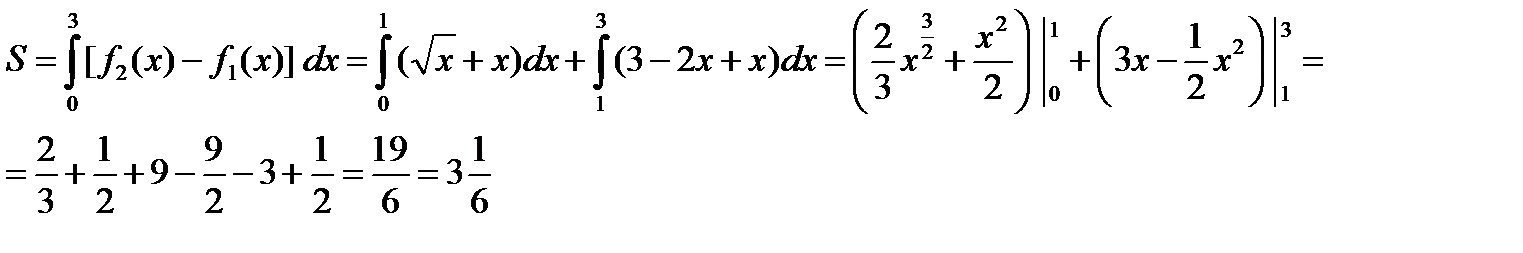
8.1.2. Вычисление площади фигуры, граница которой задана параметрически.
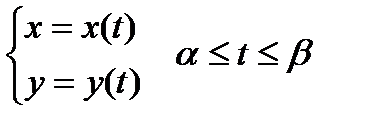
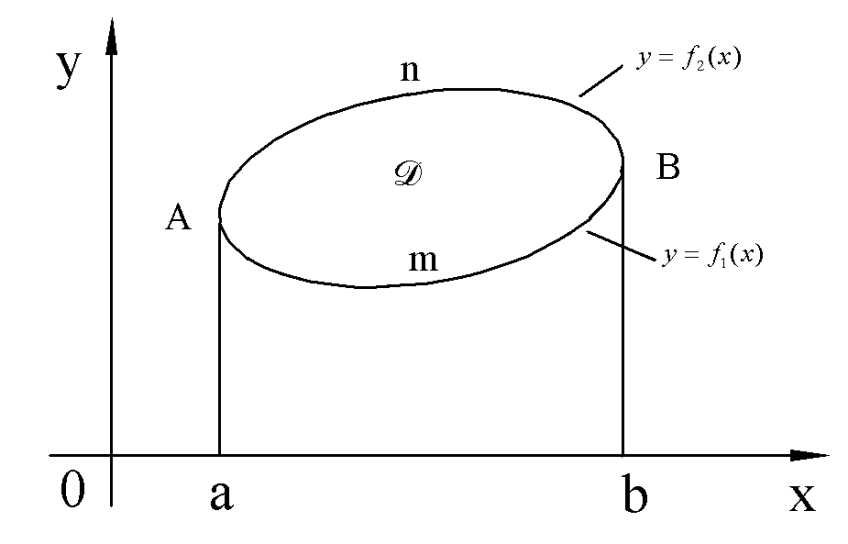
Пусть область D проецируется на ось OX в отрезок [a,b] и 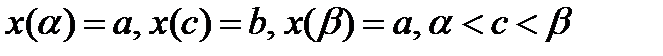 . Функция x=x(t) на промежутках
. Функция x=x(t) на промежутках 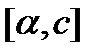 и
и 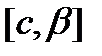 монотонна и имеет непрерывную производную.
монотонна и имеет непрерывную производную.
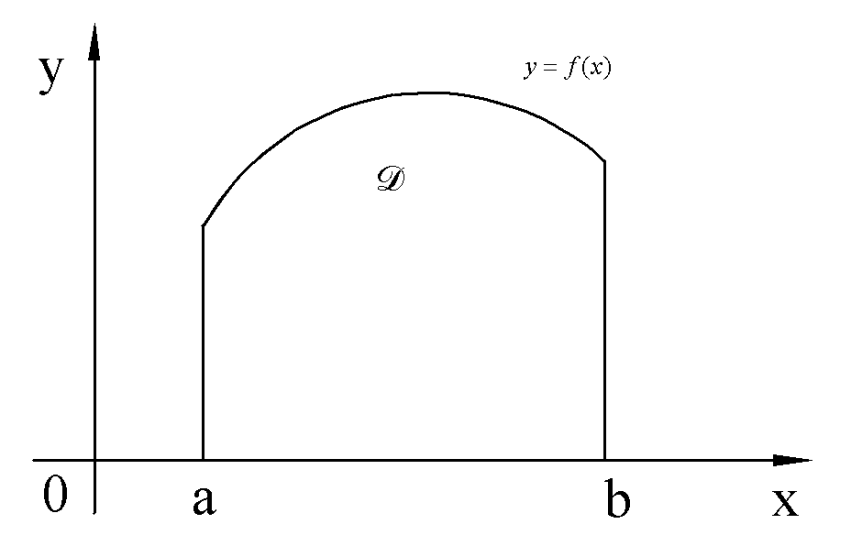
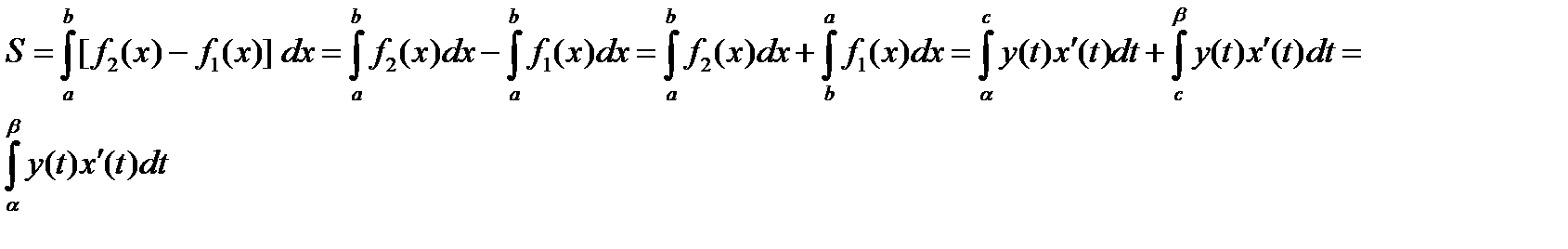 В частности, если требуется вычислить площадь криволинейной трапеции, причем уравнение верхней кривой
В частности, если требуется вычислить площадь криволинейной трапеции, причем уравнение верхней кривой 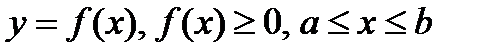 , задано параметрически
, задано параметрически
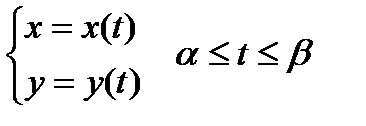 , где x(t) монотонная функция имеет непрерывную производную на
, где x(t) монотонная функция имеет непрерывную производную на 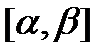 ,
, 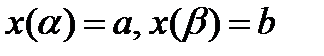 , то где
, то где 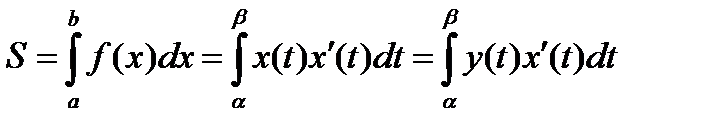 .
.
Пример. Вычислить площадь фигуры, ограниченной осью ОХ и одной аркой циклоиды
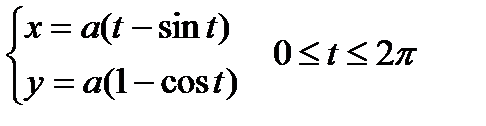
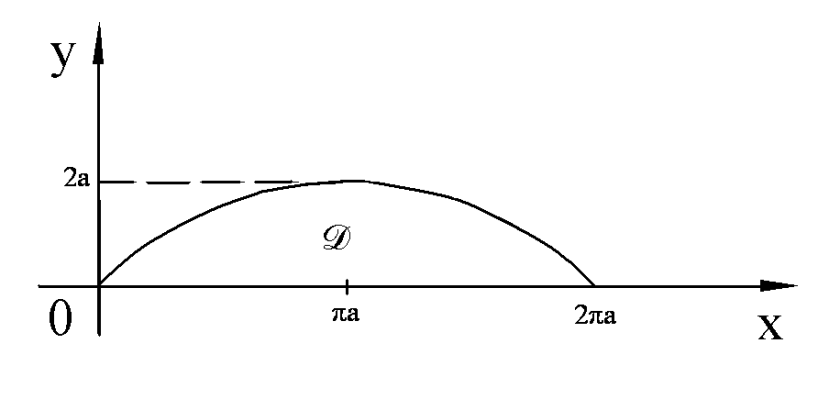
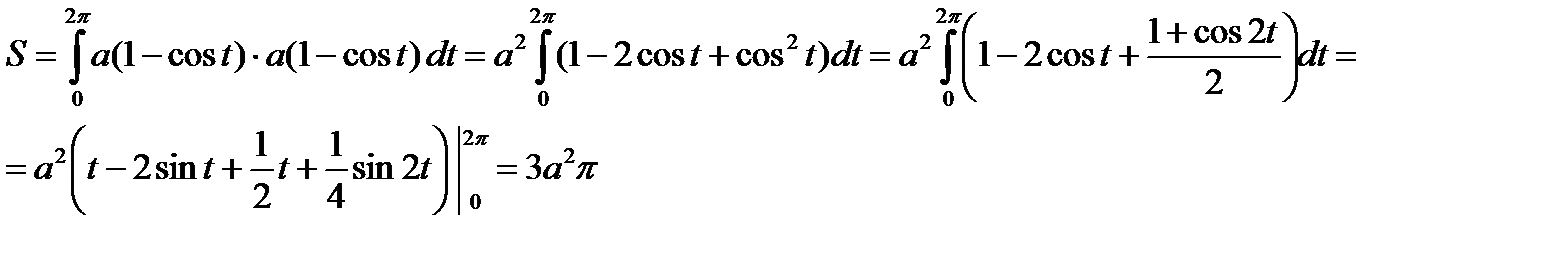
Пример. Вычислить площадь фигуры, ограниченной эллипсом 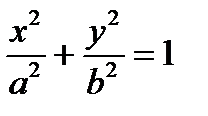 . Запишем уравнение эллипса в параметрическом виде: x=acost, y=bsint,
. Запишем уравнение эллипса в параметрическом виде: x=acost, y=bsint, 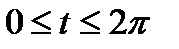
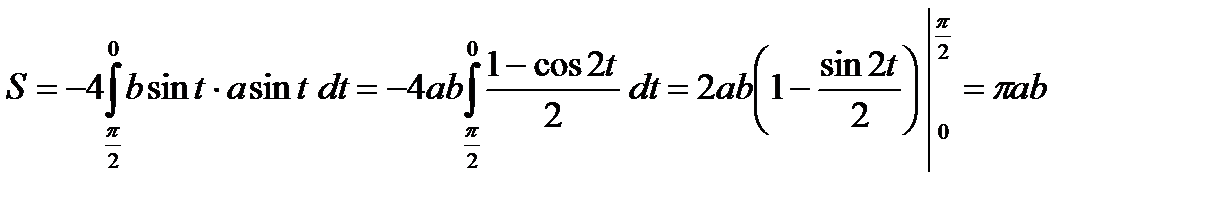 .
.
8.1.3. Вычисление площади фигуры в полярной системе координат.
Вычислим теперь площадь области D в полярной системе координат.
Пусть область D ограничена лучами 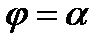 и
и 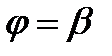 . Будем предполагать, что любой луч
. Будем предполагать, что любой луч 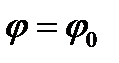 ,
, 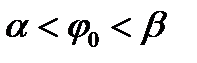 , пересекает границу области D в двух точках. В этом случае область D будет ограничена двумя линиями
, пересекает границу области D в двух точках. В этом случае область D будет ограничена двумя линиями 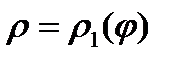 ,
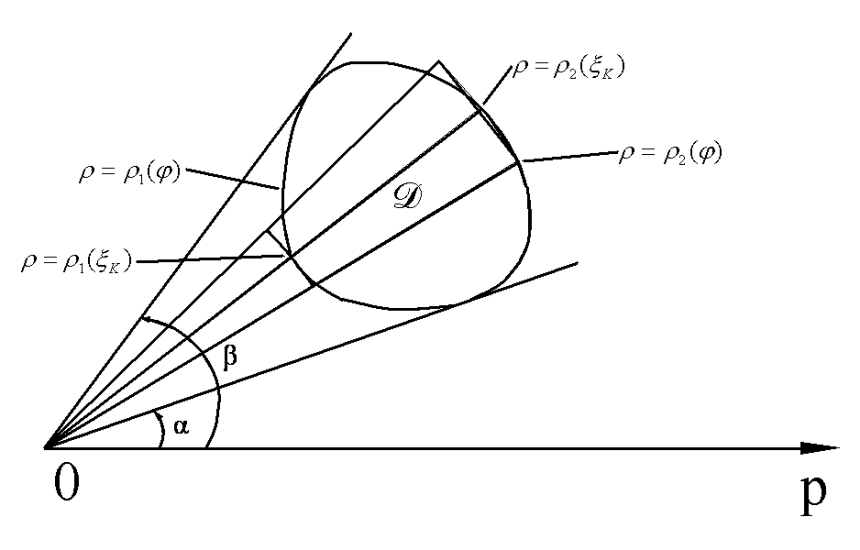
, 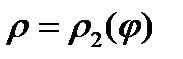 и лучами
и лучами 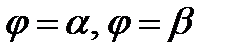 .
.
Угол между лучами 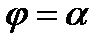 и
и 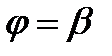 разобьем произвольным способом на n частей лучами
разобьем произвольным способом на n частей лучами 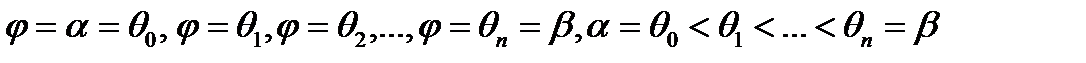 .
.
Это разбиение обозначим через (Т), 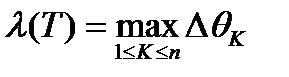 , где
, где 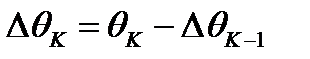 .
.
В каждом частичном угле выберем произвольным способом луч 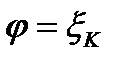 .
.
К-тому углу поставим в соответствие два круговых сектора с радиусами 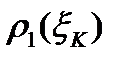 и
и 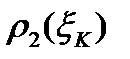 .
.
Площадь области D приближенно равна
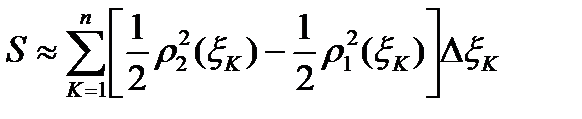 .
.
Естественно за S принять предел таких сумм при 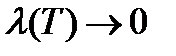 .
.
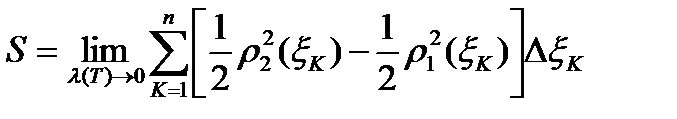
Выражение, стоящее под знаком предела, является интегральной суммой для функции 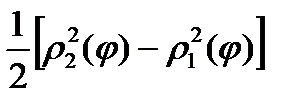 .
.
Следовательно,
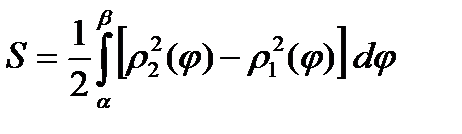 .
.
Рассмотрим два частных случая.
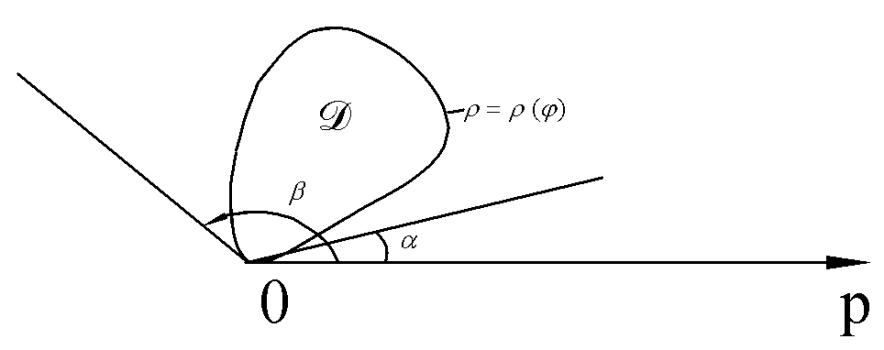
1) Пусть полюс 0 лежит на границе области D. В этом случае 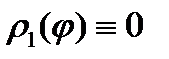 , а
, а 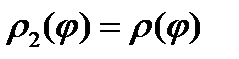 .
.
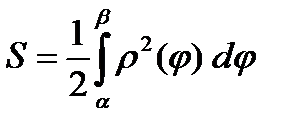
2) Пусть полюс 0 лежит внутри области D
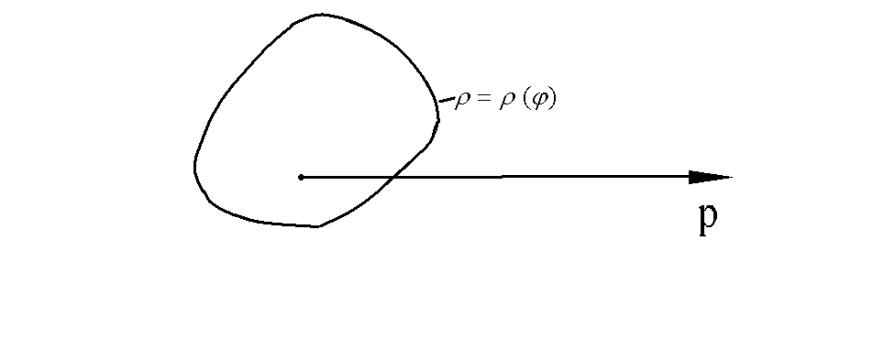
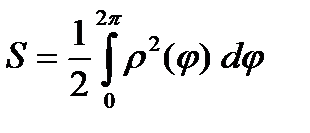
Пример. Вычислить площадь фигуры, ограниченной кардиоидой 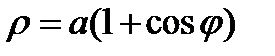
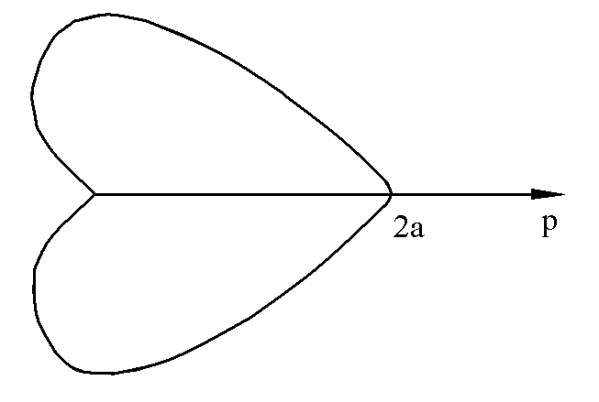
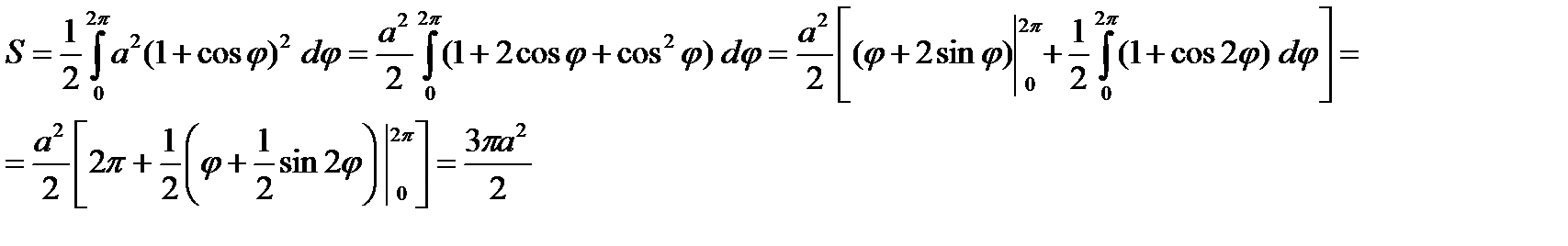
8.2. Вычисление объемов тел.
Общее определение объема тела связано с изучением двойного интеграла и будет изложено в III семестре. Сейчас мы рассмотрим некоторые частные случаи.
8.2.1. Вычисление объемов тел по площадям параллельных сечений.
Пусть в пространстве дано ограниченное тело, границей которого является замкнутая поверхность.
Данная область проецируется на ось ОХ в отрезок 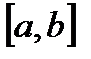 . Будем предполагать, что
. Будем предполагать, что 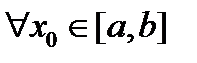 известна площадь
известна площадь 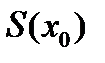 сечения данного тела плоскостью
сечения данного тела плоскостью 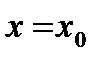 .
.
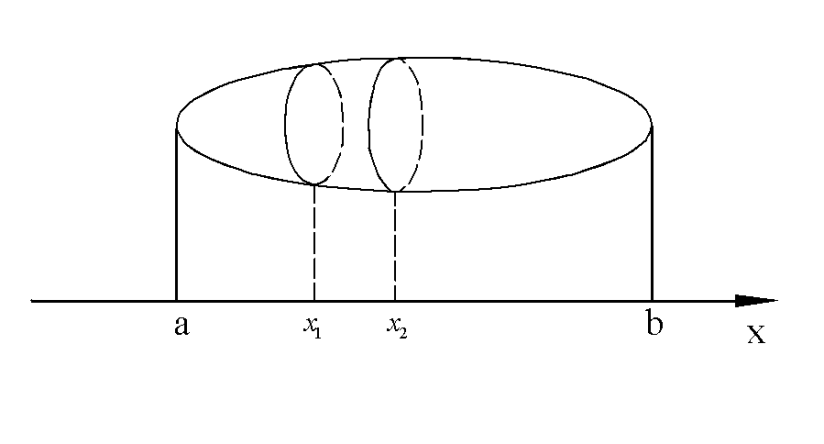
Отрезок 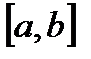 произвольным способом разобьем на n частей точками
произвольным способом разобьем на n частей точками 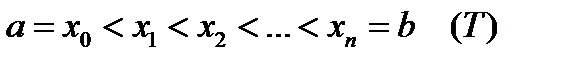 . Пусть
. Пусть 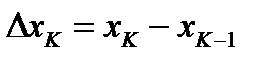 ,
, 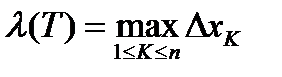 .
.
Плоскости 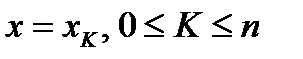 разобьют данное тело на n частей.
разобьют данное тело на n частей.
В каждом из отрезков разбиения 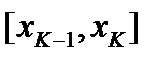 произвольным способом выберем по точке
произвольным способом выберем по точке 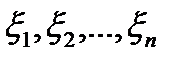 .
.
Объем К-той части разбиения данного тела приближенно равен 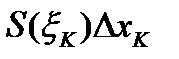 , а объем всего тела приближенно равен
, а объем всего тела приближенно равен
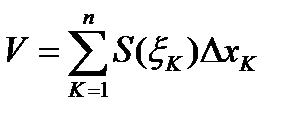 .
.
За объем тела принимают предел сумм 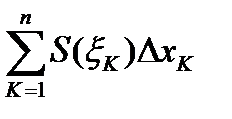 при
при 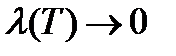 , т.е.
, т.е.
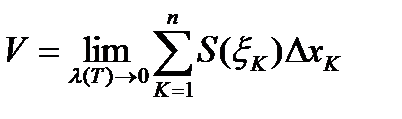 .
.
Сумма, стоящая под знаком предела, является интегральной суммой для функции s(x), поэтому
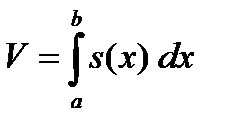 .
.
Отметим, что мы дали определение объема тела и указали способ его вычисления.
Пример. Вычислить объем тела, ограниченного эллипсоидом 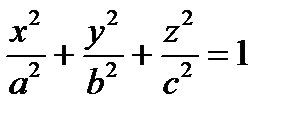 .
.
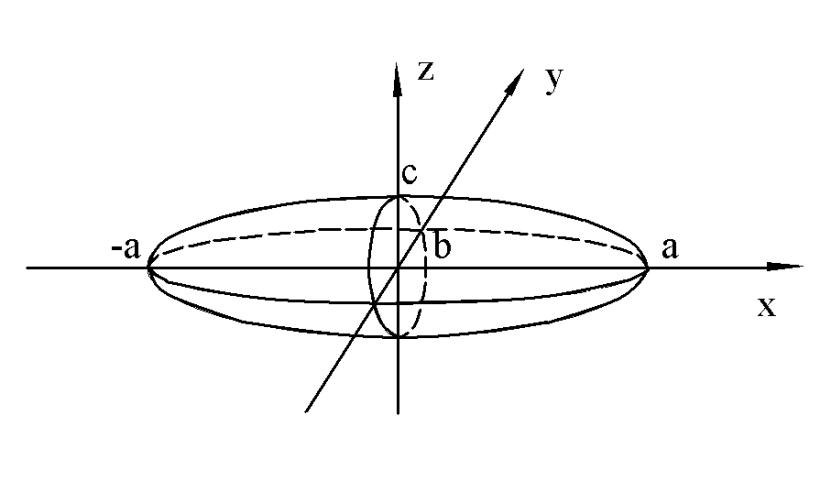
Данный эллипсоид проецируется на ось OX в отрезок 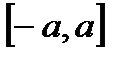 .
. 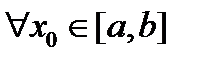 плоскость
плоскость 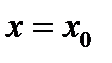 пересекает тело по области, границей которой является эллипс
пересекает тело по области, границей которой является эллипс 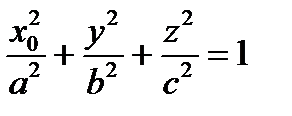 . Найдем полуоси этого эллипса
. Найдем полуоси этого эллипса 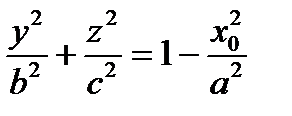 ;
; 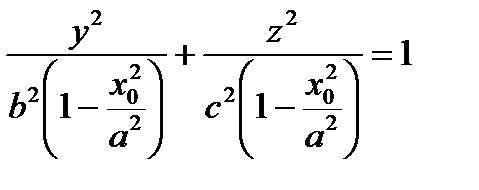 .
.
Следовательно, полуосями эллипса являются 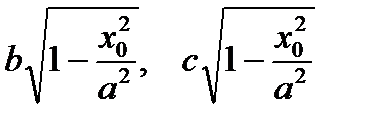
Поэтому, площадь сечения 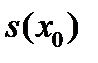 равна
равна
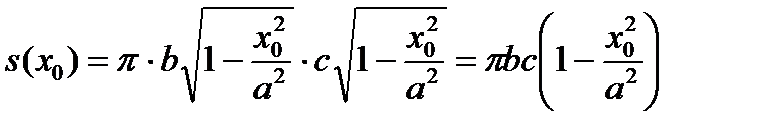 .
.
Объем тела вычисляется по формуле
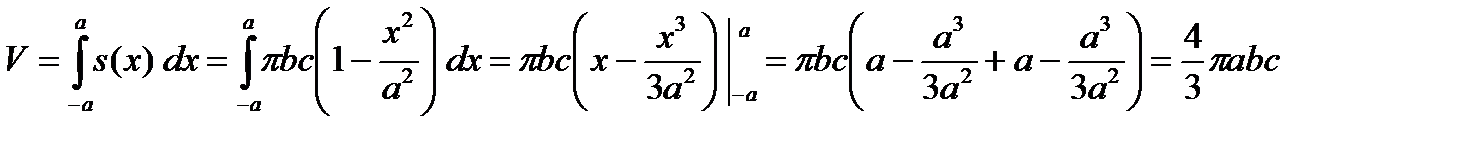 .
.
Если a=b=c, то тело, ограниченное эллипсоидом, является шаром.
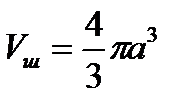 , где a – радиус шара.
, где a – радиус шара.
8.2.2. Вычисление объемов тел вращения.
Пусть тело является телом вращения криволинейной трапеции вокруг оси OX.
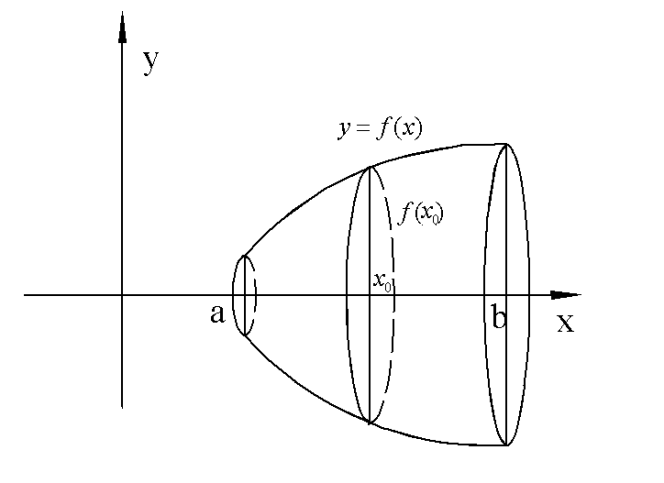
В этом случае 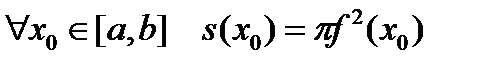 и
и 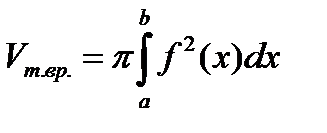 .
.
Пусть теперь тело является телом вращения фигуры D, которая не пересекает оси OX, причем любая прямая, параллельная оси OY пересекает границу D не более чем в двух точках.
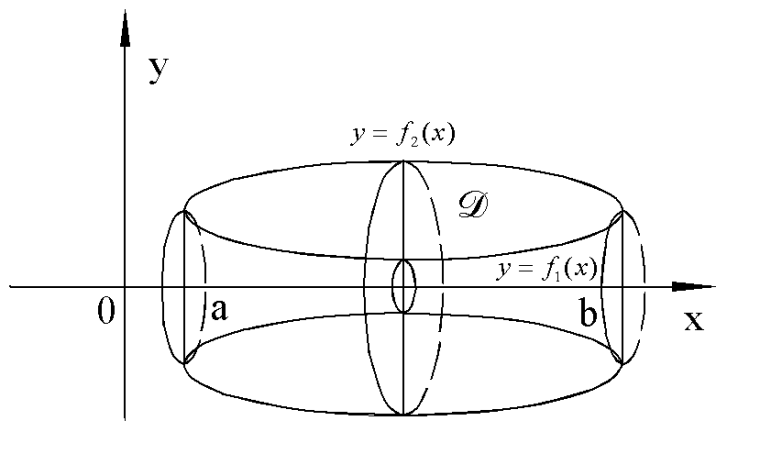
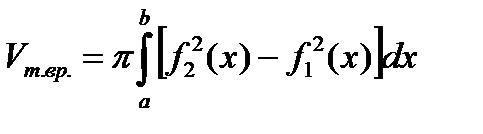 .
.
Пример. Вычислить объем тела вращения круга 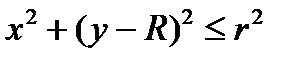 ,
, 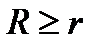 , вокруг оси OX.
, вокруг оси OX.
Такое тело называется тором.
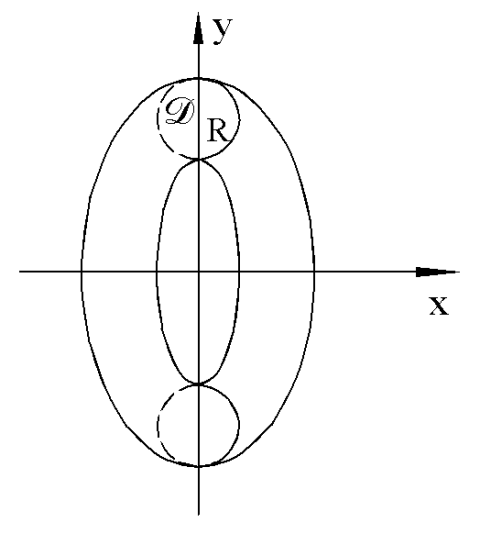
Фигура D ограничена сверху полуокружностью 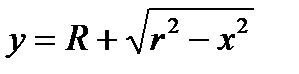 , а снизу полуокружностью
, а снизу полуокружностью 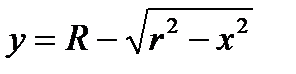 . Поэтому
. Поэтому
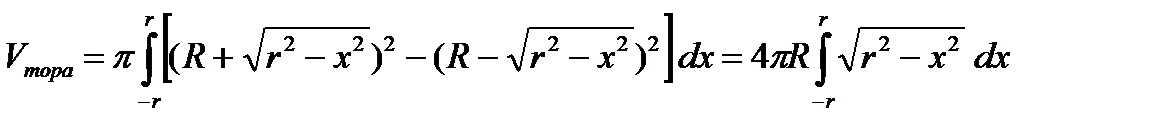
Последний интеграл есть площадь половины круга радиуса r. Поэтому 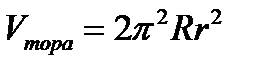 .
.
Лекция 9.
Тема: Вычисление длины кривой, площади поверхности тела вращения.
9.1. Вычисление длины кривой.
9.1.1. Пусть некоторая кривая является графиком функции 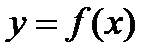 ,
, 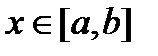 , для которой
, для которой 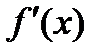 является непрерывной функцией на
является непрерывной функцией на 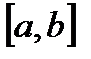 . Такие кривые называются гладкими.
. Такие кривые называются гладкими.
Во-первых, мы должны дать определение длины кривой, во-вторых, указать способ ее вычисления.
Отрезок 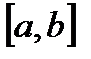 произвольным способом разобьем на n частей точками
произвольным способом разобьем на n частей точками 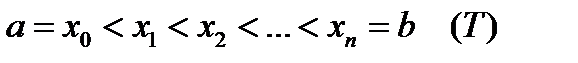
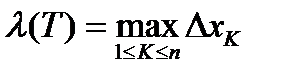
Этому разбиению будет соответствовать некоторое разбиение кривой AB на n частей точками 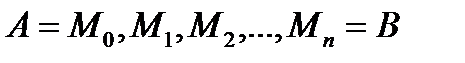 .
.
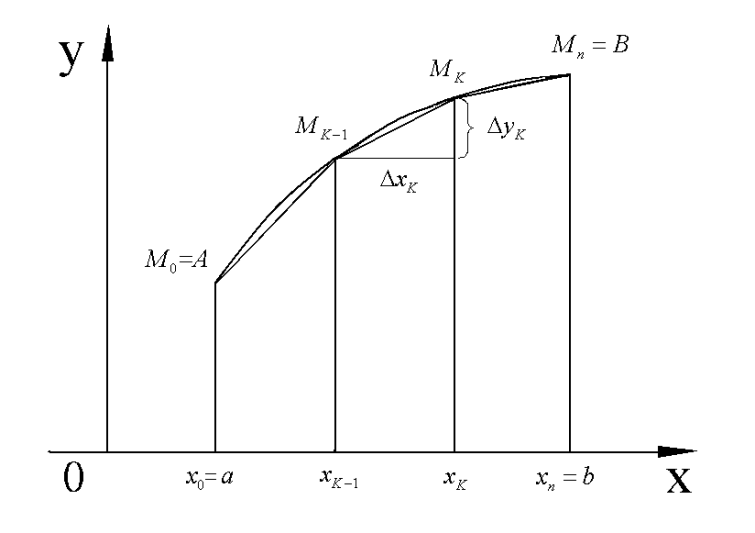
Соседние точки на кривой соединим отрезками, в результате получим ломаную 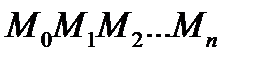 . Длина К-того участка ломаной равна
. Длина К-того участка ломаной равна 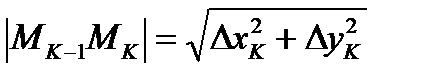 , где
, где 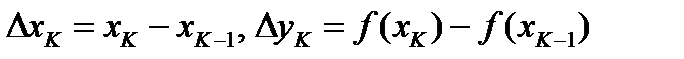 .
.
Длина l данной кривой приближенно равна длине ломаной 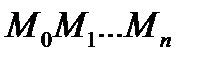 , т.е.
, т.е. 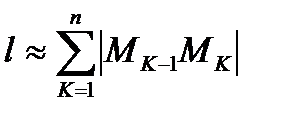 .
.
За длину кривой принимают 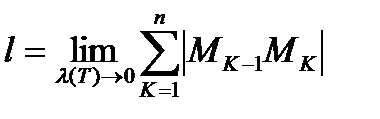 . Кривая, имеющая длину называется спрямляемой. Вычислять длину кривой с помощью определения неудобно. Далее дадим способ вычисления длины кривой с помощью определенного интеграла.
. Кривая, имеющая длину называется спрямляемой. Вычислять длину кривой с помощью определения неудобно. Далее дадим способ вычисления длины кривой с помощью определенного интеграла.
Т.к. 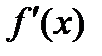 по условию непрерывна на
по условию непрерывна на 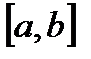 , то
, то 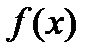 тоже непрерывна на
тоже непрерывна на 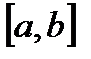 . Поэтому
. Поэтому 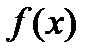 на каждом из отрезков
на каждом из отрезков 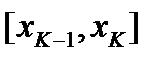 удовлетворяет всем условиям теоремы Лагранжа, по которой
удовлетворяет всем условиям теоремы Лагранжа, по которой 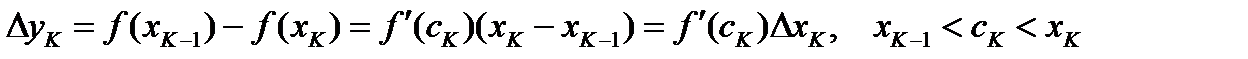 .
.
Поэтому, 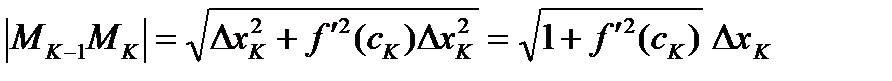 .
.
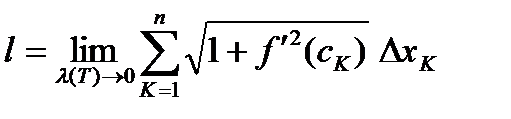 .
.
Выражение под знаком предела является интегральной суммой для функции 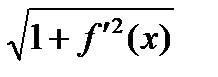 . Следовательно,
. Следовательно,
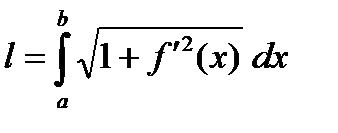 . (1)
. (1)
Мы предположили, что 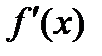 непрерывная функция на
непрерывная функция на 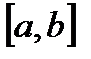 , поэтому подынтегральная функция
, поэтому подынтегральная функция 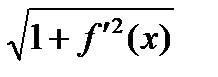 непрерывна на
непрерывна на 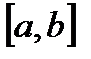 и длина такой кривой существует, т.е. кривая спрямляема.
и длина такой кривой существует, т.е. кривая спрямляема.
9.1.2. Пусть уравнение кривой задано параметрически 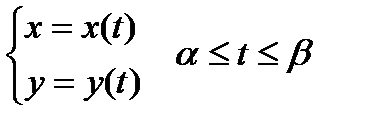 , где
, где 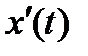 и
и 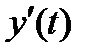 непрерывны на
непрерывны на 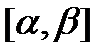 , причем
, причем 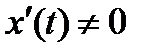 .
.
Заметим, что в равенстве (1) выражение, стоящее под знаком интеграла, есть дифференциал длины кривой: 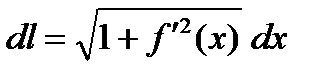 . Дифференциал длины кривой, заданной параметрически, записывается в следующем виде:
. Дифференциал длины кривой, заданной параметрически, записывается в следующем виде:
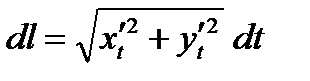 , поэтому
, поэтому
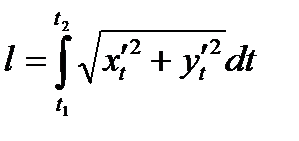 (2)
(2)
9.1.3. Рассмотрим кривую, которая задана в полярной системе координат.
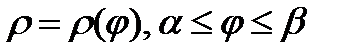 .
.
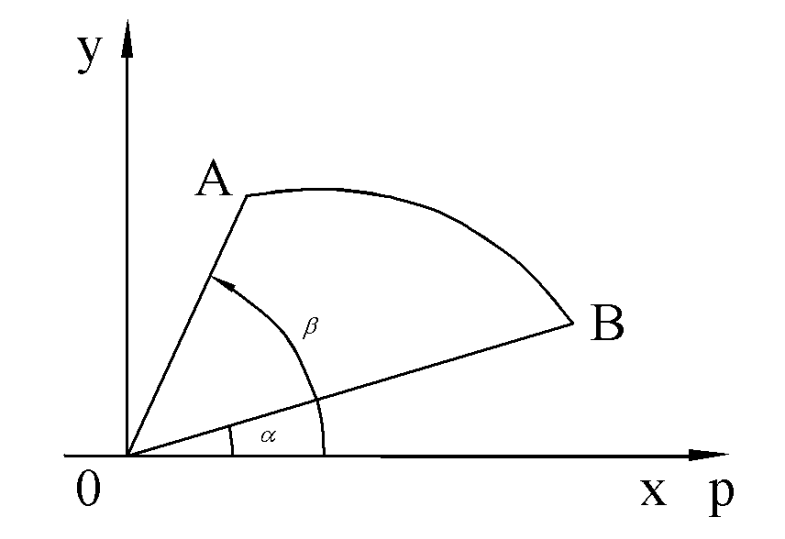
Напомним, что дифференциал дуги кривой в полярной системе координат имеет вид: 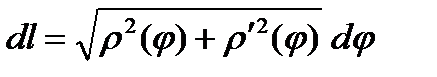 , поэтому
, поэтому
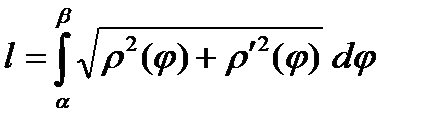 . (3)
. (3)
Пример. Вычислить длину кривой 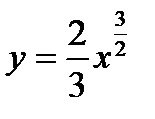 от точки
от точки 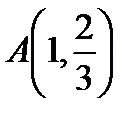 до точки
до точки 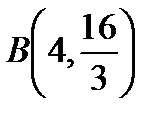
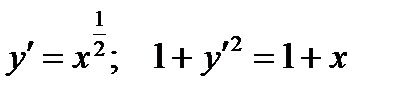
По формуле (1) получаем:
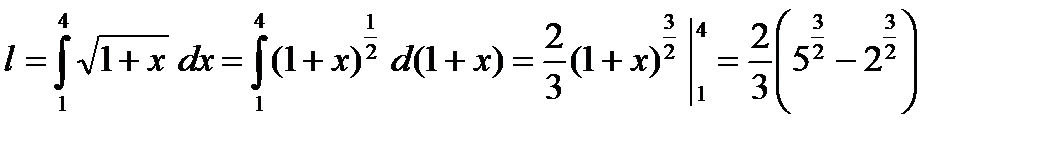
Пример. Вычислить длину одной арки циклоиды 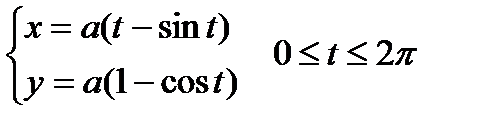
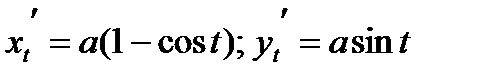
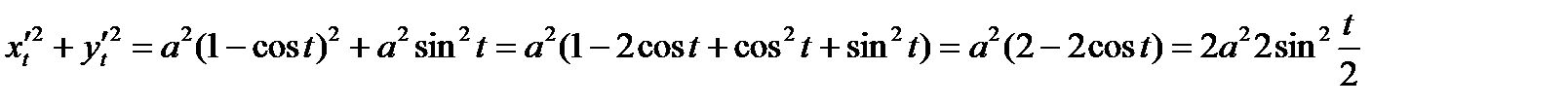 .
.
По формуле (2) получаем
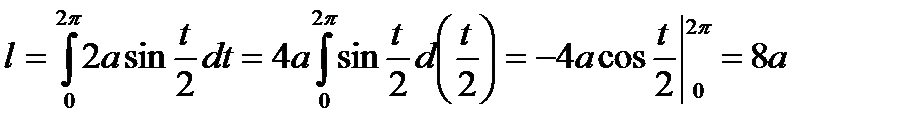
Пример. Вычислить длину кардиоиды
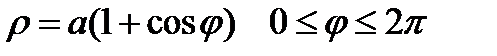
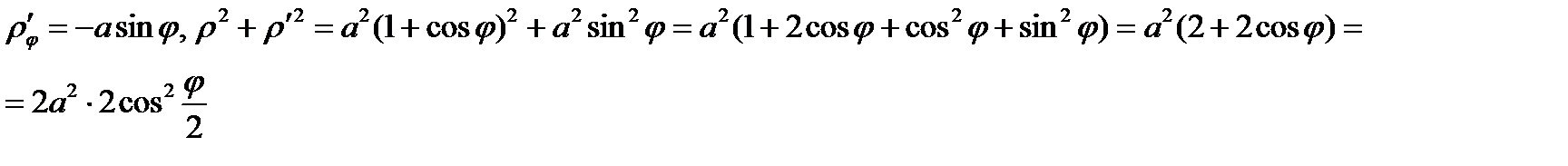

Т.к. кардиоида симметрична относительно поляры OP, то достаточно найти длину кардиоиды при 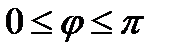 , а затем удвоить.
, а затем удвоить.
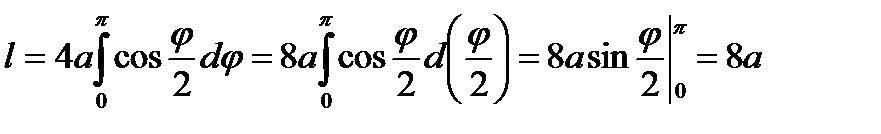 .
.
9.2. Вычисление площади поверхности тела вращения.
Пусть кривая AB задана параметрически
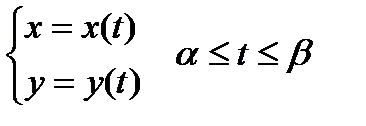 , (4)
, (4)
где 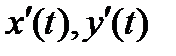 непрерывны на отрезке
непрерывны на отрезке 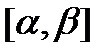 . В этом случае кривая AB спрямляема, т.е. имеет длину, которую обозначим µ. Точка A имеет координаты
. В этом случае кривая AB спрямляема, т.е. имеет длину, которую обозначим µ. Точка A имеет координаты 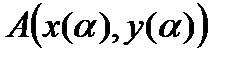 . Рассмотрим на кривой AB точку M с координатами
. Рассмотрим на кривой AB точку M с координатами 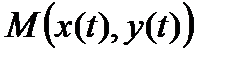 . Дуга AM спрямляема, т.к. вся кривая AB спрямляема. Пусть l(t) длина дуги AM. Функция l(t) возрастает с возрастанием t. Через t=t(l) обозначим обратную функцию. Подставляя это значение в уравнение (4), получим:
. Дуга AM спрямляема, т.к. вся кривая AB спрямляема. Пусть l(t) длина дуги AM. Функция l(t) возрастает с возрастанием t. Через t=t(l) обозначим обратную функцию. Подставляя это значение в уравнение (4), получим:
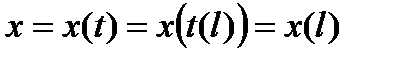 (5)
(5)
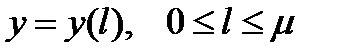 , т.е. мы имеем параметрическое представление кривой, где за параметр принимается длина кривой l. Такое представление кривой бывает удобным во многих вопросах математики.
, т.е. мы имеем параметрическое представление кривой, где за параметр принимается длина кривой l. Такое представление кривой бывает удобным во многих вопросах математики.
Пусть кривая AB задана уравнениями (5).
Дадим определение площади поверхности тела вращения.
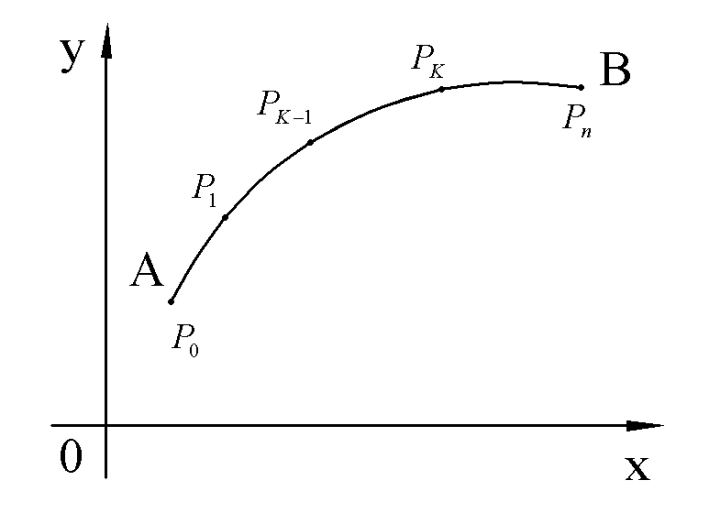
Отрезок 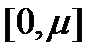 произвольным способом разобьем на n частей точками
произвольным способом разобьем на n частей точками
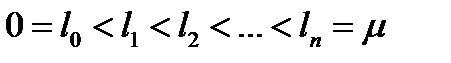
Это разбиение обозначим через (T). 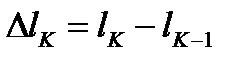 ,
, 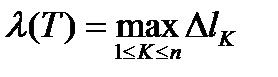 . Точкам
. Точкам 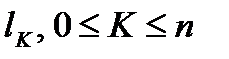 , на кривой AB будут соответствовать точки
, на кривой AB будут соответствовать точки 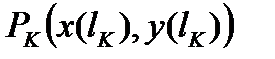 . Полученные соседние точки соединим отрезками
. Полученные соседние точки соединим отрезками 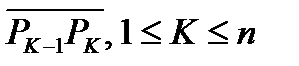 , в результате получим ломаную
, в результате получим ломаную 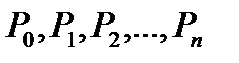 . Через S(T) обозначим площадь поверхности вращения ломаной вокруг оси OX.
. Через S(T) обозначим площадь поверхности вращения ломаной вокруг оси OX.
Определение. Площадью S поверхности вращения кривой AB вокруг оси OX называется предел площади S(T) при 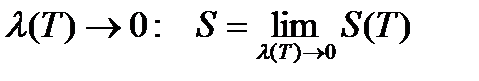 .
.
Далее выведем формулу, позволяющую вычислять площадь поверхности вращения с помощью определенного интеграла.
С этой целью подсчитаем площадь S(T). Через 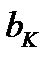 обозначим длину отрезка
обозначим длину отрезка 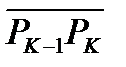 . Поверхность вращения этого отрезка есть усеченный конус, радиусы основания которого равны
. Поверхность вращения этого отрезка есть усеченный конус, радиусы основания которого равны 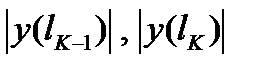 , а длина образующей равна
, а длина образующей равна 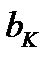 . Следовательно, площадь поверхности К-того усеченного конуса равна
. Следовательно, площадь поверхности К-того усеченного конуса равна
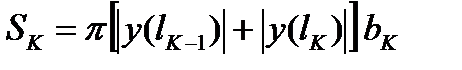 , а
, а 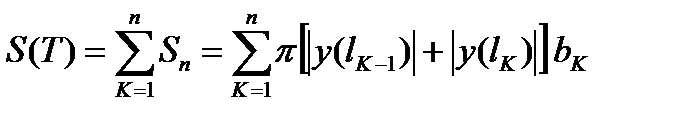 (6)
(6)
Правая часть равенства (6) не является интегральной суммой, т.к. 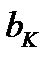 не является приращением аргумента l.
не является приращением аргумента l.
Выражение для S(T) преобразуем следующим образом:
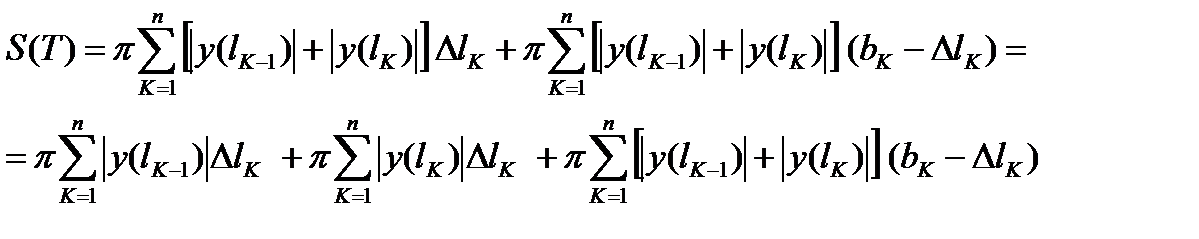 (7)
(7)
Суммы 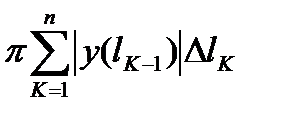 ,
, 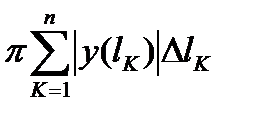 являются интегральными суммами для непрерывной функции
являются интегральными суммами для непрерывной функции 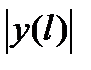 . Поэтому
. Поэтому
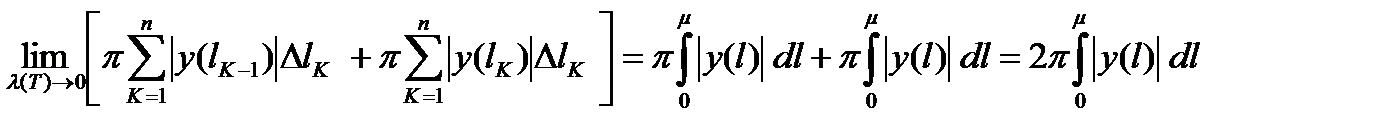 .
.
Покажем теперь, что предел последней суммы в равенстве (7) равен нулю при 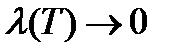 . Функция
. Функция 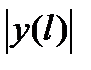 непрерывна и поэтому она ограничена:
непрерывна и поэтому она ограничена: 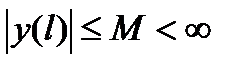 .
.
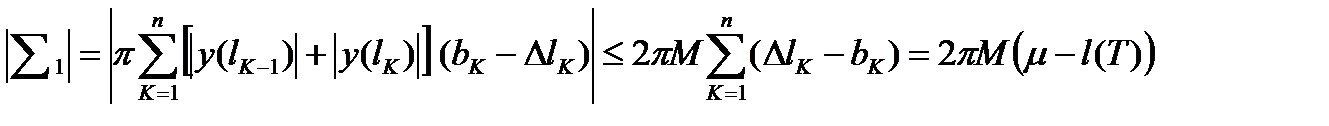 , (8)
, (8)
где µ - длина кривой, а l(T), как и ранее, длина ломаной.
Отсюда
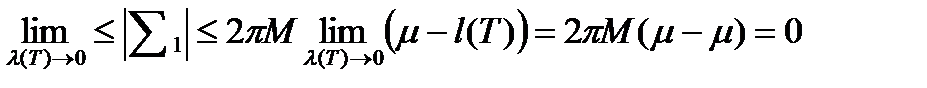 (9)
(9)
Из равенств (7), (8) и (9) следует:
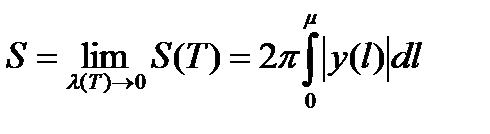 .
.
Это и есть формула для вычисления площади поверхности вращения. При применении этой формулы надо найти длину кривой µ и найти функцию 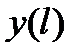 , что представляет определенные неудобства.
, что представляет определенные неудобства.
Для получения формулы, свободной от этих недостатков, перейдем к исходному заданию кривой в параметрической форме (4). Под знаком интеграла сделаем замену переменной:
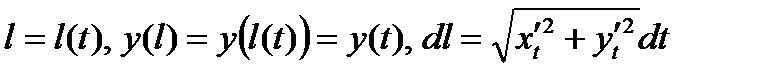 , тогда будем иметь:
, тогда будем иметь:
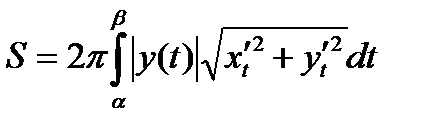 .
.
В частности, если уравнение кривой задано в явном виде 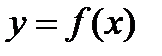 ,
, 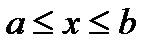 ,
, 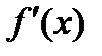 - непрерывна, то
- непрерывна, то 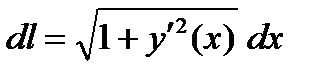 , то
, то
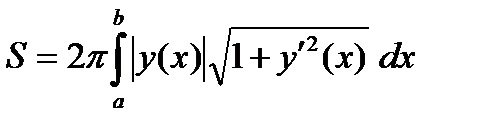 .
.
Пример. Вычислить площадь S поверхности, образованной вращением одной арки циклоиды 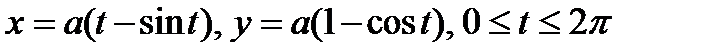 , вокруг оси OX.
, вокруг оси OX.
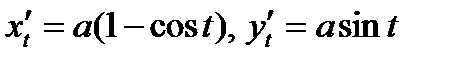
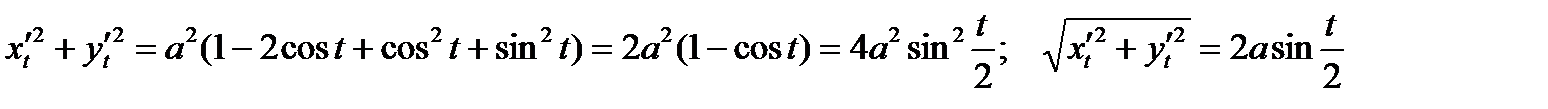
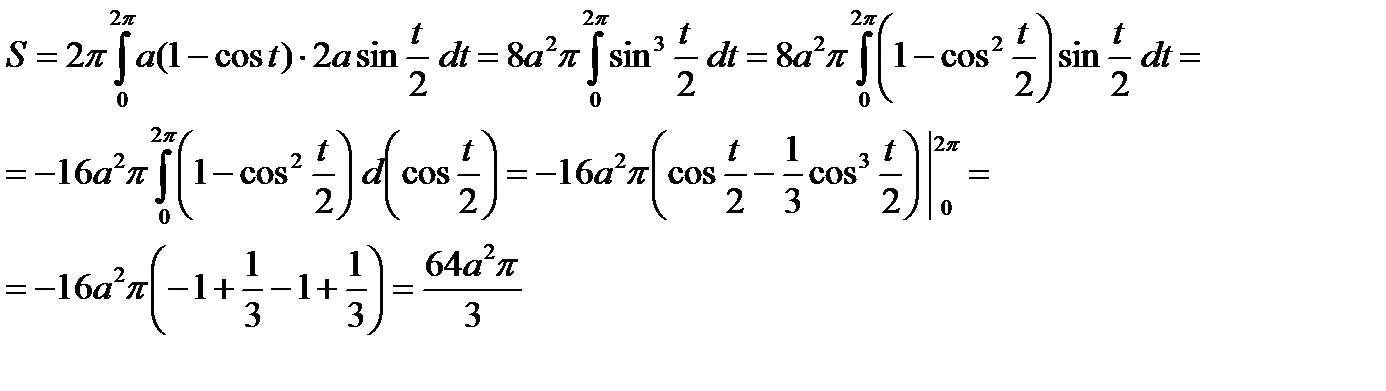
Пример. Вычислить площадь S поверхности, полученной при вращении кривой 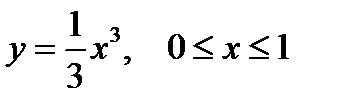 , вокруг оси OX.
, вокруг оси OX.
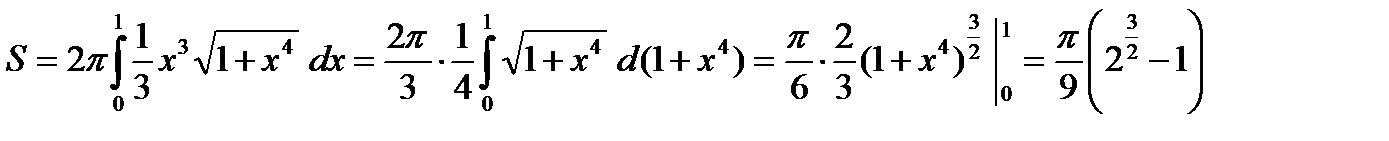
Пример. Вычислить площадь S поверхности, полученной при вращении кардиоиды 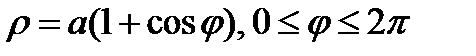 , вокруг поляры OP.
, вокруг поляры OP.
В этом случае 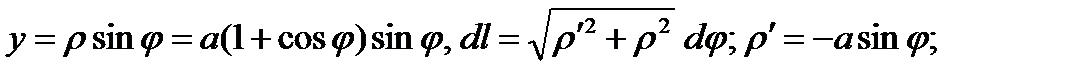
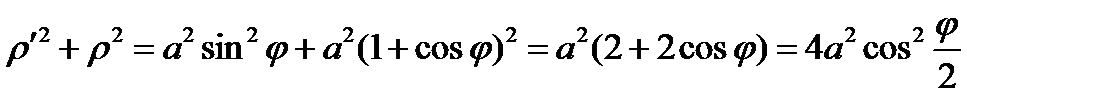

Нам достаточно взять половину кардиоиды при 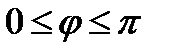 и вращать ее вокруг поляры OP.
и вращать ее вокруг поляры OP.
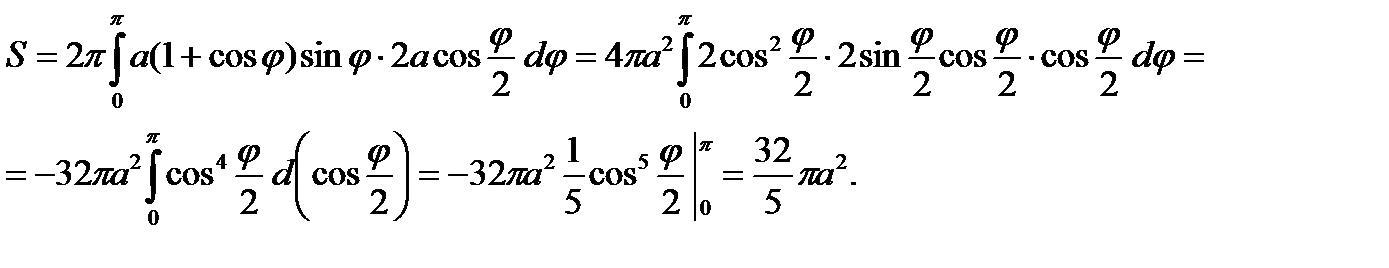
Литература:
1. Л.Д. Кудрявцев “Краткий курс математического анализа”, Москва, физматлит,2002 г., 400 с.
2. В.С. Зарубин и др. “Интегральное исчисление функций одного переменного” Москва, МГТУ им. Н.Э. Баумана, 1999 г., 528 с.
3. ”Сборник задач по математике для ВТУЗов” ред. А.В. Ефимов, Москва, физматлит, 2001 г., 485 с.
