Электромагнитные поля в проводящих средах

Эксперименты показали, что в проводящей среде электромагнитные поля распространяются медленно.

Квазистатические уравнения:

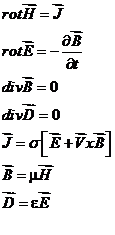
Случай неподвижных проводников.

Уравнение распространения электромагнитных волн в проводящей среде сводится к параболическим уравнениям математической физики.

Аналогично:

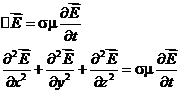
Для движущихся сред, когда

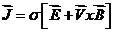
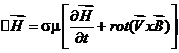
20.Магнитное число Рейнольдса

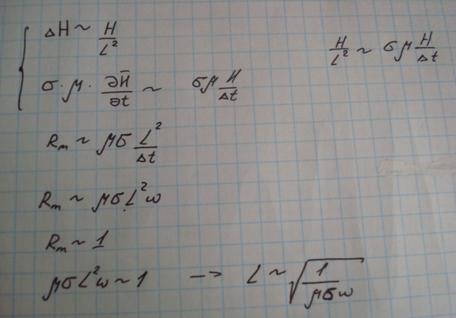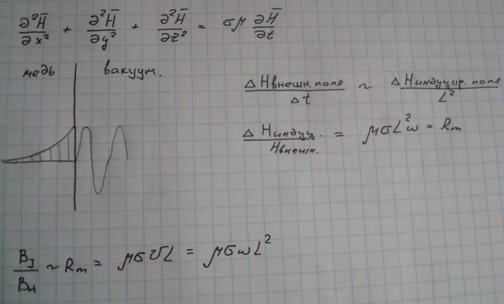Физический смысл

Магнитное число Рейнольдса-отношение индуцированных полей в проводящей среде к внешнему полю.

21.Проникновение магнитного поля в проводящую среду.

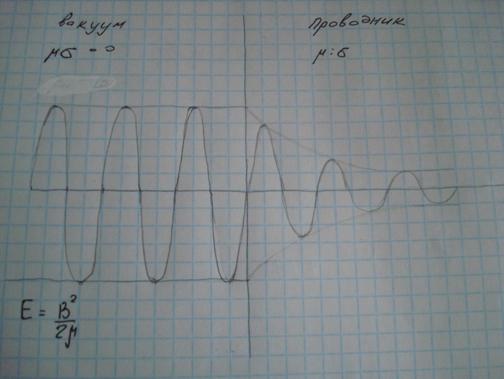
Уравнение диф.магнитного поля:

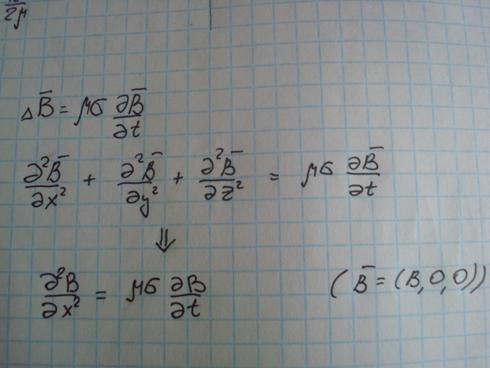
(1*)

1)Начальные условия-гармоническая волна.

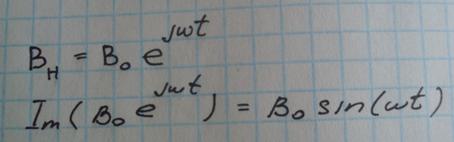2)Граничные условия:

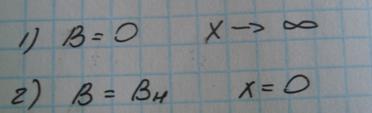3)Вид решения:

Из-за того,что волна гармоническая решение можно представить в виде (2*)

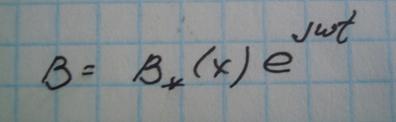4)Подставляем (2*)в (1*)

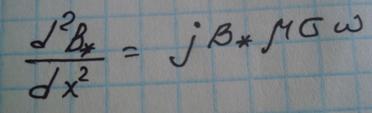
(3*)

Это ОДУ 2го порядка.

Решение:

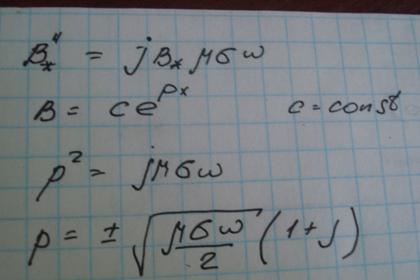(4*)

Общее решение:

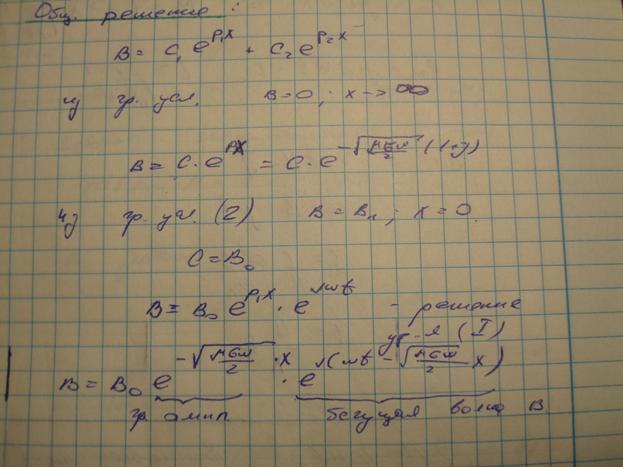
Фазовая скорость:

Глубина проникновения:

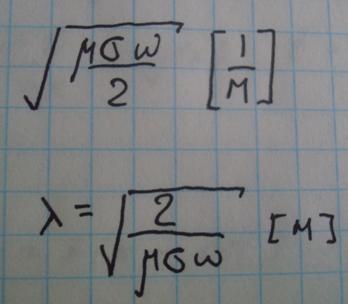
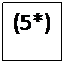Глубина проникновения-масштаб на котором поле убывает в е раз.

(5*) через магн.число Рейнольдса:

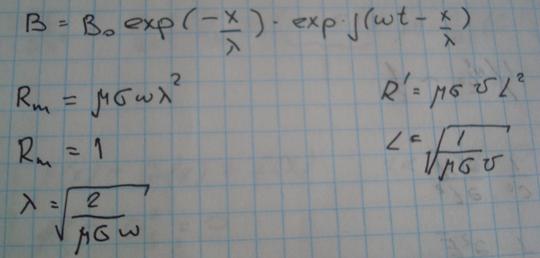
Подобие стационарных магнитных полей и температурных полей в теории теплопроводности.

Эксперименты показали, что в проводящей среде электромагнитные поля распространяются медленно.

Квазистатические уравнения:

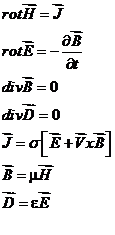
Случай неподвижных проводников.

Полученное уравнение полностью соответствует уравнению теплопроводности:

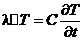
23.Электромагнитные поля в диэлектрике и вакууме.

В диэлектрике и вакууме отсутсуют токи проводимости и свободные заряды.Следовательно :

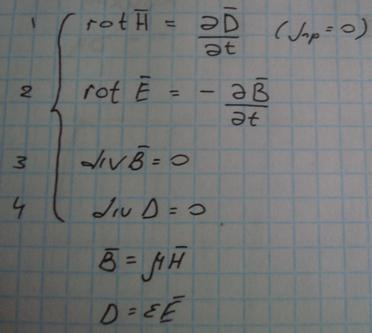
Систему уравнений можно свести к одному… относительно напряжённости.

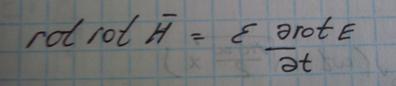
С учётом (2)

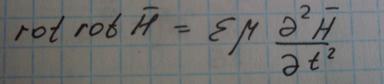
Т.о уравнения (1) и (2) было сведено к одному относительно H

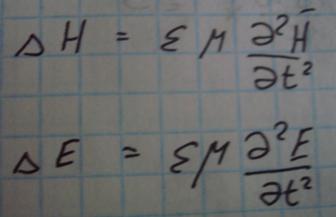
(1*)

(2*)

Уравнения (1*) и (2*) линейно зависимы т.к они получаются из одной и той же системы Максвелла.

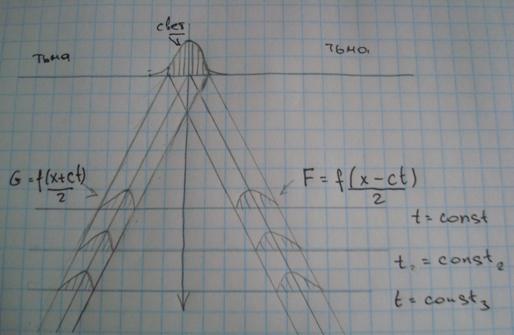
24.Распределение одномерных электромагнитных волн

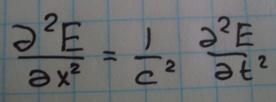Граничные условия:

Начальные условия

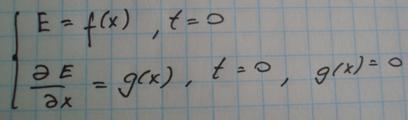
Т.Д’Аламбера:Общее решение одномерного уравнения может быть всегда представлено в виде:

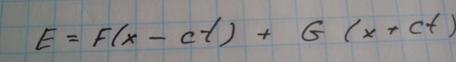F,G-любые функции.

Доказательство:

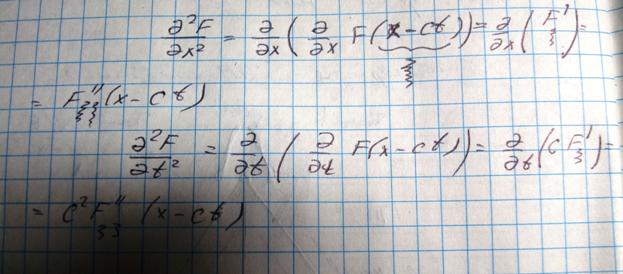
Из Н.У

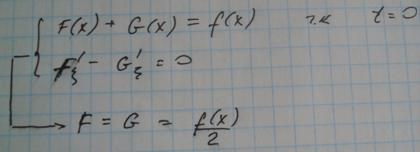
Замечание: Линии а=x-ct и b=x+ct называются характеристиками волнового уравнения .

Свойство:вдоль этих прямых ,составляющие решение Д’Аламбера(F и G) не изменяются.

Из решения Д’Аламбера можно выделить ряд областей (1*) и (2*).

(1*) характеризуется тем,что в ней световые сигналы распространяются со скоростью Vсигн>С

(2*) характеризуется тем,что в ней световые сигналы распространяются со скоростью Vсигн<С

25.Электромагнитные волны в плазме.

Поперечные волны

Для поперечных волн в бесстолкновительной плазме, температурой электронов в которой пренебрегается, диэлектрическая проницаемость имеет вид^[2]:

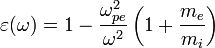
Поскольку масса ионов значительно выше, чем масса электронов, вторым слагаемым в скобках обычно можно пренебречь. Таким образом, эти волны являются аналогом электромагнитных волн в вакууме, однако отличаются от них наличием дисперсии. Дисперсионное соотношение для этих волн имеет вид^[3]:

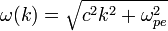
Откуда несложно определить фазовую и групповую скорости волн:

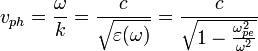
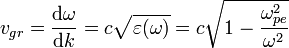
Таким образом, всегда выполняется соотношение 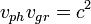. Особенностью поперечных волн в изотропной плазме является также наличие диапазона частот 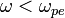, в котором диэлектрическая проницаемость отрицательна, а коэффициент преломления чисто мнимый. Волны с такой частотой не могут распространяться в плазме. При падении на слой плазмы электромагнитной волны, частота которой ниже электронной плазменной частоты, в плазме образуется скин-слой, а волна полностью отражается.

Учёт кинетических эффектов, в том числе температуры электронов (в случае нерелятивистских температур), приводит только к небольшой коррекции дисперсионного соотношения для поперечных волн, но не привносит новых свойств или эффектов. Это объясняется тем, что скорость поперечных волн значительно выше, чем скорость теплового движения электронов^[4].

Продольные волны

Продольные являются особым видом волн, характерным только для плазмы и плазмоподобных сред. Эти волны называются продольными, поскольку в них вектор электрического поля сонаправлен с волновым вектором. Характерной особенностью является также то, что наравне с колебаниями поля в ленгмюровских волнах колеблется электронная плотность. Ленгмюровские волны были впервые изучены в 1929 году И. Ленгмюром и Л. Тонксом (англ.).

Важной особенностью ленгмюроских волн является наличие у них так называемого затухания Ландау — бесстолкновительного затухания, связанного с передачей энергии волн частицам плазмы. Коэффициент затухания зависит от длины волны и в длинноволновом приближении, так что выполняется 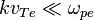(где 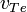— тепловая скорость электронов), равен^[5]:

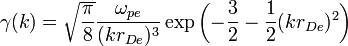
где 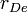— дебаевский радиус электронов.

В том же приближении дисперсионное соотношение для продольных волн имеет вид:

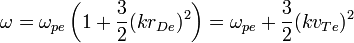
Таким образом, коротковолновые возмущения, для которых 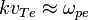, быстро затухают, поскольку для них величина частоты приближается к величине коэффициента затухания, то есть волна, фактически, перестаёт быть распространяющейся и затухает на одном периоде. При этом в той области, где волна затухает слабо, её частота практически не изменяется и приблизительно равна электронной плазменной частоте. Это позволяет говорить о том, что данная волна является просто плазменными колебаниями, распространяющимися в пространстве только за счёт наличия тепловой скорости электронов. В приближении нулевой температуры электронов скорость ленгмюровских волн точно равна нулю, а дисперсионное соотношение для них имеет вид^[:

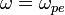
Поскольку ленгмюровские волны связаны с колебаниями электронной плотности, которые происходят на высоких частотах, движение ионов слабо сказывается на характеристиках продольных волн. Фактически, движение ионов даёт вклад только в малую поправку к плазменной частоте^[7]:

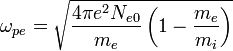
Теорема Умова-Пойнтинга.

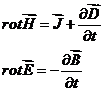
Умножим почленно первое на 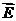, второе на 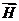и вычтем второе из первого:

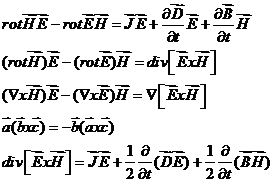
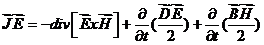- дифференциальная теорема Умова-Пойнтинга.

Проинтегрируем последнее по :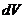

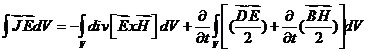
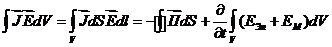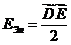, где , а ,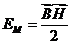

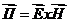- вектор Умова-Пойнтинга

Выведенные формулы 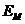и 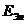верны только тогда, когда материальные уравнения линейны. В общем случае это не так.

Теорема Умова-Пойнтинга в интегральной форме утверждает – чтобы получить энергию из заданного объёма, нужно обеспечить разряд конденсаторов или индуктивных накопителей.

Теорема Умова-Пойнтинга имеет громадное научно-техническое значение, поскольку доказывает материальность ЭМП.

27 нету