Поверхностный интеграл II рода.
Пусть задана гладкая поверхность  . Сторона поверхности
. Сторона поверхности  , в каждой точки которой построен вектор нормали
, в каждой точки которой построен вектор нормали  , называется положительной, а другая ее сторона (если она существует) – отрицательной. Если, в частности, поверхность
, называется положительной, а другая ее сторона (если она существует) – отрицательной. Если, в частности, поверхность  является замкнутой и ограничивает некоторую область пространства
является замкнутой и ограничивает некоторую область пространства  , то положительной или внешней сторонойповерхности называется та ее сторона, нормальные векторы которой направлены от области
, то положительной или внешней сторонойповерхности называется та ее сторона, нормальные векторы которой направлены от области  , а отрицательной или внутренней – сторона, нормальные векторы которой направлены в область
, а отрицательной или внутренней – сторона, нормальные векторы которой направлены в область  .
.
Поверхность, у которой существует положительная (внешняя) и отрицательная (внутренняя) стороны, называется двухсторонней. Примерами двухсторонних поверхностей являются плоскость, поверхности второго порядка, тор и др. Двухсторонняя поверхность характеризуется следующим свойством: если основание вектора нормали  непрерывно перемещать по любому замкнутому контуру
непрерывно перемещать по любому замкнутому контуру  , лежащему на такой поверхности, то при возвращении в исходную точку направление
, лежащему на такой поверхности, то при возвращении в исходную точку направление  совпадает с исходным. Для односторонних поверхностей указанное перемещение нормали
совпадает с исходным. Для односторонних поверхностей указанное перемещение нормали  при возвращении в исходную точку приводит к «антинормали», т.е. к вектору
при возвращении в исходную точку приводит к «антинормали», т.е. к вектору  . Классическим примером односторонней поверхности является лист Мебиуса.
. Классическим примером односторонней поверхности является лист Мебиуса.
Поверхность  с выбранной стороной называется ориентированной.
с выбранной стороной называется ориентированной.
Пусть в прямоугольной системе координат  задана некоторая область
задана некоторая область  . И пусть в этой области задана поверхность
. И пусть в этой области задана поверхность  , ограниченная некоторой пространственной линией
, ограниченная некоторой пространственной линией  .Относительно поверхности
.Относительно поверхности  будем предполагать, что в каждой ее точке
будем предполагать, что в каждой ее точке  определяется положительное направление нормали единичным вектором
определяется положительное направление нормали единичным вектором  , направляющие косинусы которого являются непрерывными функциями координат точек поверхности.
, направляющие косинусы которого являются непрерывными функциями координат точек поверхности.
Если поверхность  задана уравнением
задана уравнением  , то нормальный вектор
, то нормальный вектор  , образующий с осью
, образующий с осью  острый угол
острый угол  , определяется следующим образом:
, определяется следующим образом:  , тогда координаты единичного вектора нормали
, тогда координаты единичного вектора нормали  :
:
 .
.
Если поверхность  задана уравнением
задана уравнением  , то
, то
 ,
,
где знак «+» берется в случае, когда угол  - острый, а знак «-» в случае, когда
- острый, а знак «-» в случае, когда  - тупой. Пусть в области
- тупой. Пусть в области 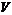 пространства
пространства  определена вектор-функция
определена вектор-функция
 ,
,
где  - функции непрерывные в области
- функции непрерывные в области 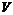 .Разобьем поверхность
.Разобьем поверхность  на элементарные площадки
на элементарные площадки  , площадки которых
, площадки которых  , а диаметры – через
, а диаметры – через  . На каждой площадке
. На каждой площадке  выберем произвольную точку
выберем произвольную точку  . Найдем интегральную сумму
. Найдем интегральную сумму  .
.
Предел интегральной суммы, найденный при условии, что  ,
,  , называется поверхностным интегралом второго рода от вектор-функции
, называется поверхностным интегралом второго рода от вектор-функции  по поверхности
по поверхности  и обозначается
и обозначается  .
.
Таким образом, по определению
 .
.
Надо отметить, что если поверхность  такова, что в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки
такова, что в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки  по поверхности, и если вектор-функция
по поверхности, и если вектор-функция  непрерывна на этой поверхности, то этот предел существует.
непрерывна на этой поверхности, то этот предел существует.
Произведение  есть проекция площадки
есть проекция площадки  на плоскость
на плоскость  , то
, то  . Аналогично получаем:
. Аналогично получаем:  ,
,  . Тогда формулу (3.3) можно записать в виде
. Тогда формулу (3.3) можно записать в виде
 . (3.4)
. (3.4)
Каждое слагаемое интегральной суммы  может быть истолковано механически следующим образом: это произведение равно объему цилиндра с основанием
может быть истолковано механически следующим образом: это произведение равно объему цилиндра с основанием  и высотой
и высотой  . Если вектор
. Если вектор  есть скорость
есть скорость
Формула Стокса
Рассмотрим в пространстве кусок двухсторонней кусочно-гладкой поверхности  , край которой образуется кусочно-гладкой кривой
, край которой образуется кусочно-гладкой кривой  . Выберем положительную сторону поверхности (из конца единичного вектора нормали
. Выберем положительную сторону поверхности (из конца единичного вектора нормали  обход границы представляется против часовой стрелки). Для циркуляции векторного поля
обход границы представляется против часовой стрелки). Для циркуляции векторного поля  вдоль контура границы имеет место формула Стокса:
вдоль контура границы имеет место формула Стокса:  , где
, где  - компоненты векторного поля,
- компоненты векторного поля,  - направляющие косинусы вектора нормали.
- направляющие косинусы вектора нормали.
Вариант №2  .
.
(4.14)
Эту же формулу Стокса можно записать и векторной форме:
 . (4.15)
. (4.15)
Формула (4.15) означает следующее: циркуляция векторного поля  вдоль замкнутого контура
вдоль замкнутого контура  равна потоку ротора этого поля через любую гладкую поверхность
равна потоку ротора этого поля через любую гладкую поверхность  , краем которой является контур
, краем которой является контур  . Направление обхода по контуру
. Направление обхода по контуру  и сторона поверхности
и сторона поверхности  одновременно или положительные, или отрицательные.
одновременно или положительные, или отрицательные.
