Механические приложения двойного интеграла.

Пусть в плоскости Oxy есть материальная пластинка, то есть некоторая область D, 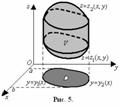по которой распределена масса с плотностью μ(x, y). Тогда:масса

пластинки

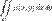.статические моменты относительно координатных осей:

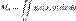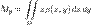, координаты (x_c, y_c) центра масс пластинки:

,

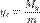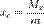
момент инерции пластинки относительно оси O_y 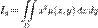относительно оси O_x 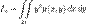относительно начала координат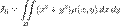

Определение и свойства тройного интеграла.

Теория тройного интеграла аналогична теории двойного интеграла.

Рассмотрим в пространстве 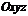замкнутую область 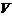. Пусть в области 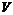задана непрерывная функция 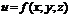.1) Разбиваем область 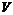на 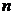«элементарных областей» 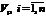.2) Объем «элементарной области» 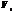обозначим , а диаметр (наибольшее расстояние между двумя точками области) – через 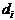.3)Возьмем произвольную точку 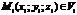.4) Находим 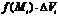.5) Составляем интегральную сумму

.

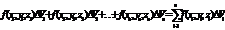6) Обозначим через 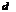длину наибольшего из диаметров «элементарных областей», т.е. 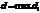, 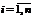. Найдем предел интегральной суммы, когда 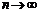так, что .

.

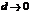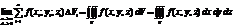Предел интегральной суммы, когда число «элементарных областей» неограниченно возрастает, а длина наибольшего диаметра стремится к нулю, называется тройным интегралом от 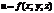на замкнутой областью 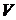.Таким образом, тройным интегралом от 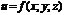по замкнутой областью 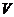называется предел интегральной суммы 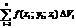, когда число «элементарных областей» неограниченно возрастает, а длина наибольшего диаметра стремится к нулю:

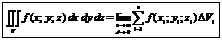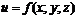. -интегрируемая функция в области ;

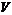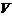-область интегрирования; 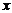, 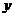и 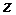-переменные интегрирования;

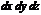или 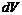-элемент объема.

Свойства

1) 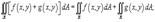2)

3) 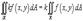, где k –

константа;

4)Если 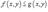в области R,то ;

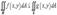5)Если 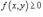в области R и 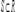, то ;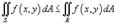

6)Если 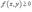на R и области R и S являются непересекающимися , то .
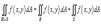Здесь означает объединение этих двух областей.

9. Вычисление тройного интеграла в декартовых координатах.Пусть функция 3-х переменных u = f (x, y, z) задана и непрерывна в замкнутой области V 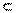xOyz. Тройной интеграл от этой функции по области V имеет вид: 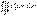, где 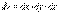.Если область V – правильная в направлении оси Oz (рис. 5), то ее можно задать системой неравенств: 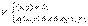где z = z1 (x, y) и z = z2 (x, y) – это уравнения поверхностей, ограничивающих область (тело) V соответственно снизу и сверху (рис. 5). Если область D можно задать системой неравенств 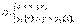то 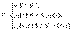В этом случае тройной интеграл от функции u = f (x, y, z) по области V можно вычислить при помощи трехкратного повторного интеграла: 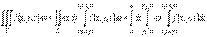.Здесь каждый внутренний интеграл вычисляется по «своей» переменной интегрирования в предположении, что переменные интегрирования внешних интегралов остаются постоянными.Существует всего 6 вариантов сведения тройного интеграла к трехкратному в декартовых координатах (в зависимости от выбранного порядка интегрирования).Вычисление тройного интеграла в цилиндрических координатахЦилиндрические координаты точки М в пространстве – это ее полярные координаты на плоскости xOy и координата z, т.е. 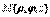.Преобразование тройного интеграла по области V к цилиндрическим координатам осуществляется при помощи формул 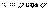, , 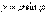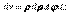: 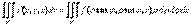.Если область V задана системой неравенств: 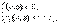причем 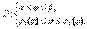то V: 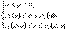Вычисление тройного интеграла по области V в цилиндрических координатах сводится к вычислению трехкратного интеграла в соответствии с записанной системой неравенств для области V: .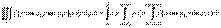