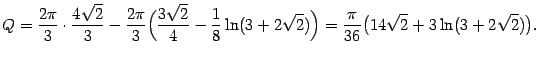Нахождение объёма тела по площадям поперечных сечений

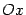Пусть в пространстве задано тело. Пусть построены его сечения плоскостями, перпендикулярными оси и проходящими через точки x 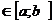на ней. Площадь фигуры, образующейся в сечении, зависит от точки х, определяющей плоскость сечения. Пусть эта зависимость известна и задана непрерывной на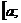 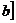функцией 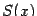. Тогда объем части тела, находящейся между плоскостями х=а и х=в вычисляется по формуле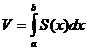

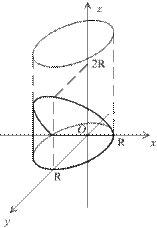
Пример. Найдём объём ограниченного тела, заключённого между поверхностью цилиндра радиуса 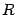: 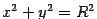, горизонтальной плоскостью 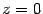и наклонной плоскостью z=2y и лежащего выше горизонтальной плоскости .

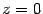Очевидно, что рассматриваемое тело 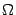проектируется на ось 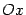в отрезок 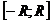, а при x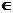 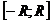поперечное сечение тела представляет собою прямоугольный треугольник с катетами y и z=2y, где y можно выразить через x из уравнения цилиндра:

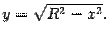
Поэтому площадь S(x) поперечного сечения такова:

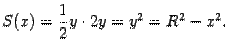
Применяя формулу, находим объём тела :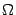

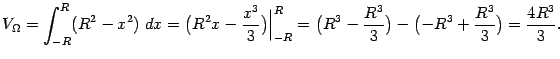
Вычисление объемов тел вращения

Пусть на отрезке[a, b] задана непрерывная знакопостоянная функция y=f(x). Объемы тела вращения, образованного вращением вокруг оси Ох (или оси Оу) криволинейной трапеции, ограниченной кривой y=f(x) (f(x) 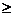0) и прямыми у=0, х=а, х=b, вычисляются соответственно по формулам:

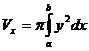, (19)

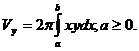(20)

Если тело образуется при вращении вокруг оси Оу криволинейной трапеции, ограниченной кривой и прямыми x=0, y=c, y=d, то объем тела вращения равен

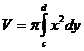. (21)

Пример. Вычислить объем тела, полученного вращением фигуры, ограниченной линиями 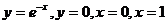вокруг оси Ох.

По формуле (19) искомый объем

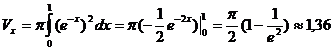(ед.²)

Пример. Пусть в плоскости xOy рассматривается линия y=cosx на отрезке .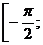

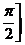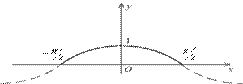Эта линия вращается в пространстве вокруг оси 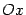, и полученная поверхность вращения ограничивает некоторое тело вращения (см. рис.). Найдём объём 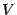этого тела вращения.

Согласно формуле, получаем:

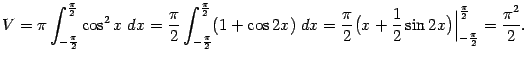
Площадь поверхности вращения

Если дуга кривой, заданная неотрицательной функцией 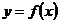, , 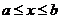вращается вокруг оси Ox, то площадь поверхности вращения вычисляется по формуле 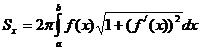, где a и b — абсциссы начала и конца дуги.

Если дуга кривой, заданная неотрицательной функцией 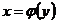, , 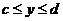вращается вокруг оси Oy, то площадь поверхности вращения вычисляется по формуле

,

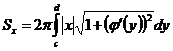где с и d — абсциссы начала и конца дуги.

Если дуга кривой задана параметрическими уравнениями 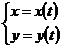, , 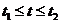причем 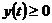, то

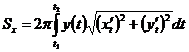
Если дуга задана в полярных координатах 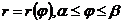, то

.

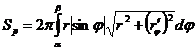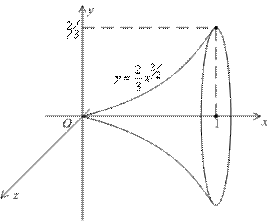
Пример. Вычислим площадь поверхности, образованной вращением в пространстве вокруг оси 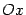части линии y= 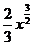, расположенной над отрезком 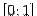оси .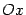

Так как 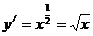, то формула даёт нам интеграл

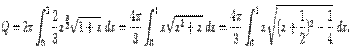
Сделаем в последнем интеграле замену t=x+(1/2) и получим:

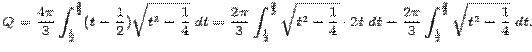
В первом из интегралов правой части сделаем замену z=t²- :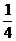

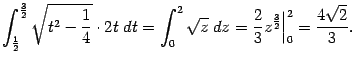
Для вычисления второго из интегралов в правой части обозначим его 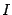и проинтегрируем по частям, получив уравнение для :

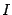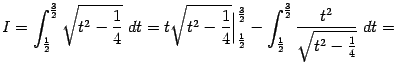
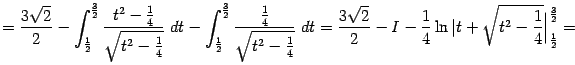
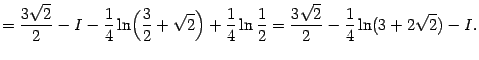
Перенося 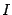в левую часть и деля на 2, получаем

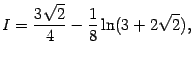
откуда, наконец,