Движения по кривой интегрирования.

Пусть кривая L представляет собой некоторую линию, соединяющую точки А и В. Ясно, что L может быть пройдена двояко: от А до В или от В до А.

Слагаемые интегральной суммы в (3) 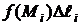не меняют знак при изменении направления движения по кривой интегрирования, так как длина − величина всегда положительная.

Слагаемые интегральной суммы (7) меняют знак при изменении направления движения по кривой интегрирования, так как приращения независимых переменных изменяют знак при этом.

Следовательно,

− для интегралов первого рода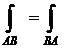

− для интегралов второго рода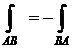

Чтобы внести определенность относительно знака интеграла второго рода по замкнутому контуру (его иногда обозначают символом 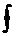), условились из двух возможных направлений обхода контура положительным называть тот, при котором область, лежащая внутри этого контура, остается слева по отношению к точке, совершающей обход.

п. 20. 2. Вычисление криволинейных интегралов I − рода.

1) Кривая интегрирования L задана в декартовых координатах х, у системой параметрических уравнений:

x = x (t), y = y (t), z = z (t) при t Î [a, b].

В этом случае криволинейный интеграл первого рода сводится к определенному интегралу по формуле

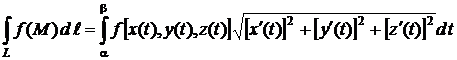(1)

Пример. Вычислить 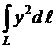, где L − окружность x² + y² = R².

Решение. L: x = R cos t, y = R sin t при t Î [0, 2p]. По формуле (1) получим

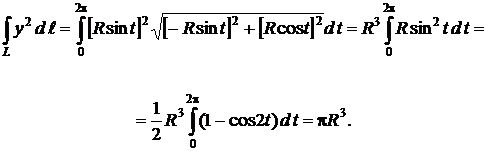
2) Кривая интегрирования L задана в декартовых координатах х, у системой уравнений:

y = y (х), z = z (х) при х Î [а, b].

Такой способ задания кривой можно рассматривать как параметрический х = х, y = y (х), z = z (х) с параметром х при х Î [а, b]. Согласно этому, сделав замену в (1), получим формулу сведения криволинейного интеграла первого рода к определенному интегралу

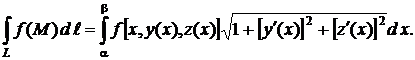(2)

Пример. Вычислить 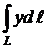, где L: 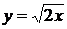при х Î [0, 4].

Решение. По формуле (2) получим

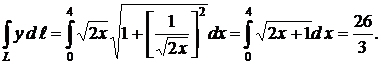
п. 20. 3. Вычисление криволинейных интегралов II − рода.

1) Кривая интегрирования L задана в декартовых координатах х, у системой параметрических уравнений:

x = x (t), y = y (t), z = z (t) при t Î [a, b].

В этом случае криволинейный интеграл второго рода сводится к определенному интегралу по формуле

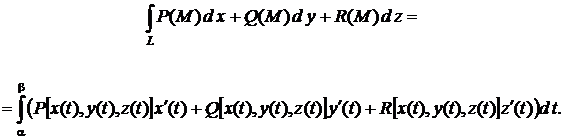(3)

Пример. Вычислить 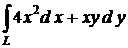, где L − верхняя полвина окружности x² + y² = R², проходимая от точки (R, 0) до точки (− R, 0).

Решение. L: x = R cos t, y = R sin t при t Î [0, p]. По формуле (3) получим

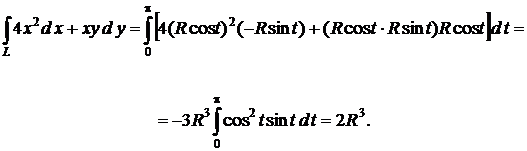
2) Кривая интегрирования L задана в декартовых координатах х, у системой уравнений:

y = y (х), z = z (х) при х Î [а, b].

Такой способ задания кривой можно рассматривать как параметрический х = х, y = y (х), z = z (х) с параметром х при х Î [а, b]. Согласно этому, сделав замену в (3), получим формулу сведения криволинейного интеграла второго рода к определенному интегралу

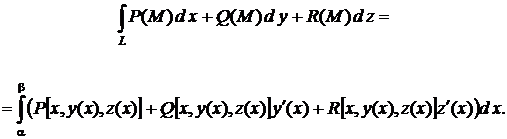(4)

Пример. Вычислить 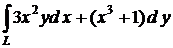, где L − парабола x² = y, проходимая от точки (0, 0) до точки (1, 1).

Решение. По формуле (4) получим

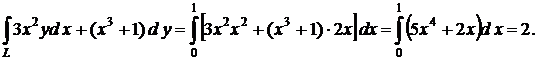
Теорема. Для криволинейных интегралов обоих родов: если точка С делит кривую интегрирования АВ на две части АС и СВ, то

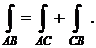(5)

Следствие. Если отрезки кривых АСВ и ВDA составляют замкнутый контур L (L = ACB È BDA), то для интеграла второго рода

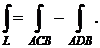(6)

П. 20.4. Формула Грина.

Определение. Замкнутая область называется простой, если ее граница пересекается с прямыми, параллельными декартовым осям координат, не более чем в двух точках.

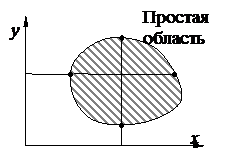Рис. 1 Рис. 2

Теорема 1. Если G − простая область, ограниченная контуром L, и P (x, y), Q (x, y) − непрерывные с непрерывными частными производными функции в G, включая точки М Î L, то справедливо равенство

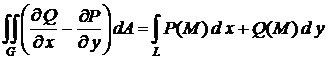. (1)

называемое формулой Грина.

Определение.Плоская область G называется односвязной, если любой замкнутый контур L, целиком лежащий в G, ограничивает область, целиком принадлежащую области G.

Образно говоря, в односвязной области нет «дыр».

Теорема 2. Площадь А односвязной области G (рис. 1), ограниченной замкнутым контуром L, в декартовых координатах х и у определяется формулой

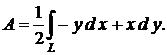(2)