Вычисление Поверхностных интегралов второго рода (ПИ-2)
Рассмотрим ПИ-2  n0)dq, где ā=(X(x;y;z),Y(x;y;z),Z(x;y;z)) , n0= (
n0)dq, где ā=(X(x;y;z),Y(x;y;z),Z(x;y;z)) , n0= (  ).
).
Если прямые || осям координат пересекают поверхность Q не более чем в одной точке,то (ā;n0)=Xcosα+Ycosβ+Zcosγи ПИ-2 принимает вид:  (**) Выражение (**) назыв. Скалярной формой ПИ-2. Полученное представление позволяет рассматривать ИП-2 как сис-му трех ПИ-1.Заметим,что для вычисления ПИ-2 cosγdq есть проекция dq на плоскость XOY, взятая со знаком «+» или «–». «–» соответствует тупому углу между
(**) Выражение (**) назыв. Скалярной формой ПИ-2. Полученное представление позволяет рассматривать ИП-2 как сис-му трех ПИ-1.Заметим,что для вычисления ПИ-2 cosγdq есть проекция dq на плоскость XOY, взятая со знаком «+» или «–». «–» соответствует тупому углу между  и OZ Т.о.
и OZ Т.о.  dq =
dq =  )dq=
)dq=  (***) где y=y1(x;z),… получены из уравнения поверхности Q в рез-те выражения переменных x,y и z.Qxy,Qyz,Qxz – проекции поверхности Q на плоскость XOY,YOZ и XOZ соответственно.
(***) где y=y1(x;z),… получены из уравнения поверхности Q в рез-те выражения переменных x,y и z.Qxy,Qyz,Qxz – проекции поверхности Q на плоскость XOY,YOZ и XOZ соответственно.
Знак «-» перед интегралом выбирается в случае если вектор нормалью к поверхности образует с соответственной осью тупой угол. Пример: Вычислить поверхностный интеграл  )dq , где ā(0;0;x2y2z);Q – внутренняя сторона нижней половины сферы Q=x2+y2+zz2=R2,где z
)dq , где ā(0;0;x2y2z);Q – внутренняя сторона нижней половины сферы Q=x2+y2+zz2=R2,где z 
 + 0dxdz + x2y2 zdxdy = -
+ 0dxdz + x2y2 zdxdy = -  x2y2 zdxdy = -
x2y2 zdxdy = -  x2y2
x2y2  dxdy= [x=pcosϒ;y=psinϒ]= -
dxdy= [x=pcosϒ;y=psinϒ]= -  dpdϒ=-
dpdϒ=-  dpdϒ=-
dpdϒ=-  =…
=…
Векторные поля
Определение 1: Векторным полем называется пространство Rn или его часть,в каждом точке j-го определена векторная функция ā=ā(p)
Определение 2:Векторной линией(силовой) векторного поляā=ā(р) называется линия,в каждой точке Pj-й вектор ā(р) направлен по касательной.
Определение 3:Пусть ā=ā(р) – векторное поле R3 .Векторной трубкой называется поверхность,образованная векторными линиями,проходящ.из точки некоторой замкнутой кривой L,не совпадающей ни с одной из векторных линий.
Определение 4:Потоком вектора ā,через поверхность S называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности, т.е. П= 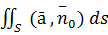
Физический смысл потока: он равен количеству жидкости,протекающей за единицу времени через данную поверхность.
Определение 5:Дивергенцией векторного поля ā(р)(расходимостью) наз.число обознач div āp(p) и равное lim-у отношения потока поля ā(р) из замкнутой поверхности Q к величине объема ∆V,огранич.данной поверхностью,когда ∆V 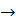 0,т.е. при условии что ∆Q стягивается в т.Р
0,т.е. при условии что ∆Q стягивается в т.Р
div ā(p)= 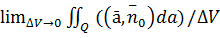
т.о.divā(p) характеризует мощность наход.в точке Р источника,если divā(p)<0,и стока div ā(p)>0.
Если же div ā(p)=0,то в т.Р нет источников и стоков.
Свойства дивергенции:
1. Если ā – постоянный вектор, то div ā= 0.
2. div(c⋅ā) = с⋅divā, где с = const.
3. div (ā + b) = divā + divb т.е. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.
4. Если U – скалярная функция, ā – вектор, то div (U⋅ā) = U⋅divā + āgradU.
Док-во (4 св-во):
divUā= 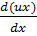 +
+ 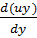 +
+ 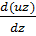 =
= 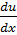 *x
*x 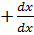 *u+
*u+ 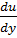 *y+
*y+ 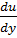 *u+
*u+ 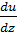 *z+
*z+ 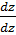 *u=
*u=
u( 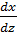 +
+ 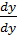 +
+ 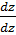 )(x;y;z)*(
)(x;y;z)*( 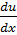 ;
; 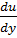 ;
; 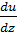 )=u*div ā+ā*grad u.
)=u*div ā+ā*grad u.
Теорема Остроградского-Гаусса:
Если векторная функция ā(р) непрерывно диф-ма в области V,огранич.замкнутой поверхностью Q,то поток векторного поля ā(р) из Q в направлении внешней нормали 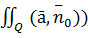 da0=
da0= 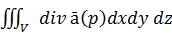
Формула Остроградского-Гаусса означает, что поток векторного поля через
замкнутую поверхность S (в направлении внешней нормали, т.е. изнутри) равен
тройному интегралу от дивергенции этого поля по объему V, ограниченному
данной поверхностью.
