Общие теоремы динамики системы. Теорема об изменении количества движения материальной точки и системы. Закон сохранения количества движения в системе.

1. Количество движения замкнутой системы с течением времени не изменяется:

dK/dt = 0 или K= SKi = Smivi = const

Это один из основных законов природы, вытекающий из однородности пространства.

2. Закон сохранения количества движения показывает, что взаимодействие тел, составляющих замкнутую систему, приводит только к обмену количествами движения между этими телами, но не может изменить движения системы как целого: при любом взаимодействии между телами, образующими замкнутую систему, скорость движения центра инерции этой системы не изменяется, т. е.
dvc/dt = 0

где vc — скорость центра инерции.

11. Теорема импульсов для материальной точки и системы

Теорема об изменении момента количества движения. Закон сохранения главного момента количества движения системы.

Применение теоремы моментов к твёрдому телу, вращающемуся вокруг неподвижной оси.

Понятия о моментах инерции твёрдого тела. Момент инерции твёрдого тела, вращающегося вокруг неподвижной оси. Теорема Штейнера-Гюйгенса.

Элементарная и полная работа силы. Мощность. Работа внутренних сил. Работа равнодействующей силы.

Элементарная работа силы равна произведению элементарного перемещения на проекцию силы на это перемещение.

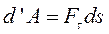Элементарная работа силы равна скалярному произведению элементарного импульса на скорость точки её приложения.

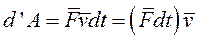Полную работу силы 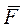на перемещении точки из положения 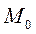в положение 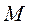определяют как предел суммы её элементарных работ, т.е.

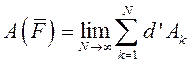
Если же сила является функцией времени (переменная сила) то работа силы на промежутке времени от 0 до t, соответствующем точкам 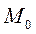и 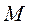, определяется выражением

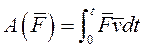
Работа силы зависит от характера движения точки приложения силы. Так, А = 0, если сила приложена к неподвижной точке или к точке, скорость которой во время движения равна нулю (например, МЦС)

Работа равнодействующей силы.

Рассмотрим систему сил, приложенную к рассматриваемой точке. Эта система имеет равнодействующую 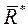, причём

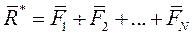
Тогда работа силы 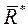на перемещении точки из 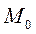в текущее положение М равна алгебраической сумме работ составляющих сил на том же перемещении:

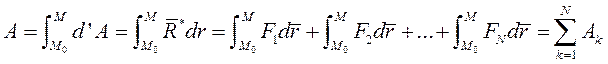
Мощность.

Отношение элементарной работы силы к промежутку времени, за которое оно произошло, называется мощностью.

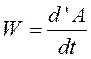
Так как 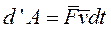то

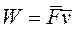
Мощность силы равна скалярному произведению силы на скорость точки её приложения.

Если нагруженное тело находится в равновесии, то внутренние силы равны по значению внешним силам и противоположны им по направлению. Очевидно, что они препятствуют развитию деформации. Работа внутренних сил (U), с учетом их направления по отношению к деформации, всегда является отрицательной.

Работа внешних сил равна взятой с обратным знаком работе внутренних сил:

.
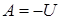