Законы классической механики. Дифференциальное уравнение движения материальной точки.

Законы классической механики. Дифференциальное уравнение движения материальной точки.

Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения.

В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению

ΣX = m(d²x/dt²); ΣY = m(d²y/dt²),

где ΣX и ΣY – алгебраические суммы проекций сил, действующих на точку, на соответствующие координатные оси; x и y – текущие координаты точки.

С помощью полученных дифференциальных зависимостей решаются две основные задачи динамики:

• по заданному движению точки определяют действующие на нее силы;
• зная действующие на точку силы, определяют ее движение.

Свободные колебания материальной точки. Влияние постоянной силы на свободное колебание

Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии (потенциальной или кинетической) при отсутствии внешних воздействий

Дифференциальное уравнение свободных колебаний при отсутствии сопротивления:

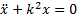
Общее решение этого уравнения имеет вид 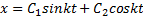, где

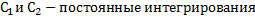
В случае, когда действующая на материальную точку позиционная сила стремиться вернуть ее в исходное положение, движение точки будет носить колебательный характер. Такую силу принято называть восстанавливающей.

Под действием восстанавливающей силы материальная точка совершает движение по синусоидальному закону, т.е. гармоническое колебательное движение.

Постоянная сила Р не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силы F, а только смещает центр этих колебаний в сторону действия силы Р на величину ста­тического отклонения .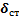

Движение материальной точки в условиях резонанса

В случае, когда 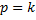, т.е. когда частота возмущающей силы равна частоте собственных колебаний, имеет место так называемое явление резонанса.

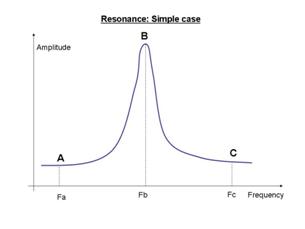
Резонанс - это резкое возрастание амплитуды вынужденных колебаний. Возникает, когда частота собственных колебаний совпадает с частотой вынуждающей силы

Размахи вынужденных колебаний при резонансе будут со временем неограниченно возрастать

Вынужденные колебания материальной точки при сопротивление пропорциональном скорости.

Вращательное движение

В этом случае 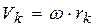. Тогда

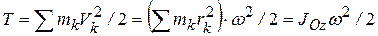
– кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости.

Теоре́ма Кёнига

Кинетическая энергия механической системы есть энергия движения центра масс плюс энергия движения относительно центра масс:

T=T0+Tr{\displaystyle {T\;=\;T_{0}+T_{r}}\;,}

Где T - {\displaystyle T} TTTTTTtTTTTtt полная кинетическая энергия системы, {\displaystyle T_{0}}T0 — кинетическая энергия движения центра масс, {\displaystyle T_{r}}Tr — относительная кинетическая энергия системы^[2].

Иными словами, полная кинетическая энергия тела или системы тел в сложном движении равна сумме энергии системы в поступательном движении и энергии системы в её сферическом движении относительно центра масс.

Более точная формулировка: полная кинетическая энергия всей системы равна сумме кинетической энергии всей массы системы, сосредоточенной в ее центре масс и движущейся со скоростью центра масс плюс кинетическая энергия той же системы в ее относительной системе относительно центра масс

Рисунок 1 - Свободное падение тела.

Так как груз малыми размерами то сопротивление воздуха достаточно мало и энергия на его преодоление мала и ею можно пренебречь. Скорость движения тела не высока и на малом расстоянии не достигает момента, когда она уравновешивается трением о воздух и ускорение прекращается.

В момент столкновения с землей кинетическая энергия максимальна. Так как тело обладает максимальной для него скоростью. А потенциальная энергия равна нулю, так как тело достигло поверхности земли и высота равна нулю. То есть что происходит, максимальная потенциальная энергия в верхней точке, по мере движения переходит в кинетическую, которая в свою очередь достигает максимума в нижней точке. Но сумма всех энергий в системе за время движения остается постоянной. Насколько уменьшилась потенциальная энергия, настолько увеличилась кинетическая.

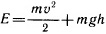
Идеальные связи

При движении точки по поверхности или по кривой реакция связи может быть разложена на нормальную и касательную составляющие. Касательная составляющая реакции представляет собой силу трения. Чем более гладкой будет поверхность или кривая, тем меньше будет касательная составляющая реакции. Если поверхность или кривая абсолютно гладкие, то реакция нормальна к поверхности

Идеальными связяминазываются связи без трения, реакции которых не имеют касательных составляющих

Принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.

Реакция связиСила, с которой данная связь действует на тело, препятствующая тем или иным его перемещениям, называется реакцией связи. Реакция связинаправлена в сторону противоположную той, куда связь не дает перемещаться телу.

Жесткая заделка

Нахождение реакции жесткой заделки сводится к определению составляющих Х_А и Y_A препятствующих линейному перемещению балки в плоскости действия сил, и алгебраической величине момента m_A, препятствующего вращению балки под действием приложенных к ней сил.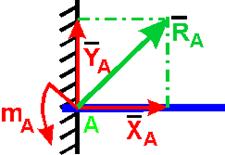

Рис.4

Решение.Эту задачу можно решить известными методами статики, составляя уравнения равновесия. Но при этом придется прежде отыскать усилия в стержнях. Принцип возможных перемещений позволяет найти силу F проще, с помощью общего уравнения статики.

Показываем активные силы и 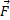. Даем системе возможное перемещение, повернув стержень АО на угол 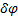(рис.66). Так как желоб совершит поступательное движение, то перемещения всех его точек будут одинаковы:

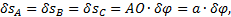
где a=AO=BD.

Составляем уравнение работ: 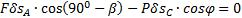. Угол .

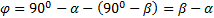Поэтому получим 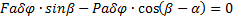. Отсюда .

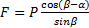Общее уравнение динамики.

По принципу Даламбера материальную систему, движущуюся под действием некоторых сил, можно рассматривать находящейся в равновесии, если ко всем точкам системы приложить их силы инерции. Значит можно воспользоваться и принципом возможных перемещений.

В уравнение работ (1) добавится еще сумма работ сил инерции точек на их возможных перемещениях:

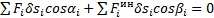. (3)

Или по принципу возможных скоростей (2):

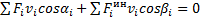(4)

Эти уравнения называют общим уравнением динамики. Оно позволяет решать большой класс задач на исследование движения довольно сложных материальных систем.

Уравнения (3) и (4) показывают, что в любой фиксированный момент времени сумма элементарных работ активных сил и сил инерции на любых виртуальных перемещениях равна нулю при условии, что на систему наложены идеальные и удерживающие связи.

Стоит подчеркнуть еще одно важное достоинство этого метода, общего уравнения динамики, – реакции связей (идеальных) исключаются при исследовании движения системы.

Иногда это уравнение можно использовать для исследования движения механических систем и в тех случаях, когда не все связи являются идеальными, например, когда имеются связи с трением. Для этого следует к активным силам добавить те составляющие реакций, которые обусловлены наличием сил трения.

Рис.11

Равновесие считается устойчивым, если телу в этом положении сообщить малую скорость или сместить на малое расстояние и эти отклонения в дальнейшем не увеличатся.

Можно доказать (теорема Лагранжа-Дирихле), что если в положении равновесия консервативной системы ее потенциальная энергия имеет минимум, то это положение равновесия устойчиво.

Для консервативной системы с одной степенью свободы условие минимума потенциальной энергии, а значит и устойчивости положения равновесия, определяется, второй производной, ее значением в положении равновесия,

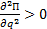. (11)

Законы классической механики. Дифференциальное уравнение движения материальной точки.

Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения.

В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.

Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению

ΣX = m(d²x/dt²); ΣY = m(d²y/dt²),

где ΣX и ΣY – алгебраические суммы проекций сил, действующих на точку, на соответствующие координатные оси; x и y – текущие координаты точки.

С помощью полученных дифференциальных зависимостей решаются две основные задачи динамики:

• по заданному движению точки определяют действующие на нее силы;
• зная действующие на точку силы, определяют ее движение.