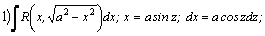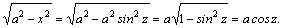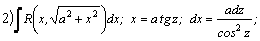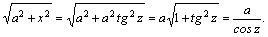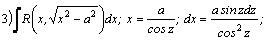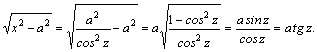Интегрирование простейших дробей.
Задача нахождения неопределенного интеграла дробно рациональной функции сводится к интегрированию простейших дробей. Поэтому рекомендуем для начала ознакомиться с разделом теории разложение дроби на простейшие.
Пример.
Найти неопределенный интеграл  .
.
Решение.
Так как степень числителя подынтегральной функции равна степени знаменателя, то для начала выделяем целую часть, проводя деление столбиком многочлена на многочлен:
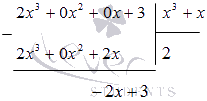
Поэтому, 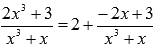 .
.
Разложение полученной правильной рациональной дроби 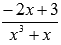 на простейшие дроби имеет вид
на простейшие дроби имеет вид 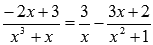 . Следовательно,
. Следовательно,
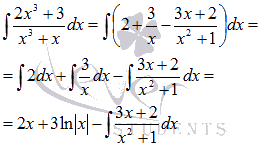
Полученный интеграл представляет собой интеграл простейшей дроби третьего типа. Забегая немного вперед, отметим, что взять его можно методом подведения под знак дифференциала.
Так как 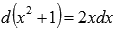 , то
, то 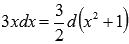 . Поэтому
. Поэтому
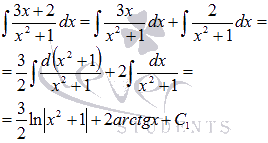
Следовательно,
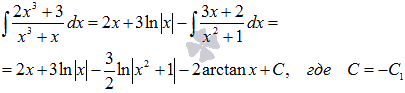
Теперь перейдем к описанию методов интегрирования простейших дробей каждого из четырех типов.
Интегрирование простейших дробей первого типа 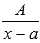
Для решения этой задачи идеально подходит метод непосредственного интегрирования:
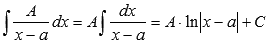
Пример.
Найти множество первообразных функции 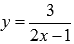
Решение.
Найдем неопределенный интеграл 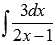 , используя свойства первообразной, таблицу первообразных и правило интегрирования
, используя свойства первообразной, таблицу первообразных и правило интегрирования 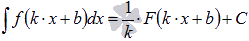 .
.
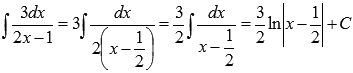
К началу страницы
Интегрирование простейших дробей второго типа 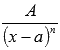
Для решения этой задачи также подходит метод непосредственного интегрирования:
Пример.
Найдите неопределенный интеграл 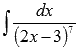 .
.
Решение.
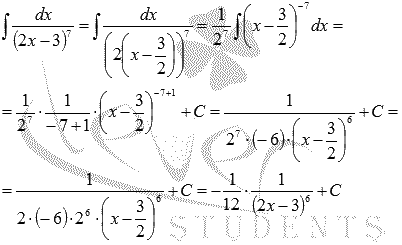
К началу страницы
Интегрирование простейших дробей третьего типа 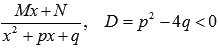
Для начала представляем неопределенный интеграл 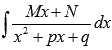 в виде суммы:
в виде суммы:
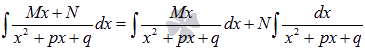
Первый интеграл берем методом подведения под знак дифференциала:
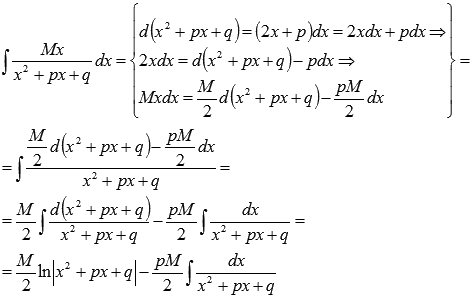
Поэтому,
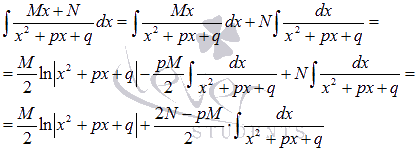
У полученного интеграла 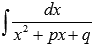 преобразуем знаменатель:
преобразуем знаменатель:
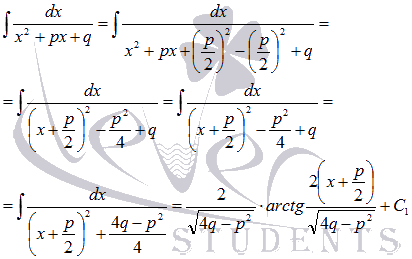
Следовательно,
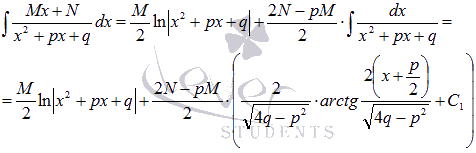
Формула интегрирования простейших дробей третьего типа принимает вид:
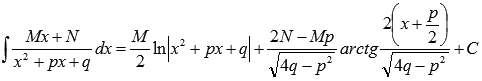
Пример.
Найдите неопределенный интеграл 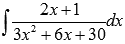 .
.
Решение.
Используем полученную формулу:
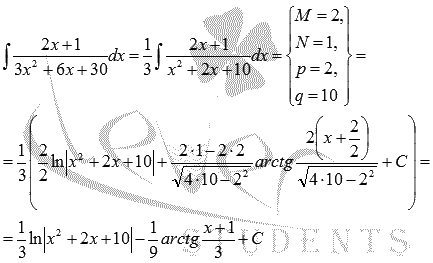
Если бы у нас не было этой формулы, то как бы мы поступили:
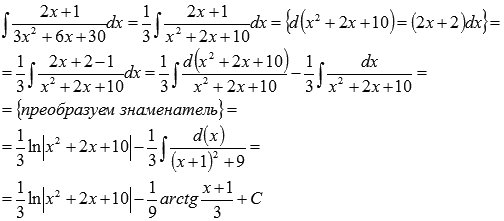
К началу страницы
Интегрирование простейших дробей четвертого типа 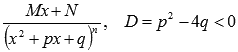
Первый шаг – подводим под знак дифференциала:
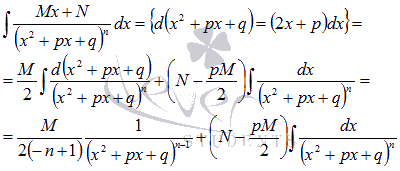
Второй шаг – нахождение интеграла вида 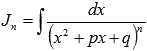 . Интегралы подобного вида находятся с использованием рекуррентных формул. (Смотрите раздел интегрирование с использованием рекуррентных формул). Для нашего случая подходит следующая рекуррентная формула:
. Интегралы подобного вида находятся с использованием рекуррентных формул. (Смотрите раздел интегрирование с использованием рекуррентных формул). Для нашего случая подходит следующая рекуррентная формула:
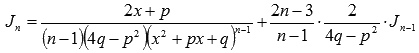
Пример.
Найдите неопределенный интеграл 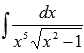
Решение.
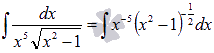
Для данного вида подынтегральной функции используем метод подстановки. Введем новую переменную (смотрите раздел интегрирование иррациональных функций):
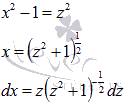
После подстановки имеем:
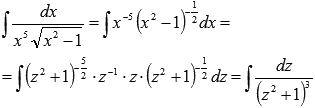
Пришли к нахождению интеграла дроби четвертого типа. В нашем случае имеем коэффициенты М = 0, р = 0, q = 1, N = 1 и n = 3. Применяем рекуррентную формулу:
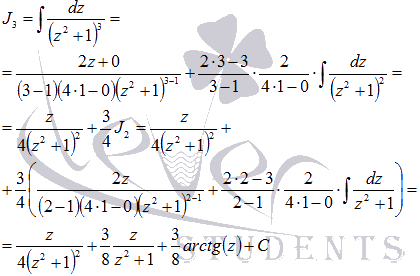
После обратной замены 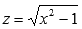 получаем результат:
получаем результат:
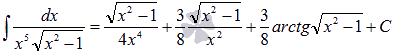
| Интегрирование тригонометрических функций | ||||||||||||||||||||
1.Интегралы вида 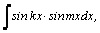 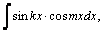 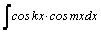 вычисляются преобразованием произведения тригонометрических функций в сумму по формулам: вычисляются преобразованием произведения тригонометрических функций в сумму по формулам: 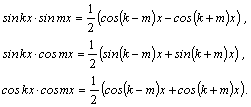 Например, Например, 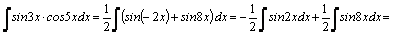 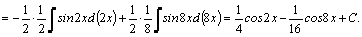 2.Интегралы вида 2.Интегралы вида 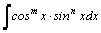 , где m или n– нечетное положительное число, вычисляются подведением под знак дифференциала. Например, , где m или n– нечетное положительное число, вычисляются подведением под знак дифференциала. Например,  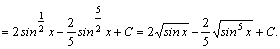 3.Интегралы вида 3.Интегралы вида 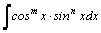 , где m и n–четные положительные числа, вычисляются с помощью формул понижения степени: , где m и n–четные положительные числа, вычисляются с помощью формул понижения степени: 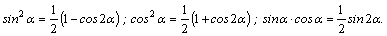 Например, Например, 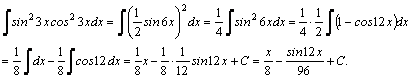 4.Интегралы 4.Интегралы 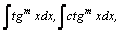 где где 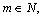 вычисляются заменой переменной: вычисляются заменой переменной: 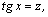 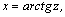 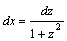 или или 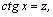 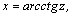 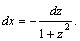 Например, Например, 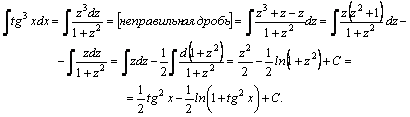 5.Интегралы вида 5.Интегралы вида 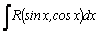 сводятся к интегралам от рациональных дробей с помощью универсальной тригонометрической подстановки сводятся к интегралам от рациональных дробей с помощью универсальной тригонометрической подстановки 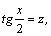 тогда тогда 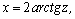 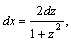 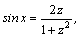 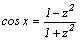 (т.к. (т.к. 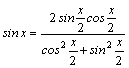 =[после деления числителя и знаменателя на =[после деления числителя и знаменателя на 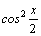 ]= ]= 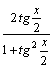 ; ; 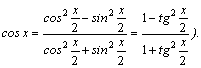 Например, Например, 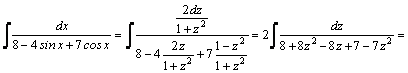 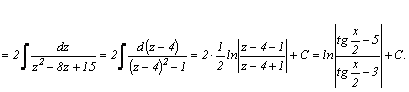 Следует заметить, что использование универсальной подстановки нередко приводит к громоздким выкладкам. Следует заметить, что использование универсальной подстановки нередко приводит к громоздким выкладкам. | ||||||||||||||||||||
| §5. Интегрирование простейших иррациональностей | ||||||||||||||||||||
Рассмотрим методы интегрирования простейших видов иррациональностей. 1.  Функции такого вида интегрируются так же, как простейшие рациональные дроби 3–го типа: в знаменателе из квадратного трехчлена выделяется полный квадрат и вводится новая переменная. Пример. Функции такого вида интегрируются так же, как простейшие рациональные дроби 3–го типа: в знаменателе из квадратного трехчлена выделяется полный квадрат и вводится новая переменная. Пример. 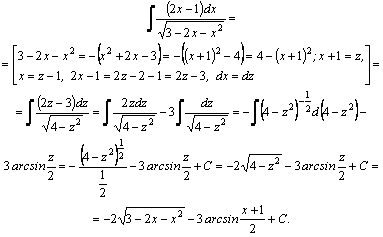 2. 2. 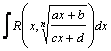 (под знаком интеграла–рациональная функция аргументов (под знаком интеграла–рациональная функция аргументов 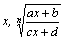 ). Интегралы такого вида вычисляются с помощью замены ). Интегралы такого вида вычисляются с помощью замены 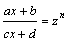 . В частности, в интегралах вида . В частности, в интегралах вида 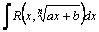 обозначают обозначают 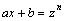 . Если подынтегральная функция содержит корни разных степеней: . Если подынтегральная функция содержит корни разных степеней: 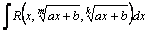 , то обозначают , то обозначают 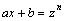 , где n– наименьшее общее кратное чиселm,k. Пример 1. , где n– наименьшее общее кратное чиселm,k. Пример 1. 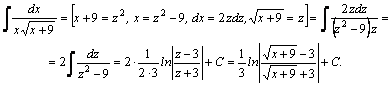 Пример 2. Пример 2.  –неправильная рациональная дробь, выделим целую часть: –неправильная рациональная дробь, выделим целую часть:
Получим 3.Интегралы вида Пример 1. Пример 2. |
44 
 45 Определённый интеграл
45 Определённый интеграл
Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция илифункционал, а вторая — область в множестве задания этой функции (функционала).
Определение
Пусть  определена на
определена на 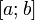 . Разобьём
. Разобьём 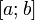 на части с несколькими произвольными точками
на части с несколькими произвольными точками 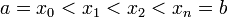 . Тогда говорят, что произведено разбиение
. Тогда говорят, что произведено разбиение 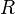 отрезка
отрезка 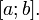 Далее выберем произвольную точку
Далее выберем произвольную точку 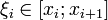 ,
, 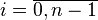 ,
,
Определённым интегралом от функции  на отрезке
на отрезке 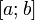 называется предел интегральных сумм при стремлении ранга разбиения к нулю
называется предел интегральных сумм при стремлении ранга разбиения к нулю 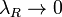 , если он существует независимо от разбиения
, если он существует независимо от разбиения 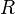 и выбора точек
и выбора точек 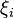 , то есть
, то есть
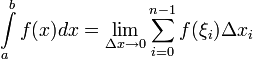
Если существует указанный предел, то функция  называется интегрируемой на
называется интегрируемой на 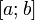 по Риману.
по Риману.
Обозначения
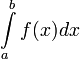
· 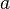 — нижний предел.
— нижний предел.
· 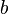 — верхний предел.
— верхний предел.
·  — подынтегральная функция.
— подынтегральная функция.
· 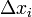 — длина частичного отрезка.
— длина частичного отрезка.
· 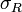 — интегральная сумма от функции
— интегральная сумма от функции  на
на 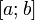 соответствующей разбиению
соответствующей разбиению 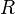 .
.
· 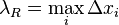 — максимальная длина част.отрезка.
— максимальная длина част.отрезка.
Свойства
Если функция  интегрируема по Риману на
интегрируема по Риману на 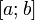 , то она ограничена на нем.
, то она ограничена на нем.
Геометрический смысл
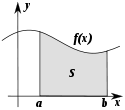

Определённый интеграл как площадь фигуры
Определённый интеграл 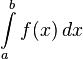 численно равен площади фигуры, ограниченной осью абсцисс, прямыми
численно равен площади фигуры, ограниченной осью абсцисс, прямыми  и
и 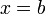 и графиком функции
и графиком функции  .
.
Теорема Ньютона — Лейбница
[править]
Материал из Википедии — свободной энциклопедии
(перенаправлено с «Формула Ньютона-Лейбница»)
Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.
Если  непрерывна на отрезке непрерывна на отрезке  и и 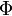 — ее любая первообразная на этом отрезке, то имеет место равенство — ее любая первообразная на этом отрезке, то имеет место равенство 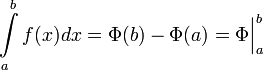 |
Доказательство
Пусть на отрезке  задана интегрируемая функция
задана интегрируемая функция  . Начнем с того, что отметим, что
. Начнем с того, что отметим, что
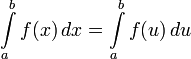
то есть не имеет никакого значения, какая буква ( 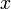 или
или 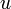 ) стоит под знаком
) стоит под знаком  в определенном интеграле по отрезку
в определенном интеграле по отрезку  .
.
Зададим произвольное значение 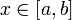 и определим новую функцию
и определим новую функцию 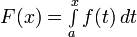 . Она определена для всех значений
. Она определена для всех значений 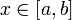 , потому что мы знаем, что если существует интеграл от
, потому что мы знаем, что если существует интеграл от  на
на  , то существует также интеграл от
, то существует также интеграл от  на
на 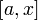 , где
, где 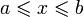 . Напомним, что мы считаем по определению
. Напомним, что мы считаем по определению
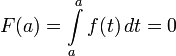 (1)
(1)
Заметим, что
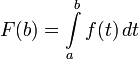
Покажем, что 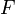 непрерывна на отрезке
непрерывна на отрезке  . В самом деле, пусть
. В самом деле, пусть 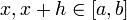 ; тогда
; тогда
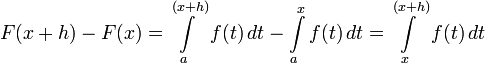
и если 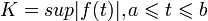 , то
, то
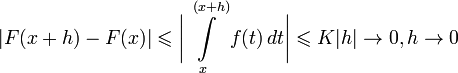
Таким образом,  непрерывна на
непрерывна на  независимо от того, имеет или не имеет
независимо от того, имеет или не имеет  разрывы; важно, что
разрывы; важно, что  интегрируема на
интегрируема на  .
.
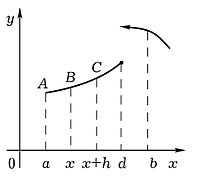
На рисунке изображен график  . Площадь переменной фигуры
. Площадь переменной фигуры 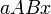 равна
равна 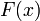 . Ее приращение
. Ее приращение 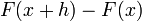 равно площади фигуры
равно площади фигуры 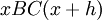 , которая в силу ограниченности
, которая в силу ограниченности  , очевидно, стремится к нулю при
, очевидно, стремится к нулю при 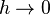 независимо от того, будет ли
независимо от того, будет ли 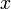 точкой непрерывности или разрыва
точкой непрерывности или разрыва  , например точкой
, например точкой 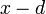 .
.
Пусть теперь функция  не только интегрируема на
не только интегрируема на 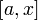 , но непрерывна в точке
, но непрерывна в точке 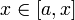 . Докажем, что тогда
. Докажем, что тогда 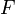 имеет в этой точке производную, равную
имеет в этой точке производную, равную
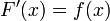 (2)
(2)
В самом деле, для указанной точки 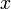
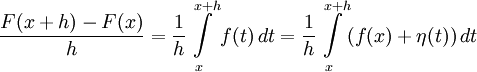
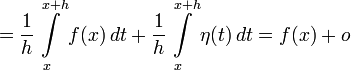 (1) ,
(1) , 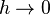 (3)
(3)
Мы положили 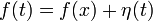 , а так как
, а так как 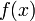 постоянная относительно
постоянная относительно 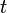 ,TO
,TO 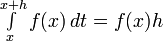 . Далее, в силу непрерывности
. Далее, в силу непрерывности  в точке
в точке 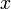 для всякого
для всякого 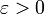 можно указать такое
можно указать такое 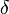 , что
, что 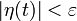 для
для 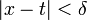 .
.
Поэтому
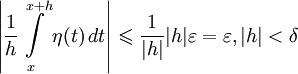
что доказывает, что левая часть этого неравенства есть о(1) при 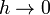 .
.
Переход к пределу в (3) при 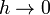 показывает существование производной от
показывает существование производной от 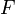 в точке
в точке 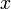 и справедливость равенства (2). При
и справедливость равенства (2). При 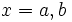 речь здесь идет соответственно о правой и левой производной.
речь здесь идет соответственно о правой и левой производной.
Если функция  непрерывна на
непрерывна на  , то на основании доказанного выше соответствующая ей функция
, то на основании доказанного выше соответствующая ей функция
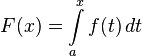 (4)
(4)
имеет производную, равную 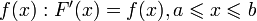 . Следовательно, функция
. Следовательно, функция 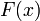 есть первообразная для
есть первообразная для  на
на  .
.
Это заключение иногда называется теоремой об интеграле с переменным верхним пределом или теоремой Барроу.
Мы доказали, что произвольная непрерывная на отрезке  функция
функция  имеет на этом отрезке первообразную, определенную равенством (4). Этим доказано существование первообразной для всякой непрерывной на отрезке функции.
имеет на этом отрезке первообразную, определенную равенством (4). Этим доказано существование первообразной для всякой непрерывной на отрезке функции.
Пусть теперь 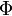 есть произвольная первообразная функции
есть произвольная первообразная функции 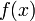 на
на  . Мы знаем, что
. Мы знаем, что 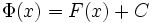 , где
, где 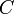 — некоторая постоянная. Полагая в этом равенстве
— некоторая постоянная. Полагая в этом равенстве  и учитывая, что
и учитывая, что 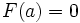 , получим
, получим 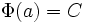 .
.
Таким образом, 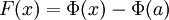 . Но
. Но
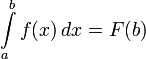
Поэтому
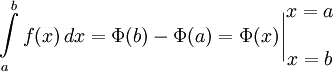
Несобственный интеграл
[править]
Материал из Википедии — свободной энциклопедии
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
· Предел a или b (или оба предела) являются бесконечными;
· Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].
| Содержание [убрать] · 1 Несобственные интегралы I рода o 1.1 Геометрический смысл несобственного интеграла I рода o 1.2 Примеры · 2 Несобственные интегралы II рода o 2.1 Геометрический смысл несобственных интегралов II рода o 2.2 Пример · 3 Отдельный случай · 4 Критерий Коши · 5 Абсолютная сходимость · 6 Условная сходимость · 7 См. также · 8 Список используемой литературы |
[править]Несобственные интегралы I рода
Пусть  определена и непрерывна на множестве от
определена и непрерывна на множестве от 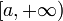 и
и 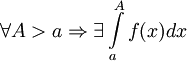 . Тогда:
. Тогда:
1. Если 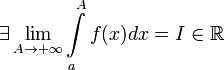 , то используется обозначение
, то используется обозначение 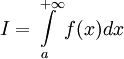 и интеграл называется несобственным интегралом Римана первого рода. В этом случае
и интеграл называется несобственным интегралом Римана первого рода. В этом случае 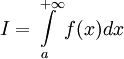 называется сходящимся.
называется сходящимся.
2. Если не существует конечного 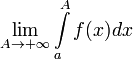 (
( 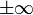 или
или 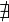 ), то интеграл
), то интеграл 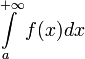 называется расходящимся к
называется расходящимся к 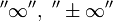 , или просто расходящимся.
, или просто расходящимся.
Пусть  определена и непрерывна на множестве от
определена и непрерывна на множестве от 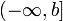 и
и 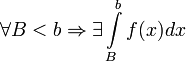 . Тогда:
. Тогда:
1. Если 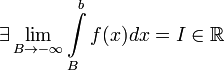 , то используется обозначение
, то используется обозначение 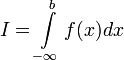 и интеграл называется несобственным интегралом Римана первого рода. В этом случае
и интеграл называется несобственным интегралом Римана первого рода. В этом случае 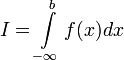 называется сходящимся.
называется сходящимся.
2. Если не существует конечного 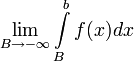 (
( 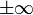 или
или 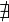 ), то интеграл
), то интеграл 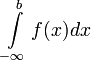 называется расходящимся к
называется расходящимся к 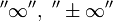 , или просто расходящимся.
, или просто расходящимся.
Если функция  определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
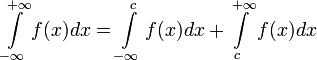 , где с — произвольное число.
, где с — произвольное число.
[править]Геометрический смысл несобственного интеграла I рода
Несобственный интеграл выражает площадь бесконечно длинной криволинейной трапеции.
[править]Примеры
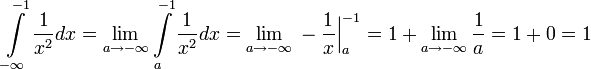
[править]Несобственные интегралы II рода
Пусть  определена на
определена на 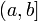 , терпит бесконечный разрыв в точке x=a и
, терпит бесконечный разрыв в точке x=a и 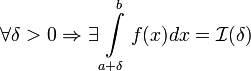 . Тогда:
. Тогда:
1. Если 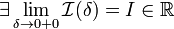 , то используется обозначение
, то используется обозначение 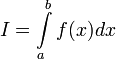 и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
2. Если 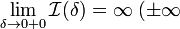 или
или 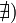 , то обозначение сохраняется, а
, то обозначение сохраняется, а 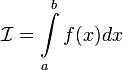 называется расходящимся к
называется расходящимся к 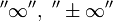 , или просто расходящимся.
, или просто расходящимся.
Пусть  определена на
определена на 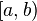 , терпит бесконечный разрыв при x=b и
, терпит бесконечный разрыв при x=b и 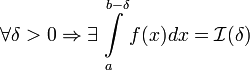 . Тогда:
. Тогда:
1. Если 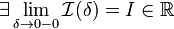 , то используется обозначение
, то используется обозначение 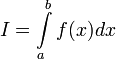 и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
2. Если 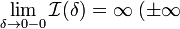 или
или 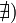 , то обозначение сохраняется, а
, то обозначение сохраняется, а 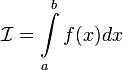 называется расходящимся к
называется расходящимся к 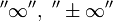 , или просто расходящимся.
, или просто расходящимся.
Если функция  терпит разрыв во внутренней точке
терпит разрыв во внутренней точке  отрезка
отрезка 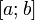 , то несобственный интеграл второго рода определяется формулой:
, то несобственный интеграл второго рода определяется формулой:
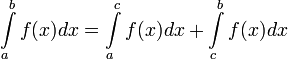
[править]Геометрический смысл несобственных интегралов II рода
Несобственный интеграл выражает площадь бесконечно высокой криволинейной трапеции
[править]Пример
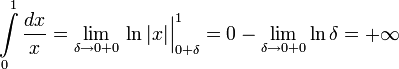
[править]Отдельный случай
Пусть функция  определена на всей числовой оси и имеет разрыв в точках
определена на всей числовой оси и имеет разрыв в точках 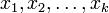 .
.
Тогда можно найти несобственный интеграл 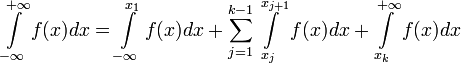
[править]Критерий Коши
1. Пусть  определена на множестве от
определена на множестве от 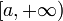 и
и 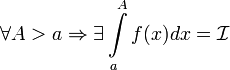 .
.
Тогда 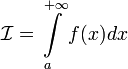 сходится
сходится 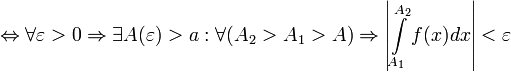
2. Пусть  определена на
определена на  и
и 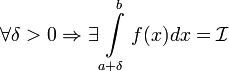 .
.
Тогда 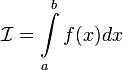 сходится
сходится 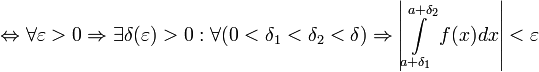
[править]Абсолютная сходимость
Интеграл 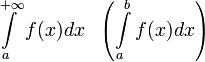 называется абсолютно сходящимся, если
называется абсолютно сходящимся, если 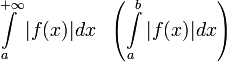 сходится.
сходится.
Если интеграл сходится абсолютно, то он сходится.
[править]Условная сходимость
Интеграл 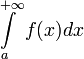 называется условно сходящимся, если
называется условно сходящимся, если 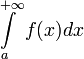 сходится, а
сходится, а 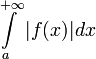 расходится.
расходится.
48 12. Несобственные интегралы.
 При рассмотрении определённых интегралов мы предполагали, что область интегрирования ограничена (более конкретно, является отрезком [a,b] ); для существования определённого интеграла
При рассмотрении определённых интегралов мы предполагали, что область интегрирования ограничена (более конкретно, является отрезком [a,b] ); для существования определённого интеграла 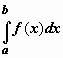 необходима ограниченность подынтегральной функции на [a,b]. Будем называть определённые интегралы, для которых выполняются оба эти условия (ограниченность и области интегрирования, и подынтегральной функции) собственными; интегралы, для которых нарушаются эти требования (т.е. неограничена либо подынтегральная функция, либо область интегрирования, либо и то, и другое вместе) несобственными. В этом разделе мы изучим несобственные интегралы.
необходима ограниченность подынтегральной функции на [a,b]. Будем называть определённые интегралы, для которых выполняются оба эти условия (ограниченность и области интегрирования, и подынтегральной функции) собственными; интегралы, для которых нарушаются эти требования (т.е. неограничена либо подынтегральная функция, либо область интегрирования, либо и то, и другое вместе) несобственными. В этом разделе мы изучим несобственные интегралы.
- 12.1. Несобственные интегралы по неограниченному промежутку (несобственные интегралы первого рода).
- 12.1.1. Определение несобственного интеграла по бесконечному промежутку. Примеры.
- 12.1.2. Формула Ньютона-Лейбница для несобственного интеграла.
- 12.1.3. Признаки сравнения для неотрицательных функций.
- 12.1.3.1. Признак сравнения.
- 12.1.3.2. Признак сравнения в предельной форме.
- 12.1.4. Абсолютная сходимость несобственных интегралов по бесконечному промежутку.
- 12.1.5. Признаки сходимости Абеля и Дирихле.
- 12.2. Несобственные интегралы от неограниченных функций (несобственные интегралы второго рода).
- 12.2.1. Определение несобственного интеграла от неограниченной функции.
- 12.2.1.1. Особенность на левом конце промежутка интегрирования.
- 12.2.1.2. Применение формулы Ньютона-Лейбница.
- 12.2.1.3. Особенность на правом конце промежутка интегрирования.
- 12.2.1.4. Особенность во внутренней точке промежутка интегрирования.
- 12.2.1.5. Несколько особенностей на промежутке интегрирования.
- 12.2.2. Признаки сравнения для неотрицательных функций.
- 12.2.2.1. Признак сравнения.
- 12.2.2.2. Признак сравнения в предельной форме.
- 12.2.3. Абсолютная и условная сходимость несобственных интегралов от разрывных функций.
- 12.2.4. Признаки сходимости Абеля и Дирихле.
12.1. Несобственные интегралы по неограниченному промежутку
(несобственные интегралы первого рода).
 12.1.1. Определение несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси
12.1.1. Определение несобственного интеграла по бесконечному промежутку. Пусть функция f(x) определена на полуоси 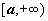 и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла
и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла 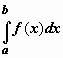 при
при 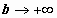 называется несобственным интегралом функции f(x) от a до
называется несобственным интегралом функции f(x) от a до 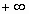 и обозначается
и обозначается 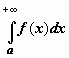 .
.
 Итак, по определению,
Итак, по определению, 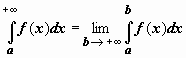 . Если этот предел существует и конечен, интеграл
. Если этот предел существует и конечен, интеграл  называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.
называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.
 Примеры: 1.
Примеры: 1. 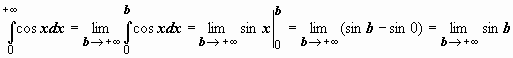 ; этот предел не существует; следовательно, исследуемый интеграл расходится.
; этот предел не существует; следовательно, исследуемый интеграл расходится.
 2.
2. 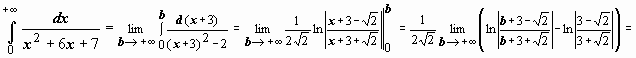
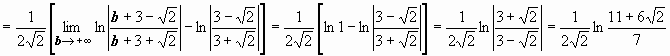 ; следовательно, интеграл сходится и равен
; следовательно, интеграл сходится и равен 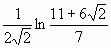 .
.
 Аналогично интегралу с бесконечным верхним пределом интегрирования определяется интеграл в пределах от
Аналогично интегралу с бесконечным верхним пределом интегрирования определяется интеграл в пределах от  до b :
до b : 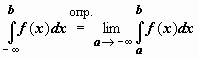 и в пределах от
и в пределах от  до
до  :
: 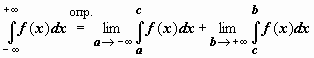 . В последнем случае f(x) определена на всей числовой оси, интегрируема по любому отрезку; c - произвольная (собственная) точка числовой оси; интеграл называется сходящимся, если существуют и конечны оба входящих в определение предела. Пользуясь свойством аддитивности определённого интеграла, можно показать, что существование конечных пределов и их сумма не зависят от выбора точки c.
. В последнем случае f(x) определена на всей числовой оси, интегрируема по любому отрезку; c - произвольная (собственная) точка числовой оси; интеграл называется сходящимся, если существуют и конечны оба входящих в определение предела. Пользуясь свойством аддитивности определённого интеграла, можно показать, что существование конечных пределов и их сумма не зависят от выбора точки c.
 Примеры: 3.
Примеры: 3. 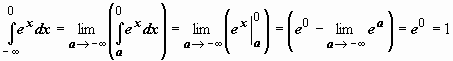 . Интеграл сходится.
. Интеграл сходится.
 4.
4. 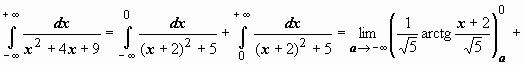
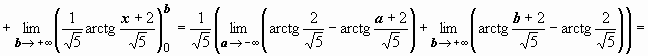
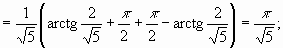 следовательно, интеграл сходится и равен
следовательно, интеграл сходится и равен 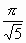 .
.
 Очевидно следующее утверждение, которое мы сформулируем для интеграла с бесконечным верхним пределом:
Очевидно следующее утверждение, которое мы сформулируем для интеграла с бесконечным верхним пределом: 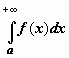 сходится тогда и только тогда, когда для любого c, удовлетворяющего неравенству c > a, сходится интеграл
сходится тогда и только тогда, когда для любого c, удовлетворяющего неравенству c > a, сходится интеграл 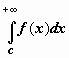 (док-во: так как при a < c < b по свойству аддитивности
(док-во: так как при a < c < b по свойству аддитивности 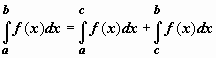 , и
, и 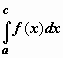 от b не зависит, то конечный предел при
от b не зависит, то конечный предел при 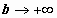 для интеграла в левой части существует тогда и только тогда, когда существует конечный предел для интеграла в правой части равенства).
для интеграла в левой части существует тогда и только тогда, когда существует конечный предел для интеграла в правой части равенства).
 12.1.2. Формула Ньютона-Лейбница для несобственного интеграла. В приведённых примерах мы сначала вычисляли с помощью первообразной функции определённый интеграл по конечному промежутку, а затем выполняли предельный переход. Объединим два этих действия в одной формуле. Символом
12.1.2. Формула Ньютона-Лейбница для несобственного интеграла. В приведённых примерах мы сначала вычисляли с помощью первообразной функции определённый интеграл по конечному промежутку, а затем выполняли предельный переход. Объединим два этих действия в одной формуле. Символом 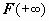 будем обозначать
будем обозначать 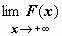 ; символом
; символом 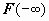 - соответственно,
- соответственно, 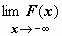 ; тогда можно записать
; тогда можно записать 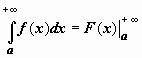 ,
, 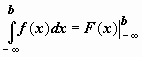 ,
, 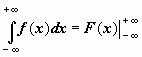 , подразумевая в каждом из этих случаев существование и конечность соответствующих пределов. Теперь решения примеров выглядят более просто:
, подразумевая в каждом из этих случаев существование и конечность соответствующих пределов. Теперь решения примеров выглядят более просто: 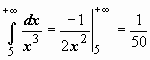 - интеграл сходится;
- интеграл сходится; 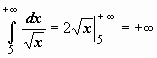 - интеграл расходится.
- интеграл расходится.
 Для несобственных интегралов применимы формулы интегрирования по частям и замены переменной:
Для несобственных интегралов применимы формулы интегрирования по частям и замены переменной: 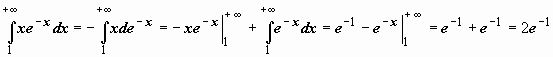 ; при замене переменной несобственный интеграл может преобразовываться в собственный. Так, например, вычислим интеграл:
; при замене переменной несобственный интеграл может преобразовываться в собственный. Так, например, вычислим интеграл: 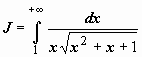 . Пусть
. Пусть 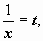
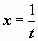 ,
, 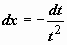 ; если
; если 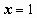 , то
, то 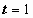 ; если
; если 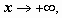 то
то 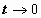 ;
; 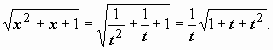 Поэтому
Поэтому 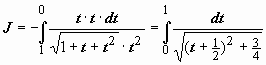 (это уже собственный интеграл) =
(это уже собственный интеграл) = 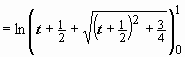
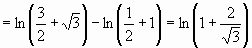 .
.
 12.1.3. Признаки сравнения для неотрицательных функций. В этом разделе мы будем предполагать, что все подынтегральные функции неотрицательны на всей области определения. До сих пор мы определяли сходимость интеграла, вычисляя его: если существует конечный предел первообразной при соответствующем стремлении (
12.1.3. Признаки сравнения для неотрицательных функций. В этом разделе мы будем предполагать, что все подынтегральные функции неотрицательны на всей области определения. До сих пор мы определяли сходимость интеграла, вычисляя его: если существует конечный предел первообразной при соответствующем стремлении ( 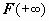 или
или 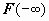 ), то интеграл сходится, в противном случае - расходится. При решении практических задач, однако, важно в первую очередь установить сам факт сходимости, и только затем вычислять интеграл (к тому же первообразная часто не выражается через элементарные функции). Сформулируем и докажем ряд теорем, которые позволяют устанавливать сходимость и расходимость несобственных интегралов от неотрицательных функций, не вычисляя их.
), то интеграл сходится, в противном случае - расходится. При решении практических задач, однако, важно в первую очередь установить сам факт сходимости, и только затем вычислять интеграл (к тому же первообразная часто не выражается через элементарные функции). Сформулируем и докажем ряд теорем, которые позволяют устанавливать сходимость и расходимость несобственных интегралов от неотрицательных функций, не вычисляя их.
 12.1.3.1. Признак сравнения. Пусть функции f(x) и g(x) интегр
12.1.3.1. Признак сравнения. Пусть функции f(x) и g(x) интегр

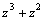
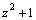
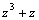
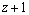
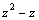
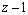

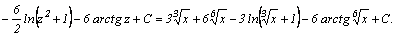
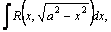
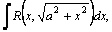
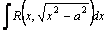 вычисляются с помощью тригонометрических подстановок:
вычисляются с помощью тригонометрических подстановок: