Необходимое условие экстремума
Экстремум функции
Необходимое условие экстремума
Функция g(x) в точке 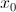 имеет экстремум(максимум или минимум), если функция определена в двухсторонней окрестности точки
имеет экстремум(максимум или минимум), если функция определена в двухсторонней окрестности точки 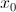 и для всех точек x некоторой области:
и для всех точек x некоторой области: 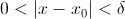 , выполнено соответственно неравенство
, выполнено соответственно неравенство
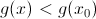 (в случае максимума) или
(в случае максимума) или 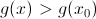 (в случае минимума).
(в случае минимума).
Экстремум функции находиться из условия: 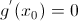 , если производная существует, т.е. приравниваем первую производную функции к нулю.
, если производная существует, т.е. приравниваем первую производную функции к нулю.
Достаточное условие экстремума
1) Первое достаточное условие:
Если:
а) f(x) непрерывная функция и определена в некоторой окрестности точки 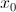 такой, что первая производная в данной точке равна нулю или не существует.
такой, что первая производная в данной точке равна нулю или не существует.
б) f(x) имеет конечную производную в окрестности задания и непрерывности функции
в) производная сохраняет определенный знак справа от точки 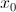 и слева от этой же точки, тогда точку
и слева от этой же точки, тогда точку 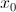 можно охарактеризовать следующим образом
можно охарактеризовать следующим образом 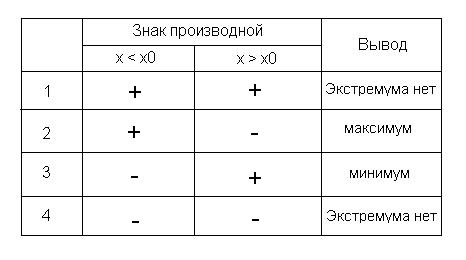
Это условие не очень удобное, так как нужно проверять множество условий и запоминать таблицу, однако если ничего не сказано о производных высших порядках, то это единственный способ найти экстремум функции.
2) Второе достаточное условие
Если функция g(x) обладает второй производной 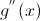 причем в некоторой точке
причем в некоторой точке 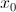 первая производная равна нулю, а вторая производная отлично от нуля. Тогда точка
первая производная равна нулю, а вторая производная отлично от нуля. Тогда точка 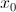 экстремум функции g(x), причем если
экстремум функции g(x), причем если 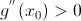 , то точка является максимумом; если
, то точка является максимумом; если 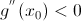 , то точка является минимумом.
, то точка является минимумом.
3) Третье достаточное условие
Пусть функция g(x) имеет в некоторой окрестности точки 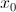 N производных, причем значение первых (N - 1)- ой и самой функции в этой точке равно нулю, а значение N-ой производной отлично от нуля. В таком случае:
N производных, причем значение первых (N - 1)- ой и самой функции в этой точке равно нулю, а значение N-ой производной отлично от нуля. В таком случае:
а) Если N - четно, то точка 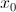 экстремум функции:
экстремум функции: 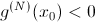 у функции точка максимума,
у функции точка максимума, 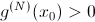 у функции точка минимума.
у функции точка минимума.
б) Если N - нечетно, то в точке 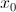 у функции g(x) экстремума нет.
у функции g(x) экстремума нет.
Абсолютный экстремум
Наибольшее(наименьшее) значение на сегменте [a;b] непрерывной функции g(x) достигается или в критической точке этой функции(т.е. где производная равна нулю или не существует), или в граничных точках а и b данного сегмента.
Основные понятия.
Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.
Обычно функция нескольких переменных задается явным аналитическим способом. Например: z=3x+5y2,u=xy+z2 и т.д.
Встречается также и неявное задание таких функций, например: z-2x-sinxy=0.
Упорядоченная пара чисел (x,y) может рассматриваться как точка на плоскости, т.е. Z есть функция точки (x,y).
Чтобы задать функцию z=f(x,y), надо не только указать правило нахождения zпо заданным x и y, но и то множество (называемое областью задания функции) пар значений, которые могут принимать аргументы x и y.
Например, функция z=  задана только при 1-y
задана только при 1-y  >0, т.е. внутри эллипса y2+4x2<1 с полуосями, а=0,5 и в=1 не включая точки, лежащие на эллипсе.
>0, т.е. внутри эллипса y2+4x2<1 с полуосями, а=0,5 и в=1 не включая точки, лежащие на эллипсе.



 Определение. Если каждой совокупности значений переменныхx,y,z…t соответствует определенное значение переменной w, то w называется функцией независимых переменных x,y,z…t и записываетсяw=f(x,y,z…t).
Определение. Если каждой совокупности значений переменныхx,y,z…t соответствует определенное значение переменной w, то w называется функцией независимых переменных x,y,z…t и записываетсяw=f(x,y,z…t).
Для функции трех переменных областью определения является упорядоченная тройка чисел (x,y,z), т.е. некоторая совокупность точек пространства. Область определения функции четырех и большего числа переменных не допускает простого геометрического истолкования. 
Функции двух переменных допускают графическую иллюстрацию. Графиком функции z=f(x,y), заданной на некотором множестве D точек плоскости ХОУ, называется множество точек (x,y,z) пространства, у которых (x,y) принадлежит D, а z=f(x,y). В наиболее простых случаях такой график представляет собой некоторую поверхность.
Например, графиком функции z=4-x2-y2 является параболоид.

Функции трех и большего числа переменных не имеют геометрического представления.
2.Непрерывность функции нескольких переменных.
Определение. Число А называется пределом функции f(M), где М(x1,x2,…xn)– точка n-мерного пространства, при стремлении точки М к точке М0(x10,x20,…xn0) любым образом, если для всякого сколь угодно малого  >0 существует такое число
>0 существует такое число  >0, что из условия
>0, что из условия  <
<  , где
, где  - расстояние между точками М и М0, следует
- расстояние между точками М и М0, следует  <
<  .
.
Обозначается:
А  .
.
Пусть z=f(x,y). Придадим x и y приращения  и
и  . Получим приращение
. Получим приращение  функции z=f(x,y). Если
функции z=f(x,y). Если
 , (1)
, (1)
т.е. бесконечно малым аргументам соответствует бесконечно малое приращение функции, то говорят, что функция непрерывна.
Распишем  x0+
x0+  y+
y+  -f(x0,y0) и положим x0+
-f(x0,y0) и положим x0+  x=x,y0+
x=x,y0+  ,то выражение(1) можно записать в виде
,то выражение(1) можно записать в виде
 f(x,y)=f(x 0,y0), (2)
f(x,y)=f(x 0,y0), (2)
т.е. непрерывность функции означает, что ее предел равен ее значению от пределов аргументов.
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области. Если в некоторой точке не выполняется условие (2), то эта точка называется точкой разрыва.
3 ПОВТОРНЫЙ ПРЕДЕЛ
- предел функции нескольких переменных, при к-ром предельный переход совершают последовательно по различным переменным. Пусть, напр., функция f двух переменных х и уопределена на множестве вида  , и пусть х 0, y0 - предельные точки соответственно множеств Xи Y или символы оо (в случае, когда m=1 или n=1, х 0 и соответственно y0 могут быть бесконечностями со знаком:
, и пусть х 0, y0 - предельные точки соответственно множеств Xи Y или символы оо (в случае, когда m=1 или n=1, х 0 и соответственно y0 могут быть бесконечностями со знаком:  ). Если при любом фиксированном
). Если при любом фиксированном  существует предел
существует предел
 (1) и у функции j(у).существует предел
(1) и у функции j(у).существует предел

то этот предел наз. повторным пределом
 (2)
(2)
функции f(x, у).в точке ( х 0, у 0). Аналогично определяется П. п.
 (3)
(3)
Если существует (конечный или бесконечный) двойной предел
 (4)
(4)
и при любом фиксированном  существует конечный предел (1), то существует и П. п. (2) и он равен двойному пределу (4).
существует конечный предел (1), то существует и П. п. (2) и он равен двойному пределу (4).
Если при каждом  существует предел (1), а при каждом
существует предел (1), а при каждом  существует предел
существует предел

и если при  функция f(x, у).стремится на Y к предельной функции j(у).равномерно относительно у, то оба П. п. (2) и (3) существуют и равны друг другу. Если множества XиYявляются множествами натуральных чисел, то функция f наз. в этом случае двойной последовательностью и значения аргументов пишут в виде индексов:
функция f(x, у).стремится на Y к предельной функции j(у).равномерно относительно у, то оба П. п. (2) и (3) существуют и равны друг другу. Если множества XиYявляются множествами натуральных чисел, то функция f наз. в этом случае двойной последовательностью и значения аргументов пишут в виде индексов:

а П. п.

наз. повторным и пределами двойной последовательности. Понятие П. п. обобщается на случай, когда X, Y и множество значений функции f являются подмножествами нек-рыхтопологич. пространств.
4 ДВОЙНОЙ ПРЕДЕЛ
- 1) Д. п. последовательности, предел двойной последовательности {х тп}, т, n=1, 2, ...,- число а, определяемое следующим образом: для любого е>0 существует такое Ne, что для всех m>Ne и n>Neвыполняется неравенство
Обозначение: 

Если для любого e>0 существует такое Ne, что для всех m>Ne и n>Ne выполняется неравенство |xmn|>e, то последовательность х тп имеет своим пределом бесконечность: 
Аналогично определяются бесконечные пределы

Д. п. последовательности является частным случаем Д. п. функции по множеству, а именно в случае, когда это множество состоит из точек плоскости с целочисленными координатами ти п. Поэтому между Д. п. последовательности и ее повторными пределами существует та же связь, что и в общем случае.
2) Д. п. функции - предел функции двух переменных, определяемый следующим образом. Пусть функция f(x, у)определена на множестве Е, расположенном в плоскостиXOY, а ( х 0, у 0)- его предельная точка. Число Аназ. Д. п. функции f(x, у )в точке ( х 0, у 0), или при  если для любого e>0 существует такое d>0, что для всех точек
если для любого e>0 существует такое d>0, что для всех точек  координаты к-рых удовлетворяют неравенствам
координаты к-рых удовлетворяют неравенствам 
выполняется неравенство

В этом случае пишут

Используя понятие предела последовательности, определение Д. п. функции можно сформулировать следующим образом:

если для любой последовательности

выполняется условие

Аналогично формулируются определения Д. п. функции при стремлении аргумента к бесконечности, а также определения бесконечных Д. п. функции.
Существует связь между Д. п. функции и повторным пределом функции в точке (x0, y0) или в  : пусть х 0 и у 0- предельные точки (конечные или бесконечные) для числовых множеств Xи У,
: пусть х 0 и у 0- предельные точки (конечные или бесконечные) для числовых множеств Xи У,  Если суще-
Если суще-
ствуетконечный или бесконечный Д. п. функции

и при любом  существует конечный предел
существует конечный предел

то существует и повторный предел

и он равен Д. п. функции.
Используя понятие окрестности, определению Д. п. функции можно придать следующий вид: пусть а- предельная точка (х 0, у 0 )множества Еили символ  , причем в последнем случае множество Енеограничено, А- число или один из символов
, причем в последнем случае множество Енеограничено, А- число или один из символов  тогда
тогда

если для любой окрестности О A точки или символа Асуществует такая окрестность О а числа или символа а, что для всех 
 выполняется условие
выполняется условие  В этом виде определение Д. п. функции переносится на случай, когда функция f определена на произведении топологич. пространств Xи Y,
В этом виде определение Д. п. функции переносится на случай, когда функция f определена на произведении топологич. пространств Xи Y,  а значения f(x, у )также принадлежат некоторому топологическиму пространству.
а значения f(x, у )также принадлежат некоторому топологическиму пространству.
34Частные производные.
Частной производной функции нескольких переменных по какой-нибудь переменной в рассматриваемой точке называется обычная производная по этой переменной, считая другие переменные фиксированными (постоянными). Например, для функции двух переменных  в точке
в точке  частные производные определяются так:
частные производные определяются так:
 ,
,
 ,
,
если эти пределы существуют. Величина  называется частным приращением функции z в точке
называется частным приращением функции z в точке  по аргументу
по аргументу  . Используются и другие обозначения частных производных:
. Используются и другие обозначения частных производных:
 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,  .
.
Символы  ,
,  ,
,  ,
,  как дроби трактовать нельзя (в этом отличие от случая одной переменной).
как дроби трактовать нельзя (в этом отличие от случая одной переменной).
Из определения следует геометрический смысл частной производной функции двух переменных: частная производная  - угловой коэффициент касательной к линии пересечения поверхности
- угловой коэффициент касательной к линии пересечения поверхности  и плоскости
и плоскости 
 в соответствующей точке.
в соответствующей точке.
Пользуясь понятием скорости изменения переменной, можно сказать, что частная производная  есть скорость изменения функции
есть скорость изменения функции  относительно
относительно  при постоянном
при постоянном  .
.
Из определения частных производных следует, что правила вычисления их остаются теми же, что для функций одной переменной, и только требуется помнить, по какой переменной ищется производная.
Пример 1. Если  , то
, то  ,
,  .
.
Пример 2. Если  , то
, то  ,
,  . Величина
. Величина  называется изотермическим коэффициентом упругости идеального газа.
называется изотермическим коэффициентом упругости идеального газа.
Аналогично определяются и обозначаются частные производные функции трех и большего числа независимых переменных.
ПОЛНОЕ ПРИРАЩЕНИЕ
функции нескольких переменных - приращение, приобретаемое функцией, когда все аргументы получают (вообще говоря, ненулевые) приращения. Точнее, пусть функция f определена в окрестности точки 
n-мерного пространства  переменных х 1,. . ., х п.Приращение
переменных х 1,. . ., х п.Приращение

функции f в точке x(0), где

наз. полным приращением, если оно рассматривается как функция n всевозможных приращений Dx1, . . ., Dxnаргументов х 1, . .., х п, подчиненных только условию, что точка x(0)+Dx принадлежит области определения функции f. Наряду с П. п. функции рассматриваются частные приращения Dxkf функции f в точке х (0) по переменной х k, т. е. такие приращения Df, для к-рыхDx уj=0, j=1, 2, . . ., k-1, k+1, . . ., п, k - фиксировано (k=1, 2, . . ., п).
35.
36.ТЕОРЕМА О ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ
Пусть y = f(u), а u= u(x). Получаем функцию y, зависящую от аргумента x: y = f(u(x)). Последняя функция называется функцией от функции или сложной функцией.
Областью определения функции y = f(u(x)) является либо вся область определения функции u=u(x) либо та ее часть, в которой определяются значения u, не выходящие из области определения функции y= f(u).
Операция "функция от функции" может проводиться не один раз, а любое число раз.
Установим правило дифференцирования сложной функции.
Теорема. Если функция u= u(x) имеет в некоторой точке x0 производную  и принимает в этой точке значение u0 = u(x0), а функция y= f(u) имеет в точке u0 производную y 'u= f'(u0), то сложная функция y = f(u(x)) в указанной точке x0 тоже имеет производную, которая равна y 'x= f '(u0)·u '(x0), где вместо u должно быть подставлено выражение u= u(x).
и принимает в этой точке значение u0 = u(x0), а функция y= f(u) имеет в точке u0 производную y 'u= f'(u0), то сложная функция y = f(u(x)) в указанной точке x0 тоже имеет производную, которая равна y 'x= f '(u0)·u '(x0), где вместо u должно быть подставлено выражение u= u(x).
Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x.
Доказательство. При фиксированном значении х0 будем иметь u0=u(x0), у0=f(u0). Для нового значения аргумента x0+Δx:
Δu= u(x0 + Δx) – u(x0), Δy=f(u0+Δu) – f(u0).
Т.к. u – дифференцируема в точке x0, то u – непрерывна в этой точке. Поэтому при Δx→0 Δu→0. АналогичноприΔu→0 Δy→0.
По условию  . Из этого соотношения, пользуясь определением предела, получаем (при Δu→0)
. Из этого соотношения, пользуясь определением предела, получаем (при Δu→0)
 ,
,
где α→0 приΔu→0, а, следовательно, ипри Δx→0.
Перепишем это равенство в виде:
Δy= y 'uΔu+α·Δu.
Полученное равенство справедливо и при Δu=0 при произвольном α, так как оно превращается в тождество 0=0. При Δu=0 будем полагать α=0. Разделим все члены полученного равенства на Δx
 .
.
По условию  . Поэтому, переходя к пределу при Δx→0, получим y 'x= y 'u·u 'x . Теорема доказана.
. Поэтому, переходя к пределу при Δx→0, получим y 'x= y 'u·u 'x . Теорема доказана.
Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от "внешней" функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от "внутренней" функции по независимой переменной.
Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y 'x осуществляется последовательным применением предыдущей теоремы.
По доказанному правилу имеем y 'x= y 'u·u 'x . Применяя эту же теорему для u 'x получаем  , т.е.
, т.е.
y 'x = y 'x· u 'v· v 'x = f 'u (u)·u 'v (v)·v 'x (x).
Примеры.
- y = sin x2. Тогда
 .
. -

-

-

Производная по направлению
[править]
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 июля 2012; проверки требуют 2 правки.
У этого термина существуют и другие значения, см. Производная.
В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.
Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.
Рассмотрим функцию 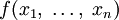 от
от 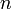 аргументов в окрестности точки
аргументов в окрестности точки 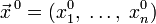 . Для любого единичного вектора
. Для любого единичного вектора 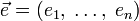 определим производную функции
определим производную функции  в точке
в точке 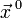 по направлению
по направлению 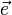 следующим образом:
следующим образом:
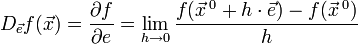
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора 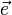 .
.
Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.
[править]Связь с градиентом
Производную по направлению дифференцируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:
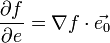 ,
,
где 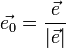 — орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлениемградиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора
— орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлениемградиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора 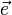 .
.
Теорема Ньютона — Лейбница
[править]
Материал из Википедии — свободной энциклопедии
(перенаправлено с «Формула Ньютона-Лейбница»)
Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.
Если  непрерывна на отрезке непрерывна на отрезке  и и 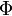 — ее любая первообразная на этом отрезке, то имеет место равенство — ее любая первообразная на этом отрезке, то имеет место равенство 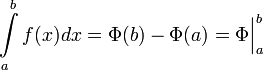 |
Доказательство
Пусть на отрезке  задана интегрируемая функция
задана интегрируемая функция  . Начнем с того, что отметим, что
. Начнем с того, что отметим, что
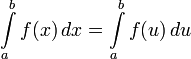
то есть не имеет никакого значения, какая буква ( 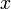 или
или 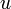 ) стоит под знаком
) стоит под знаком  в определенном интеграле по отрезку
в определенном интеграле по отрезку  .
.
Зададим произвольное значение 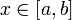 и определим новую функцию
и определим новую функцию 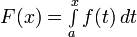 . Она определена для всех значений
. Она определена для всех значений 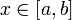 , потому что мы знаем, что если существует интеграл от
, потому что мы знаем, что если существует интеграл от  на
на  , то существует также интеграл от
, то существует также интеграл от  на
на 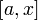 , где
, где 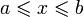 . Напомним, что мы считаем по определению
. Напомним, что мы считаем по определению
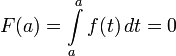 (1)
(1)
Заметим, что
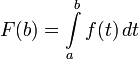
Покажем, что 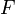 непрерывна на отрезке
непрерывна на отрезке  . В самом деле, пусть
. В самом деле, пусть 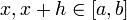 ; тогда
; тогда
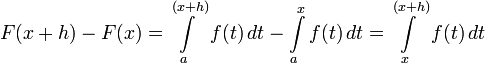
и если 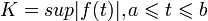 , то
, то
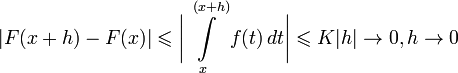
Таким образом, 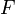 непрерывна на
непрерывна на  независимо от того, имеет или не имеет
независимо от того, имеет или не имеет  разрывы; важно, что
разрывы; важно, что  интегрируема на
интегрируема на  .
.
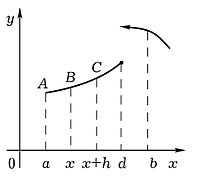
На рисунке изображен график  . Площадь переменной фигуры
. Площадь переменной фигуры 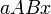 равна
равна 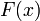 . Ее приращение
. Ее приращение 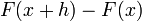 равно площади фигуры
равно площади фигуры 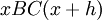 , которая в силу ограниченности
, которая в силу ограниченности  , очевидно, стремится к нулю при
, очевидно, стремится к нулю при 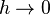 независимо от того, будет ли
независимо от того, будет ли 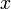 точкой непрерывности или разрыва
точкой непрерывности или разрыва  , например точкой
, например точкой 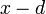 .
.
Пусть теперь функция  не только интегрируема на
не только интегрируема на 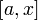 , но непрерывна в точке
, но непрерывна в точке 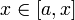 . Докажем, что тогда
. Докажем, что тогда 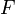 имеет в этой точке производную, равную
имеет в этой точке производную, равную
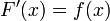 (2)
(2)
В самом деле, для указанной точки 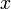
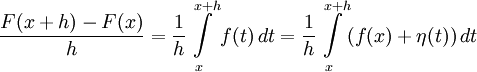
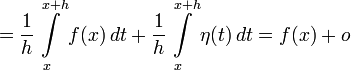 (1) ,
(1) , 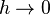 (3)
(3)
Мы положили 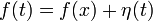 , а так как
, а так как 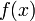 постоянная относительно
постоянная относительно 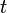 ,TO
,TO 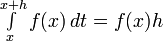 . Далее, в силу непрерывности
. Далее, в силу непрерывности  в точке
в точке 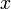 для всякого
для всякого 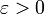 можно указать такое
можно указать такое 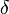 , что
, что 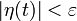 для
для 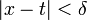 .
.
Поэтому
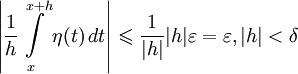
что доказывает, что левая часть этого неравенства есть о(1) при 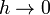 .
.
Переход к пределу в (3) при 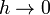 показывает существование производной от
показывает существование производной от 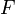 в точке
в точке 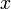 и справедливость равенства (2). При
и справедливость равенства (2). При 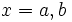 речь здесь идет соответственно о правой и левой производной.
речь здесь идет соответственно о правой и левой производной.
Если функция  непрерывна на
непрерывна на  , то на основании доказанного выше соответствующая ей функция
, то на основании доказанного выше соответствующая ей функция
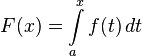 (4)
(4)
имеет производную, равную 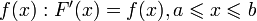 . Следовательно, функция
. Следовательно, функция 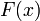 есть первообразная для
есть первообразная для  на
на  .
.
Это заключение иногда называется теоремой об интеграле с переменным верхним пределом или теоремой Барроу.
Мы доказали, что произвольная непрерывная на отрезке  функция
функция  имеет на этом отрезке первообразную, определенную равенством (4). Этим доказано существование первообразной для всякой непрерывной на отрезке функции.
имеет на этом отрезке первообразную, определенную равенством (4). Этим доказано существование первообразной для всякой непрерывной на отрезке функции.
Пусть теперь 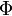 есть произвольная первообразная функции
есть произвольная первообразная функции 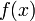 на
на  . Мы знаем, что
. Мы знаем, что 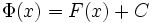 , где
, где 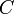 — некоторая постоянная. Полагая в этом равенстве
— некоторая постоянная. Полагая в этом равенстве  и учитывая, что
и учитывая, что 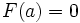 , получим
, получим 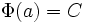 .
.
Таким образом, 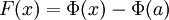 . Но
. Но
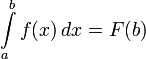
Поэтому
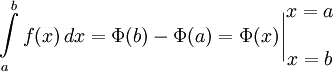
Несобственный интеграл
[править]
Материал из Википедии — свободной энциклопедии
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
· Предел a или b (или оба предела) являются бесконечными;
· Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].
| Содержание [убрать] · 1 Несобственные интегралы I рода o 1.1 Геометрический смысл несобственного интеграла I рода o 1.2 Примеры · 2 Несобственные интегралы II рода o 2.1 Геометрический смысл несобственных интегралов II рода o 2.2 Пример · 3 Отдельный случай · 4 Критерий Коши · 5 Абсолютная сходимость · 6 Условная сходимость · 7 См. также · 8 Список используемой литературы |
[править]Несобственные интегралы I рода
Пусть  определена и непрерывна на множестве от
определена и непрерывна на множестве от 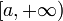 и
и 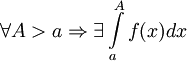 . Тогда:
. Тогда:
1. Если 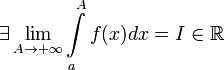 , то используется обозначение
, то используется обозначение 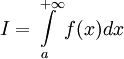 и интеграл называется несобственным интегралом Римана первого рода. В этом случае
и интеграл называется несобственным интегралом Римана первого рода. В этом случае 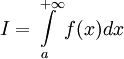 называется сходящимся.
называется сходящимся.
2. Если не существует конечного 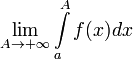 (
( 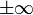 или
или 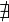 ), то интеграл
), то интеграл 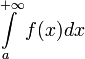 называется расходящимся к
называется расходящимся к 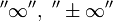 , или просто расходящимся.
, или просто расходящимся.
Пусть  определена и непрерывна на множестве от
определена и непрерывна на множестве от 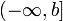 и
и 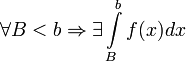 . Тогда:
. Тогда:
1. Если 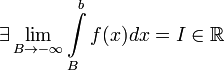 , то используется обозначение
, то используется обозначение 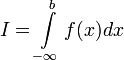 и интеграл называется несобственным интегралом Римана первого рода. В этом случае
и интеграл называется несобственным интегралом Римана первого рода. В этом случае 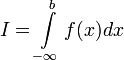 называется сходящимся.
называется сходящимся.
2. Если не существует конечного 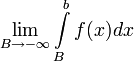 (
( 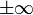 или
или 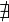 ), то интеграл
), то интеграл 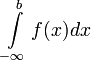 называется расходящимся к
называется расходящимся к 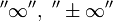 , или просто расходящимся.
, или просто расходящимся.
Если функция  определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
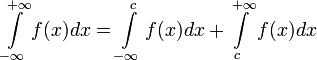 , где с — произвольное число.
, где с — произвольное число.
[править]Геометрический смысл несобственного интеграла I рода
Несобственный интеграл выражает площадь бесконечно длинной криволинейной трапеции.
[править]Примеры
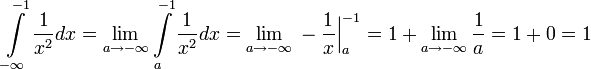
[править]Несобственные интегралы II рода
Пусть  определена на
определена на 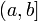 , терпит бесконечный разрыв в точке x=a и
, терпит бесконечный разрыв в точке x=a и 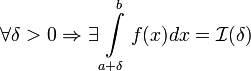 . Тогда:
. Тогда:
1. Если 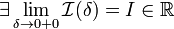 , то используется обозначение
, то используется обозначение 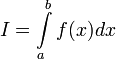 и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
2. Если 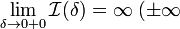 или
или 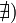 , то обозначение сохраняется, а
, то обозначение сохраняется, а 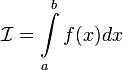 называется расходящимся к
называется расходящимся к 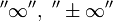 , или просто расходящимся.
, или просто расходящимся.
Пусть  определена на
определена на 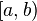 , терпит бесконечный разрыв при x=b и
, терпит бесконечный разрыв при x=b и 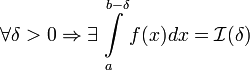 . Тогда:
. Тогда:
1. Если 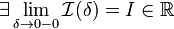 , то используется обозначение
, то используется обозначение 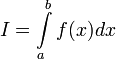 и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
2. Если 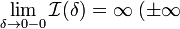 или
или 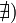 , то обозначение сохраняется, а
, то обозначение сохраняется, а 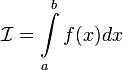 называется расходящимся к
называется расходящимся к 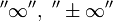 , или просто расходящимся.
, или просто расходящимся.
Если функция  терпит разрыв во внутренней точке
терпит разрыв во внутренней точке  отрезка <
отрезка <
