Теоремы об изменении импульса и момента импульса.
Теорема: Изменение импульса в единицу времени=действующ силе на мат (.) в данный момент.  .
.  -кинемат хар-ка.
-кинемат хар-ка.
 ,
,  ,
,  -диф форма.
-диф форма.  интегр форма. Под дейст силы и с временем
интегр форма. Под дейст силы и с временем  мат (.) преобр импульс
мат (.) преобр импульс  ,
,  (
(  ) Следствие: Если мат (.) не действ никакая сила, то вып-ся з-н сохр. ипульса
) Следствие: Если мат (.) не действ никакая сила, то вып-ся з-н сохр. ипульса  из котор след
из котор след  или , если на мат (.) не действ сила, то она движ равном и прямолин(
или , если на мат (.) не действ сила, то она движ равном и прямолин(  . Теорема: Изменение момента импульса в ед времени = моменту силы, действ на мат (.). Следствие: Если момент силы
. Теорема: Изменение момента импульса в ед времени = моменту силы, действ на мат (.). Следствие: Если момент силы  , то
, то  , след
, след  , если на мат (.) нет действия момента силы,то в этом случ вып-ся закон сохр момента импульса.
, если на мат (.) нет действия момента силы,то в этом случ вып-ся закон сохр момента импульса.
Свойства потенциальных полей
Поле наз. потенциальным, если для этого силового поля выполняется соотношение:  =-
=-  U
U
F-сила,U-потенц. энергия взаимодействия материальной точки с потен. полем.
 ,
,  -единицы вектора
-единицы вектора
(  )=1, (
)=1, (  )=1, (
)=1, (  )=1, (
)=1, (  )=0, (
)=0, (  )=0, (
)=0, (  )=0
)=0
 =x
=x  +z
+z  ;(
;(  )=
)=  =3
=3
 )=
)=  x2+y2+z2)=
x2+y2+z2)= 
 =
=  ,r = √(x2+y2+z2)
,r = √(x2+y2+z2)
 =-
=- 
Примеры потенциальных полей
1.Кулоновское электростатическое поле, т.е.это поле кот. создается пакоющимися точечными зарядами. 
Из теории электричества:  ,
,  ,
,  =-
=- 
U=q  =
=  , -
, -  =
= 
Вывод: электростатич. кулоновское поле явл. потенциальным.
x2+y2+z2=с2- ур-е сферы.
2.Постоянная гравитационного поля
 =
=  , U=
, U= 
U=  ,R
,R 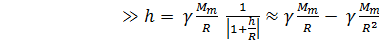
 =m
=m  = -
= -  ,mg=
,mg=  ,
,  , U=mgz
, U=mgz  , F= -
, F= - 
Потенциальная энергия потен. поля опред. С точностью до константы.
U= mgz=const ,z=c’
Вывод: эквипотенциальными плоскостями поля сил тяжести явл.плоскости.
3. Поле упругих сил
F= -k(x-l) = -kx ,z=x-l ;  ,
,  , U=
, U=  ,
, 
Эквипотенц. поверх-ми поля упругих сил явлю сферы.
Теорема об изменении кинетической энергии материальной точки.
Поле наз. потенциальным, если для этого силового поля выполняется соотношение:  =-
=-  U
U
F-сила,U-потенц. энергия взаимодействия материальной точки с потен. полем.
m  , m(
, m(  ,
,  (
(  )=(
)=(  )=
)=  =
=  ,
, 
Изменение кинет. энергии в единицу времени равно мощности или работе совершаемой в единицу времени наз. материальной точкой.
 =-
=-  U
U  ,
,  = -
= -  ,
,  (дифер-е сложной формы)
(дифер-е сложной формы)
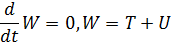
W=const- полная энергия
Теорема об изменении импульса механ. системы.
 +
+ 
 +
+ 
 +
+  +
+ 
 =
=  , p=
, p=  ,
, 
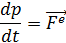
Изменение импульса в единицу времени мех. сис-мы равно суммарному действию внешних сил на эту мех. сис-му.
Следствие:
1.  ,
,
 ,
,  =
= 
Закон сохранения суммарного импульса.
2. Определение центра масс мех. сис-мы:

 и тогда уравнение
и тогда уравнение  примет вид:
примет вид:  .
.  - равномерное прямолинейное движение., или закон сохранения скорости центра масс механ системы. Система центра масс или система центра инерции.
- равномерное прямолинейное движение., или закон сохранения скорости центра масс механ системы. Система центра масс или система центра инерции.  при
при  получим :
получим :  ;
;  , сумма импульсов механич системы равна 0:
, сумма импульсов механич системы равна 0: 
Выделение движения центра масс и относительного движения механической системы.
Центр масс – воображаемая точка ,которая как бы обладает массой, равной массе всей системы и положение которой определяется радиус-вектором: 
 и тогда уравнение
и тогда уравнение  примет вид:
примет вид:  .
.  - равномерное прямолинейное движение., или закон сохранения скорости центра масс механ системы. Система центра масс или система центра инерции.
- равномерное прямолинейное движение., или закон сохранения скорости центра масс механ системы. Система центра масс или система центра инерции.  при
при  получим :
получим :  ;
;  , сумма импульсов механич системы равна 0:
, сумма импульсов механич системы равна 0: 
