Законы Ньютона. Методы решения задач в мех Ньютона.

Осн. пон-я теор. физ.

Классич. механ. заним-ся движен. микроскоп. тел, скорости к-ых много меньше скор. света. Материал (.)(частица) – размер котор. можн. пренебр., по сравнению с разн. характер-е это тело,или (.) обладающ.массой. Положением мат. (.) и в прост-ве зад-ся в опред. выбран. системе координат. В клас. мех. реализ. в 3х мерной и евклидово = > Расстояние между 2мя (.) и не измен. при повороте системы координат или при перем. нач. системы отсчета. Событие обозначается местом и моментом. Совокупность событий образ. многообраз. 4х мерн. пространства времени. В класич. мех. это 4х мерн. многобр расчепл. на 3х мерный евклид и ось. В класич. мех. св-ва 3х мерн. простр. не завис. от св-в времени. Расстояние между (.) и измерения независимо, т.е. св-ва пр-ва и времени не связ. др. с др., но это спр. не в реалит. Поскольку время и пр-во отделили друг от друга механ., то можно в этом случае ввести понятие абс. пр-ва и абс вр-ни: время вступает как пар-р, а радиус ­– вектор зав. y(t),z(t),x(t), Если бы вы рассм. пр-во как единое, то x{x,y,z,ct}. Механическое движение-изменение с теч. Времени взаимного пол-я в пр-ве мат. тел. Тело отсчета - тело, относит к-ого опред. событие связан. с др. телами. Тель отсчёта: СК с началом совмещ. с телом отсчет и часы в сов-ти обр. систему отсчета. Механическая система - сов-ть материал.(.) и в неретешивис. массы мех.сис-мы масс матер. (.)ы. Состояния мех. системы опред. заданием всех коорд. матер. (.) и в данный момент. Основная задача механики состоит в том, что бы по заданию в данный момент времен. состояния опред. сост. Решить осн. задачу: означ. опред. дв-е сис-мы, т.е. опред.x(t),y(t),z(t) в данный момент времени: x(t),y(t) и z(t) сост. реш-е ур-е дв-е в виде ДУ т. обр. решить задачу механическим означ: 1)получить вид ур-я дв-я мех. сис-мы. 2)решить эти ур-я, что бы получ. зав. корд. от времени. Положен. Матер. (.)в данный момент времени опред. с пом. µ конец рад. при дв-е мат. (.) опис. в пр-ве кривую, наз. траекторией т. обр. Траектория-геом. место положения движения мат.(.) в опред. сис-ме отсчета. Инертность-свойство мат. тела сохр. сост-я покоя равн. или прямого действия. Инерц. СО – Со относит. к-ой мат.(.) движ. Равном и прямолинейном 2 СО наз. инерциал., если они движ. с Const скоростями.

2.Принцип относительности Галилея. Преобразования Галилея.

З-ны физики не зависят от выбора инерциальн. системы отсчёта. З-ны ньютона не завис от инерц со. V-скорость штриховой со , , . В случае, когда инерц. со и тело движ-ся с малой скоростью, скор-ти склад-ся лин образом. Преобразования Галилея: , , . Векторная ф-ма: . С и тоже самое. Движение одной со относ другой должн быть равным и прямолин. 2ой з-н Ньютона инвареантен(НЕИЗМЕН ОТНОСИТ ПРЕОБР ГАЛИЛЕЯ) 3ий относ одной к другой со.

Вопрос

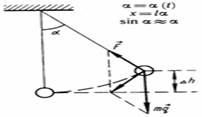
Будем рассматривать движение маятника при условии, что угол отклонения мал, тогда, если измерять угол в радианах, справедливо утверждение: На тело действуют сила тяжести и сила натяжения нити. Равнодействующая этих сил имеет две составляющие: тангенциальную, меняющую ускорение по величине, и нормальную, меняющую ускорение по направлению (центростремительное ускорение, тело движется по дуге).Т.к. угол мал, то тангенциальная составляющая равна проекции силы тяжести на касательную к траектории: Угол в радианах равен отношению длины дуги к радиусу (длине нити), а длина дуги приблизительно равна смещению (x »s): Сравним полученное уравнение с уравнением колебательного движени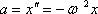

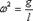
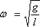
Аналогичные вычисления можно проделать с помощью закона сохранения энергии. Учтем, что потенциальная энергия тела в поле тяготения равна а полная механическая энергия равна максимальной потенциальной или кинетической: Запишем закон сохранения энергии и возьмем производную от левой и правой частей уравнения: 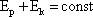Т.к. производная от постоянной величины равна нулю, то Производная суммы равна сумме производных: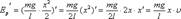

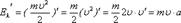
Следовательно

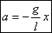
12 . Описание упругих колебаний материальной точки на основании 2-го закона Ньютона и закона сохранения энергии. ; ; механ.Ньютона ; ; ; ; ; ; ; ; ; ; ; ; ; . ; ; ; ; -полная энергия; = - уравнение движения ; ; ; y= dy=dz; ; C =-2 ; ; ; ;

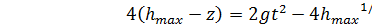13.Связи. Уравнения связей. -уравнение связи ;Связь– это совокупность тел огранич.движение определенного тела. Связи кот. огранич.движение тел описываются аналитическими ур-ями кот. наз.ур-ями связи. Рассмотрим движ. Одной мат.т.движ. кот.ограничена связеми. f( =0; где t-время, ( =0, ( =0, ( =0, ( =0; f(x)=0, f(x)=x-l; уравнение плоскости является связью -функции связи

Для круга

Каждая определенная связь ограниченная движением мат.точки уменьшает число степеней свободы . стационарные связи –это такие связи ф-ии кот. явно не зависят от времени , в противном случае если ф-ии зависят от времени то она стационарная.В механ.использ. голономные и неголономныесвязи . Голономн.наз.связи кот. можно определить аналитич.ур-ями и эти ур-ия описываются опред. ур-ями поверхностей в противном случае связь явл.неголономной.силы кот.обусловленны действия связи наз.пассивными или реактивными силими. Активныминаз.силы кот вызывают ускорение мат. точек. Если мат.система состоит из N мат.точек 3N-P=r;Определение числа механ.системы с учетом связи огранич.движ.мех.системы. Виды перемещений: Действительные перемещения-это перемещение мат.точки под действием активных и пассивных сил. Возможные-это перемещ.кот.огран.связями действующ.на мат. точку или тело. Виртуальные –это вооброжаемые перемещ. кот. обусловл.действием активных и пассивных сил.

14.Элементы дифференцирования и варьирования в теоретической мех. ; dz=vdt; z=z(t); ; Если в данный фиксированный момент времени переход от одной траектории к другой : то эта операция перехода от одной траектории к другой близко расположенной относительно основной траектории наз.варьированием. -варьирование преременных. С помощью операции варьирования определяется виртуальное варьирование. Если речь идет о вычислении вариации ф-ии зависящей от вариации ; ; ; ( =0, ; ( = ; ( = ; ; = ; =

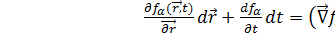15. Метод неопределенных множителей Лагранжа. Рассм. Мех. состоящую из N мат.т.на это на мех.систему наложено pсвязей(идеальных). r=3N-p Связи описываются ур-ями связи ; все связи идеальны . Вычислим вариации ф-ции : 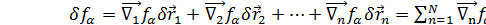; умножим ур-ние на и сложим все ур-ия : ; ; Если бы число степеней свободы мех. системы 3N то каждая было бы независимым и тогда выражение в квадратных скобках можно было бы прировнять к нулю, но число степеней свободы меньше 3N и равно 3N-p где р – число ур-ний связи.поэтому мы такого утверждения сделать не можем т.к. неопределенные множители то мы подберем их таким образом что бы в каждом слогаемым выражение в квадратных скобках=0; из явного вида ф-лы связь реакции связи с ур-ями (функциями связи). ; - ур-ние Лагранжа 1-го рода.

16. Ур-е Лагранжа 1-го рода.

Рассм. мех.сис-му, состоящ. из N материальн.точек. На эту мех.сис-му наложено р-связей идеальных. Число степеней свободы r = 3N-p.

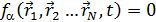(8.1) a=1,2…p.

Вычислим теперь вариацию функций ур-я (8.1):

d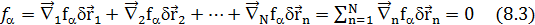

Умножим теперь кажд.ур-е (8.3) на множитель 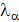и сложим эти ур-я,тогда получ.:

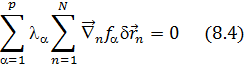
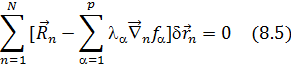
Если бы число степеней свободы мех.сис-мы было 3N, то каждая d 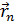было бы независ. и тогда выраж-е в [ ] скобках можно было бы приравнять к 0, но число степеней свободы меньше 3N и равно 3N-p, где р- число ур-й связи, поэтому такого утверждения мы сделать не можем, однако, поскольку 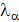неопред.множители, то мы подберем их т.образом, чтобы в каждом слагаемом (8.5) выр-е в [ ] равнялись нулю. След-но из нашего утверждения следует, что

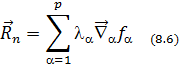
Из явного вида ф-лы (8.6) следует связь реакции связи с ур-ями (ф-циями) связи

ур-е Д*аламбера.

Если учтем ур-е (8.6), то получ.

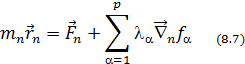
Это и есть ур-е Лагранжа 1-го рода.

Общее ур-е механики.

реакция связи, наз.идеальной для одной матер.точки,если выполн.ур-е:

(

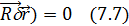
Принцип Д*аламбера:

При движ-ии матер.точки сил действующих на матер.точку =0

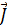= -m

Если ур-е (7.9) скалярно умножим на d , то ( =0 (7.10), это ур-е наз.общим ур-ем механики для одной матер.точки.

Для сис-мы состоящ.из n матер.точек принцип Д*аламбера будет записан так:

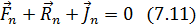n=1,2…

Если умножим (7.11) скалярно на d 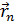, а затем проссумируем.то получим:

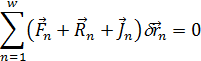
Если связь идеальна, то это ур-е запиш. В виде:

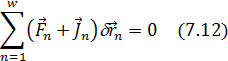
Общее ур-е механики

Вариационный принцип.

Урав. Лагранжа-Эйлера

Пример:

– ф-я

действия.

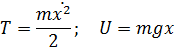
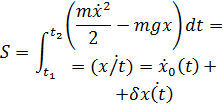
Где будет малая величина . При дальнейших вычислениях будем ограничиваться 1-м порядком малости по .

.

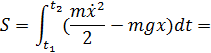
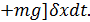
Ф-я действия будет min,если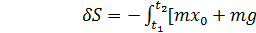

Поскольку пределы интегрирования по времени выбраны произвольным образом, то этот интеграл =0,если подинтеграл. выраж. =0. Поскольку отлично от 0, то выраж.в квадратной скобке=0.

Каждой степени свободы ставиться в соответствие независящая обобщённая координата. В общем случае обобщ. Корд.мех. сист. все r обобщ. коорд. независимы друг от друга. Соответственно обобщ. скорости они также независимы друг от друга.

Ф-я Лагранжа(L) назыв. разность T-U, где T-кинитич. энергия, U- потенц. энерг. системы.

L= T-U

T=T ( ,

U=U ( , то ф-я Лагранжа будет ф-я обобщ.коорд. и скоростей.

L=L(

Ур-я Лагранжа-Эйлера.

Ф-я Лагр. Для мех. сист.с одной степенью свободы будет: L=T-U=L( q,

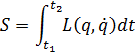
Для получения ур-я движ. мех.сист. 1-й степени свободы воспользуемся принципом наименьшего действия (вариационный принцип).

(поскольку операция варьирования и дефференц.по времени, а следоват.и интегриров. по времени перестановочные операции, то операц. варьирования поднесём под , тогда)=

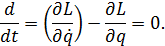
Ур-я Лагранжа-Эйлера, движущ-ся точки в центрально симметр.поле:

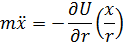
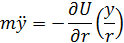
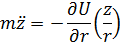
Законы Кеплера.

Первый закон Кеплера (закон эллипсов).Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.Форма эллипса и степень его сходства с окружностью характеризуется отношением , где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось. Величина e называется эксцентриситетом эллипса. При c = 0 и e = 0 эллипс превращается в окружность. Второй закон Кеплера (закон площадей).Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные времена радиус-вектор, соединяющий Солнце и планету, описывает равные площади. Третий закон Кеплера (гармонический закон)Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.

, где T₁ и T₂ — периоды обращения двух планет вокруг Солнца, а a₁ и a₂ — длины больших полуосей их орбит.Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты: , где M — масса Солнца, а m₁ и m₂ — массы планет.

38 39 40

Только 43

Ненужно

Вопрос

В гамильтоновой механике каноническое преобразование — это любое преобразование фазового пространства системы, сохраняющее его симплектическую структуру.Канонические преобразования обычно задаются производящей функцией. Пусть F(q,Q,t) — произвольная невырожденная функция старых координат, новых координат и времени: Тогда она задаёт каноническое преобразование по правилу где (q,p) — старые координаты и импульсы системы, а (Q,P) — новые координаты и импульсы.Действие, выраженное как функция координат и импульсов конечной точки задаёт каноническое преобразование гамильтоновой системы.

Опрос 45

ГАМИЛЬТОНА - ЯКОБИ УРАВНЕНИЕ - дифференциальное ур-ние в частных производных 1-го порядка, описывающее движение голономных механич. систем под действием потенц. сил. Чтобы составить Г.- Я. у., необходимо для данной механич. системы знать Гамильтона функцию H(qi, pi, t), где qi и рi- - канонич. переменные: обобщённые координаты и обобщённые импульсы, a t - время. Тогда Г.- Я. у. будет иметь вид

где правая часть представляет собой выражение ф-ции H, в к-ром все pi заменены на , a S - подлежащая определению ф-ция координат qi и времени t, представляющая собой действие по Гамильтону; иногда ф-цию S (qi, t)наз. главной ф-цией Гамильтона.

В частном случае при движении одной материальной точки в силовом поле, определяемом силовой ф-цией U(x, у, z, t), Г.- Я. у. имеет вид

,

где т - масса точки, х, у, z - её координаты.

Г.- Я. у. непосредственно связано с Гамильтона уравнениями ,к-рые с матем. точки зрения являются для ур-ния (1) ур-ниями характеристик.

Чтобы с помощью Г.- Я. у. найти закон движения механич. системы, надо определить полный интеграл ур-ния (1), т. е. его решение, содержащее столько постоянных интегрирования, сколько в ур-нии независимых переменных. Этими переменными являются координаты qi и время t; число их равно s+1, где s - число степеней свободы системы. Следовательно, полный интеграл ур-ния (1) должен содержать s+l постоянную, из к-рых одна, как аддитивная, может быть отброшена, и имеет вид

Если решение Г.- Я. у. в виде (2) будет найдено, то, составив s равенств

где - новые произвольные постоянные, получим s алгебраических (недифференциальных) ур-ний, левые части к-рых содержат qi, и t и из к-рых можно определить qi в виде

Значения др. группы канонич. переменных рi находят из равенств

Ур-ния (4), выражающие qi как ф-ции t, и определяют положение механич. системы в любой момент времени, т. е. закон её движения. Входящие сюда постоянные и находят подстановкой начальных данных в равенства (4) и (5).

Если ф-ция Гамильтона H явно не содержит время, что, в частности, имеет место для консервативных систем, то S можно искать в виде

где h - постоянная, равная полной энергии системы, a S0 - величина, наз. укороченным действием (действием по Лагранжу) или характеристич. ф-цией и определяемая как полный интеграл ур-ния в частных производных

в виде Тогда полный интеграл Г.- Я. у. будет и закон движения системы определится в соответствии с (3) из равенств

Кинем.ур-е Эйлера

Ориентация вращ-ия ТВ.тела опр-ся углами Эйлера:

-прецесионный угол, θ -нутационный,

ψ -угол собств.вращения ТВ.тела.

В мех-ке вращ.тв.тела эти 3 угла явл.обобщ.коорд.и

Они явл.3 степ.свободы ТВ.тела.

X=L-ось Lили ось узлов

Нутационное вращение со временем мен-ся(θ);

I1=I2=I3;L=T-U=

=L( θ , ψ, θ , ψ); θ , ψ;

W=W1n1+W2n2+W3n3= n3+ θ n3+ ψ n3;W3= ψ+ θ;

N3=an3+bn3;n1=an2+bn1;a=sin ψ;

B=cos ψ;W1= sin ψ sin θ+ θ cos ψ;

W2= cos ψ sin θ- θ sin ψ

Кинем. перем-е рел.мех-ки

х

\

Где β=

х1=

х2=х2

х3=х3

х4=

х1=

y=y

z=z

ict=

t=

β

x=x-vt -преобр-я Галл-я

y=y для ч-цы с мал.ско-

z=z ростями

t=t

59.Движ.релят.заряж.частицы в э\м поле.

Исп.Лагранжев формализм:

L=πv-H=

Ф-ла Лагранжа для свободно движ.ч-цы:

L=

. π; для

своб.движ.ч-цы буд.циклич.

Ур. Движ.для своб.движ.ч-цы: .

Рассм.прим.дв-я зар.ч-цы в пост.эл.поле:

L=

.

. .

Осн. пон-я теор. физ.

Классич. механ. заним-ся движен. микроскоп. тел, скорости к-ых много меньше скор. света. Материал (.)(частица) – размер котор. можн. пренебр., по сравнению с разн. характер-е это тело,или (.) обладающ.массой. Положением мат. (.) и в прост-ве зад-ся в опред. выбран. системе координат. В клас. мех. реализ. в 3х мерной и евклидово = > Расстояние между 2мя (.) и не измен. при повороте системы координат или при перем. нач. системы отсчета. Событие обозначается местом и моментом. Совокупность событий образ. многообраз. 4х мерн. пространства времени. В класич. мех. это 4х мерн. многобр расчепл. на 3х мерный евклид и ось. В класич. мех. св-ва 3х мерн. простр. не завис. от св-в времени. Расстояние между (.) и измерения независимо, т.е. св-ва пр-ва и времени не связ. др. с др., но это спр. не в реалит. Поскольку время и пр-во отделили друг от друга механ., то можно в этом случае ввести понятие абс. пр-ва и абс вр-ни: время вступает как пар-р, а радиус ­– вектор зав. y(t),z(t),x(t), Если бы вы рассм. пр-во как единое, то x{x,y,z,ct}. Механическое движение-изменение с теч. Времени взаимного пол-я в пр-ве мат. тел. Тело отсчета - тело, относит к-ого опред. событие связан. с др. телами. Тель отсчёта: СК с началом совмещ. с телом отсчет и часы в сов-ти обр. систему отсчета. Механическая система - сов-ть материал.(.) и в неретешивис. массы мех.сис-мы масс матер. (.)ы. Состояния мех. системы опред. заданием всех коорд. матер. (.) и в данный момент. Основная задача механики состоит в том, что бы по заданию в данный момент времен. состояния опред. сост. Решить осн. задачу: означ. опред. дв-е сис-мы, т.е. опред.x(t),y(t),z(t) в данный момент времени: x(t),y(t) и z(t) сост. реш-е ур-е дв-е в виде ДУ т. обр. решить задачу механическим означ: 1)получить вид ур-я дв-я мех. сис-мы. 2)решить эти ур-я, что бы получ. зав. корд. от времени. Положен. Матер. (.)в данный момент времени опред. с пом. µ конец рад. при дв-е мат. (.) опис. в пр-ве кривую, наз. траекторией т. обр. Траектория-геом. место положения движения мат.(.) в опред. сис-ме отсчета. Инертность-свойство мат. тела сохр. сост-я покоя равн. или прямого действия. Инерц. СО – Со относит. к-ой мат.(.) движ. Равном и прямолинейном 2 СО наз. инерциал., если они движ. с Const скоростями.

2.Принцип относительности Галилея. Преобразования Галилея.

З-ны физики не зависят от выбора инерциальн. системы отсчёта. З-ны ньютона не завис от инерц со. V-скорость штриховой со , , . В случае, когда инерц. со и тело движ-ся с малой скоростью, скор-ти склад-ся лин образом. Преобразования Галилея: , , . Векторная ф-ма: . С и тоже самое. Движение одной со относ другой должн быть равным и прямолин. 2ой з-н Ньютона инвареантен(НЕИЗМЕН ОТНОСИТ ПРЕОБР ГАЛИЛЕЯ) 3ий относ одной к другой со.

Законы Ньютона. Методы решения задач в мех Ньютона.

1ый: Тело неподвижн дейст-ю силБ либо скомпенсир нах в сост покояю 2ой: Ускорение мат (.) прямопропорц силе и обратно пропорц её массе. 3ий: При взаимод 2ух тел. Сила действ одного тела на 2ое =силе противод(по модулю), но противоп по направлению и их действ. реал по прямой соед центры масс этих тел.