Геометрические и кинематические характеристики движения материальной точки
Геометрические и кинематические характеристики движения материальной точки
Механика изучает простейшую форму движения, т.е. перемещение одного тела относительно других.
Кинематика изучает движение, не интересуясь причинами его возникновения.
Материальной точкой наз. тело размерами которого можно пренебречь в условиях данной задачи.
Траектория - линия, описываемая мат. точкой в пространстве. Длина участка траектории пройдённого материальной точкой с момента начала отсчета наз. длиной пути. DS= DS(t). Вектор Dr= r- r0 , проведенный из начального положения движущейся точки в положение её в данный момент наз. перемещением. Вектором средней скорости наз. отношение приращения Dr радиуса-вектора точки к промежутку времени Dt.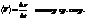 
мгновенная скорость есть векторная величина равная первой производной радиуса-вектора по времени модуль мгновенной скорости -
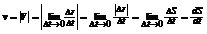
средняя скорость неравномерного движения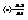 
длина пути за время D t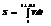 
Ускорение – быстрота изменения скорости по модулю и направлению.
Средним ускорением наз. векторная величина равная отношению изменения скорости DV к интервалу времени Dt -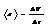 
Мгновенным ускорением мат. точки в момент времени t будет предел среднего ускорения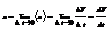 
Ускорение есть векторная величина равная первой производной скорости по времени.
Ускорение при криволинейном движении: нормальное, тангенциальное, полное.
Тангенциальная составляющая ускорения - характеризует быстроту изменения скорости по модулю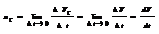 
Нормальная составляющая ускорения - направлена по нормали к центру кривизны - характеризует быстроту изменения скорости по направлению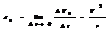 
Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих .
Вращательное движение тела. Векторы углового перемещения, угловой скорости и ускорения.
Угловой скоростью наз. векторная величина, равная первой производной угла поворота тела по времени.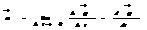 
Периодом вращения наз. время, за которое мат. точка совершает один полный оборот (2p)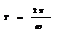 
Угловым ускорением наз. векторная величина равная первой производной скорости по времени.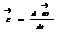 
При ускоренном движении вектор e сонаправлен w при замедленном противонаправлен.
Тангенциальная составляющая ускорения -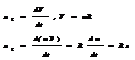 
Нормальная составляющая ускорения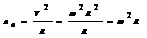 
Связь между угловыми и линейными характеристиками движения.
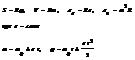
Силы гравитации, трения и упругости. Законы , которым подчиняются эти силы.
Различают 4 вида взаимодействий:
1. гравитационное 2. электромагнитное 3. ядерное 4. слабое (распад эл. част.)
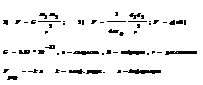
Внешним трением наз. трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном движении. Различают трение скольжения и трение качения.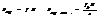 
где r радиус катящегося тела.
Связь момента импульса с моментом инерции
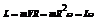
Идеальный газ
диаметр молекул <<< размеров сосуда
молекулы не взаимодействуют друг с другом
столкновения молекул упруги (V=const).
Параметры:
Температура – физ. величина, характеризующая состояние термодинамического равновесия макроскопической системы
Давление. Объём.
Закон Бойля-Мариота – для данной массы газа при постоянной температуре произведение давления газа на его объём есть величина постоянная. PV=const.
Закон Гей-Люссака –
1/ объём данной массы газа при постоянном давлении изменяется линейно с температурой
V=V0 (1+at)
2/ давление данной массы газа изменяется линейно с температурой p=p0 (1+at)
Геометрические и кинематические характеристики движения материальной точки
Механика изучает простейшую форму движения, т.е. перемещение одного тела относительно других.
Кинематика изучает движение, не интересуясь причинами его возникновения.
Материальной точкой наз. тело размерами которого можно пренебречь в условиях данной задачи.
Траектория - линия, описываемая мат. точкой в пространстве. Длина участка траектории пройдённого материальной точкой с момента начала отсчета наз. длиной пути. DS= DS(t). Вектор Dr= r- r0 , проведенный из начального положения движущейся точки в положение её в данный момент наз. перемещением. Вектором средней скорости наз. отношение приращения Dr радиуса-вектора точки к промежутку времени Dt.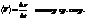
мгновенная скорость есть векторная величина равная первой производной радиуса-вектора по времени модуль мгновенной скорости -
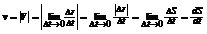
средняя скорость неравномерного движения 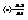длина пути за время D t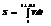
Ускорение – быстрота изменения скорости по модулю и направлению.
Средним ускорением наз. векторная величина равная отношению изменения скорости DV к интервалу времени Dt -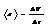
Мгновенным ускорением мат. точки в момент времени t будет предел среднего ускорения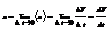
Ускорение есть векторная величина равная первой производной скорости по времени.