Измерительные приборы и электрические

ИЗМЕРЕНИЯ.

ЛЕКЦИЯ 11. ОБЩИЕ СВЕДЕНИЯ О СРЕДСТВАХ

ИЗМЕРЕНИЙ

Средства измерений - это технические средства, используемые при измерениях и имеющие нормированные метрологические характеристики. От средств измерений зависит правильное определение значения измеряемой величины. Поэтому в рамках темы 3 будут рассмотрены классификация средств измерений, применяемых в области электротехники, основные метрологические характеристики, принцип построения и работы измерительных приборов.

1. КЛАССИФИКАЦИЯ СРЕДСТВ ИЗМЕРЕНИЙ

Многообразие средств приводит к многоступенчатой классификации (рис. 11.1). На первой ступени все средства разделяются на два класса: по функциональному назначению и по выполняемым метрологическим функциям.

По выполняемым метрологическим функциям все средства делятся на эталоны, образцовые и рабочие средства. Эталоны – это средства измерений, предназначенные для хранения, воспроизведения и передачи размеров единиц физических величин рабочим средствам. Различают первичные эталоны, эталоны-копии, эталоны сравнения и рабочие эталоны.

Первичные эталоны воспроизводят размеры единиц физических величин с наивысшей точностью, достижимой в данной области измерений. Первичные эталоны, принятые в стране в качестве исходных, называются государственными эталонами.

Эталоны - копии предназначены для передачи размера единиц физических величин рабочим эталонам, которые служат для поверки и калибровки образцовых и наиболее точных рабочих средств измерений.

Эталоны сравнения предназначены для взаимного сличения.

Деление средств по функциональному назначению – это вторая ступень классификации. На этой ступени все средства делятся по пяти признакам: меры, измерительные преобразователи, измерительные приборы, измерительные установки и измерительно-вычислительные средства.

По количеству воспроизводимых значений единиц физических величин меры разделяют однозначные и многозначные. К однозначным мерам относят измерительные катушки сопротивлений, катушки индуктивностей, измерительные конденсаторы постоянной емкости, нормальные элементы и стабилизированные источники питания. К многозначным мерам относят измерительные генераторы, калибраторы напряжения, тока и фазового сдвига, измерительные конденсаторы переменной емкости, вариометры, магазины сопротивлений, индуктивностей, емкостей.

Деление измерительных преобразователей приведено на рис. 11.1. Первичными преобразователями называются датчики электрических сигналов. Они преобразуют значение физической величины (температуры, давления, размера и т. п.) в пропорциональное изменение параметра электрического сигнала (напряжения, тока, фазы). Такие преобразования значительно расширяют область применения электроизмерительных приборов, делая их универсальными средствами измерений

Масштабным называют измерительный преобразователь, предназначенный для изменения измеряемой величины в заданное число раз. К ним относят шунты, делители напряжения, измерительные усилители и измерительные трансформаторы.

Аналоговые преобразователи применяют для преобразования одной величины (например, мощности или напряжения) в другую (например, в частоту), более удобную для измерения. Аналого-цифровые (АЦП) и цифро-аналоговые (ЦАП) преобразователи широко применяются в устройствах и системах цифровой обработки сигналов.

Измерительной установкой называют совокупность функционально и конструктивно объединенных средств измерений и вспомогательных средств для рациональной организации измерений.

Измерительно-вычислительные (процессорные) средства включают в свой состав:

измерительно-информационные системы (ИИС) – совокупность функционально объединенных измерительных, вычислительных и вспомогательных средств для получения измерительной информации;

измерительно-вычислительные комплексы (ИВК) – совокупность автоматизированных средств измерений и свободно программируемой ЭВМ, которая обрабатывает результаты измерений, управляет процессом измерения и воздействует на объект.

Многообразие измерительных приборов требует ввести третью ступень классификации. Все измерительные приборы делят по пяти признакам:

– по виду сигнала измерительной информации,

– по способу представления информации,

– по измеряемой величине,

– по мобильности,

– по способу защиты.

Состав групп приборов, выделенных по каждому из перечисленных признаков, приведен на рис. 11.1 и не требует дополнительных пояснений. Однако необходимо отметить, что многообразие используемых в измерительных приборах сигналов измерительной информации стало причиной еще одной, четвертой ступени классификации.

На четвертой ступени все приборы разделяют на аналоговые и цифровые. Следует отметить, что класс цифровых измерительных приборов достаточно широк. Он разделяется по способу преобразования аналоговой величины в цифровой код, по измеряемой физической величине, по значению измеряемого параметра, по области применения и т. д.

2. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ИЗМЕРИТЕЛЬНЫХ

ПРИБОРОВ

На циферблаты, щитки и корпуса измерительных приборов наносятся обозначения, определяющие назначение прибора, тип измерительного механизма, род тока, класс точности, рабочее положение и др. Рассмотрим каждую из групп условных обозначений.

Условные обозначения, определяющие назначение приборов, сведены в таблицу 11.1. Таблица представляет три признака обозначения:

– род измеряемой величины,

– наименование прибора,

– условное обозначение.

Необходимо понимать, что в одной таблице невозможно даже перечислить все существующие в настоящее время измерительные приборы, поэтому в ней представлены только наиболее распространенные.

Таблица 11.1 .

Род измеряемой величины	Наименование прибора	Условное обозначение
Сила тока Напряжение Мощность Энергия Количество электрич. Сдвиг фаз Частота Сопротивление Индуктивность Емкость	Амперметр Вольтметр Ваттметр Счетчик киловатт-часов Счетчик ампер-часов Фазометр Частотомер Омметр Генриметр Фарадометр	А V W КWh Ah φ Hz Ω H F

В таблице 11.2 приведены условные обозначения класса точности, рабочего положения и внешних электрических контактов. Предварительно уточним, что класс точности измерительного прибора – это обобщенная характеристика, определяемая пределами основных допускаемых погрешностей.

Предел основной допускаемой погрешности обычно выражается:

– в единицах измеряемой величины, одним числом

∆_{п. пред} = ± а,

где ∆_{п. пред} – предел допускаемой абсолютной погрешности,

– в относительной величине (относительная погрешность),

,

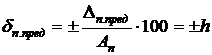где Ап – показания прибора,

– в приведенной величине (приведенная погрешность)

,

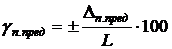где L – нормирующая величина.

Величина L равна:

– конечному значению рабочей части шкалы прибора, если нулевая отметка находится на краю шкалы,

– арифметической сумме конечных значений шкалы, если нулевая отметка находится внутри рабочей части шкалы,

– всей длине логарифмической или гиперболической шкалы.

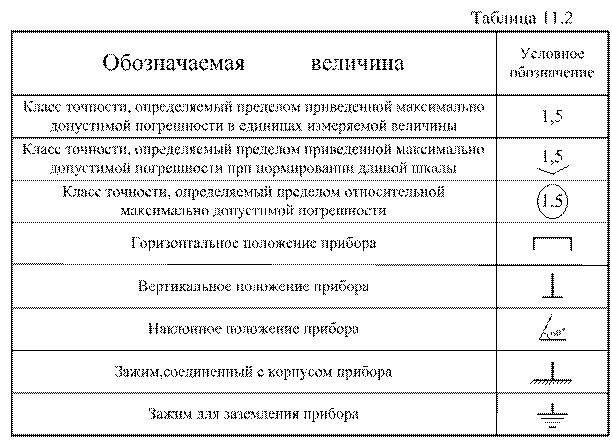
Условные обозначения типов измерительных механизмов приведены в

таблице 11.3.

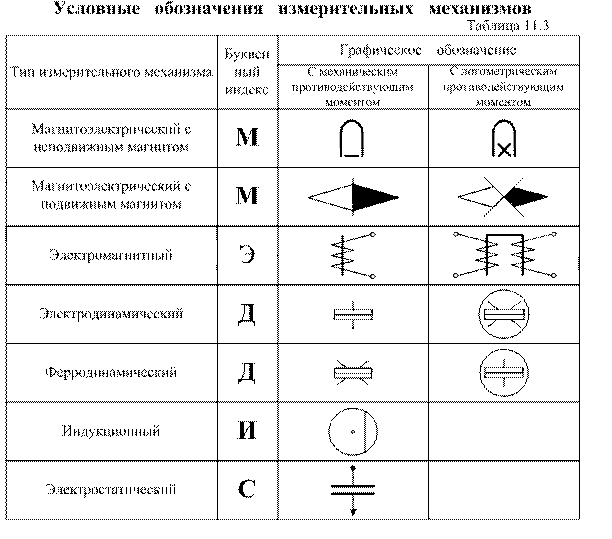
Рассмотренные условные обозначения дают достаточно полное представление об измерительном приборе. Кроме них на шкалу прибора

наносится заводское обозначение. Оно включает:

– буквенное обозначение типа измерительного механизма;

– обозначение завода изготовителя (одной или двумя цифрами);

– номер конструкторской разработки – цифрой.

3. ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ

Несмотря на разнообразие, средства измерений имеют некоторые общие свойства. Это позволяет сопоставлять их между собой. Свойства средств измерений описывают комплексом метрологических характеристик. В лекции рассмотрим основные характеристики.

Функция преобразования (статическая характеристика прибора). Она устанавливает функциональную зависимость между информативными параметрами входного и выходного сигналов средства измерений.

Чувствительность средства измерений – отношение приращения выходного сигнала 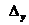к приращению входного сигнала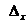

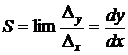. (11.1)

Если статическая характеристика преобразования нелинейная, то чувствительность зависит от х. Если статическая характеристика линейная, то чувствительность постоянна. У измерительных приборов с постоянной чувствительностью шкала равномерная, т.е. длина всех делений шкалы одинакова.

Величина, обратная чувствительности, называется постоянной прибора – С, причем

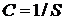. (11.2)

Порог чувствительности – наименьшее изменение входной величины, обнаруживаемое данным средством измерений.

Диапазон измерений – область значений измеряемой величины, для которой погрешность измерений не превышает установленных норм. Диапазон измерений может быть разбит на поддиапазоны.

Диапазон показаний – область значений шкалы, ограниченная начальной и конечной отметкой.

Цена деления шкалы – величина, определяемая разностью значений двух соседних отметок шкалы. Для цифровых измерительных приборов указывают цену единицы младшего разряда.

Полное входное сопротивление Z_вх – определяет мощность, потребляемую средством измерения от объекта.

Полное выходное сопротивление Z_вых средства измерения характеризует допустимую нагрузку на измерительный прибор.

Погрешности средств измерений. Совокупность погрешностей средств разделяют на приведенные, относительные и абсолютные; основные и дополнительные; систематические и случайные; аддитивные и мультипликативные; погрешности типа и экземпляра измерительного средства.

Динамическая характеристика – определяет инерционные свойства прибора.

Сведения о метрологических характеристиках приводятся в технической документации на средства измерения. Наиболее важные характеристики указывают на самих приборах.

Установление номинальных значений и границ допускаемых отклонений реальных метрологических характеристик средств от их номинальных значений называется нормированием метрологических характеристик.

4. СИГНАЛЫ ИЗМЕРИТЕЛЬНОЙ ИНФОРМАЦИИ

В средствах измерений передача, хранение и отображение информации о значениях измеряемых величин осуществляется посредством сигналов. Их принято называть сигналами измерительной информации. Любой сигнал определяется рядом параметров. Один из параметров сигнала измерительной информации функционально связан с измеряемой величиной. Такой параметр называют информативным. Рассмотрим основные виды сигналов, используемых в средствах измерений (рис. 11.2).

На рис.11.2, а пунктирной линией показан график изменения во времени измеряемой величины А. Сплошными линиями показан закон изменения сигналов измерительной информации. На остальных графиках пунктирная линия показывает закон изменения первичного электрического сигнала.

1. Сигналы, непрерывные (аналоговые) по информативному параметру и во времени. К таким сигналам относятся постоянные (рис. 11.2, а) или гармонические (рис.11.2, б, в, г) токи и напряжения.

Для постоянных токов и напряжений информативными параметрами являются их мгновенные значения I(t), U(t), функционально связанные с измеряемой величиной А зависимостью I(t) = K_I·A(t) или U(t) = K_U·A(t) ,где К_I, К_U – коэффициенты преобразования (рис. 11.2, а).

В гармонических сигналах информативными параметрами могут быть максимальная амплитуда U_m (амплитудное значение), угловая частота 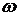или начальная фаза 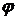. Изменение информативного параметра в соответствии с измеряемой величиной называют модуляцией сигнала. Соответственно информативным параметрам, различают амплитудную, частотную или фазовую модуляции (рис. 11.2, б, в, г).

2. Сигналы непрерывные по информативному параметру и дискретные во времени (рис. 11.2, д). Такие сигналы представляют последовательность значений информативного параметра, определимых в моменты t_i.

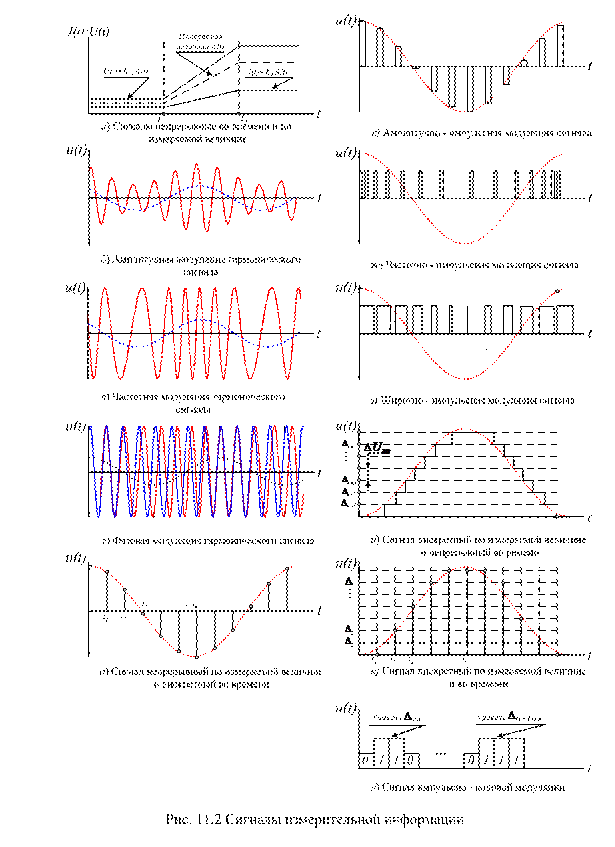
В реальных средствах это периодическая последовательность импульсов, у которых информативным параметром может быть амплитуда (рис. 11.2, е), частота (рис. 11.2, ж) или длительность (рис. 11.2, з) импульсов. В соответствии с этим различают амплитудно-импульсную (АИМ), частотно - импульсную (ЧИМ) и широтно-импульсную (ШИМ) модуляции.

3. Сигналы, непрерывные во времени и квантованные (дискретные) по

информативному параметру (уровню) приведены на рис. 11.2, и. Такие сигналы формируются на выходе ЦАП. Информативный параметр этих сигналов может принимать только разрешенные уровни (кванты) ∆_i.

4. Сигналы, дискретные во времени и по информативному параметру.

Теоретическая модель такого сигнала приведена на рис. 11.2, к.

Если каждому уровню такого сигнала поставить в соответствие кодовую комбинацию, то получим кодово-импульсную модуляцию (КИМ). Такие сигналы формируются на выходе АЦП (рис. 11.2, л).

5. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИГНАЛОВ

Под математической моделью понимают описание сигнала математическими выражениями (формулами, неравенствами, логическими соотношениями и т.п.). Общей особенностью всех моделей сигналов измерительной информации является априорная неопределенность значений информативных параметров. Подход к построению модели определяется классом сигнала. Рассмотрим подходы к построению моделей для квазидетерминированных и случайных сигналов.

Квазидетерминированными называются сигналы, закон изменения которых во времени известен, но не известен информативный параметр. Для построения модели таких сигналов используются как временные, так и спектральные представления. Например, скачкообразное изменение сигнала u(t) на выходе измерительного преобразователя можно описать функцией

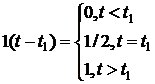. (11.3)

С помощью этой функции сигнал измерительной информации может

быть записан в виде

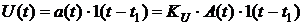. (11.4)

Для описания гармонических сигналов широко используют тригонометрические функции. Например, сигнал АМ имеет вид

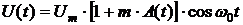, (11.5)

где m – коэффициент модуляции.

Для сигналов с АИМ математическая модель имеет вид

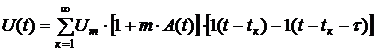, (11.6)

где 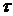- длительность импульсов.

Спектральное представление квазидетерминированных сигналов основано на преобразовании Фурье. Поэтому модель периодического сигнала u(t) имеет вид

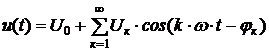, (11.7)

где U₀ – постоянная составляющая, U_к; 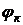- амплитуда и фаза к-ой гармоники, к – номер гармоники.

Для непериодического сигнала спектральное представление основано на применении интеграла Фурье

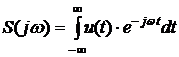. (11.8)

В общем случае сигналы измерительной информации – случайные процессы. Построение моделей таких сигналов основано на применении характеристик случайных процессов: закона распределения случайной величины, математического ожидания, среднего квадратического отклонения, корреляционной функции или спектральной плотности мощности.

КОНТРОЛЬНЫЕ ВОПРОСЫ

11.1. Перечислите основные признаки классификации средств измерений.

11.2. Чем отличаются рабочие средства измерений от эталонов?

11.3. Для чего предназначены аналоговые преобразователи?

11.4. По каким признакам разделяются измерительные преобразователи?

11.5. Приведите способы выражения предела основной допускаемой погрешности.

11.6. Приведите условное обозначение класса точности измерительного прибора, если для его определения использован предел относительной основной допускаемой погрешности.

11.7. Приведите условное обозначение класса точности измерительного прибора, если для его определения использован предел приведенной основной допускаемой погрешности, а нормирующая величина L выражается в единицах измеряемой величины.

11.8. Перечислите основные метрологические характеристики средств измерений.

11.9. В чем отличие постоянной средства измерения С от цены деления его шкалы?

11.10. Влияет ли полное входное сопротивление Z_вх средства измерений на значение погрешности измерений? Если влияет то почему?

11.11. Назовите основные классы сигналов измерительной информации.

11.12. Какой класс сигналов измерительной информации может быть использован в цифровых измерительных приборах?

11.13. Приведите определение математической модели сигналов измерительной информации.

11.14. Какой математической функцией описывают идеальный скачек сигнала измерительной информации?

11.15. Какие математические функции удобно применять для составления модели гармонических сигналов?

11.16. Применение каких характеристик может быть положено в основу построения модели случайных сигналов?